1 (Координаты в общем виде задаются совокуп­ностью трех символов символа оси (например, х), обозначения исходной точки (например, м) и обозначения конечной точки (например, w).

Опорные точки на траектории движе­ния инструмент позволяют представить эту траекторию как определенную по­следовательность точек, проходимых центром

инструмента (см. рис. 14.2) при обработке детали. Каждое из положений (каждая

опорная точка) в выбранной системе координат может быть опреде­лено числами,

например координатами. Сочетание таких чисел, определяющих ряд последовательных положений инст­румента, или, иначе, ряд опорных точек траектории, и будет представлять основ­ную часть программы работы станка, выраженную в числовом виде (см. рис 14.4) в другую осуществляется путем неслож­ного пересчета.

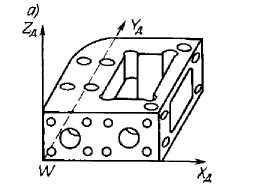
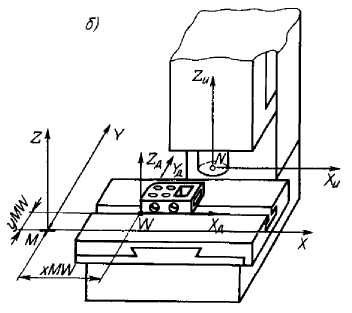
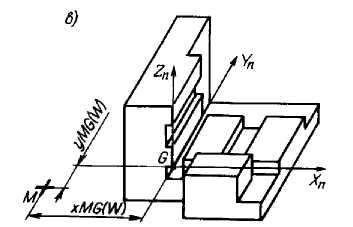
Рис. 14.5. Схема расположения детали на станке:

а - деталь в системе координат_детали; б - размещение детали на станке; в - система координат

Приспособления

В начале программирования в систе­ме координат детали X_ДY_ДZ_Д задают по­ложение базовых элементов заготовки (рис. 14.5, а). Относительно нуля детали (точка W) задаются при программирова­нии все опорные точки, определяющие траекторию движения центра инструмен­та при обработке.

При установке детали на станок (рис. 14. б) положение нуля детали (точки W) будет зафиксировано относи­тельно координатной системы станка XYZ координатами xMW, yMW, zMW.

Если при обработке детали использу­ют приспособление (рис. 14.5, в), то оно должно быть закоординировано на стан­ке относительно нуля станка (точки М). Система Z_иNX_и определяет координат­ную систему инструмента (см. рис 14.5, б). Естественно, что

при установке дета­ли в приспособлении координатная Рис. 14,6. Схемы задании

си­стема детали X_ДWY_Д, должна совпадать с координат опорных точек1-3 координатной системой приспособле­ния X_пGY_n. а - абсолютные размеры;

При обработке детали при движении по элементам б - размеры в приращениях

траекторий (прямым, ду­гам, кривым) в промежутках между опорными точками инструмент в определенных случаях может перемещаться по траектории, несколько отличающейся от заданной. Однако можно задать такое опорных точек, при котором отклонения от фактической граектории от требуеиой будет меньше некоторой наперед заданной величины и деталь будет об р а- ботана в пределах заданной точности.

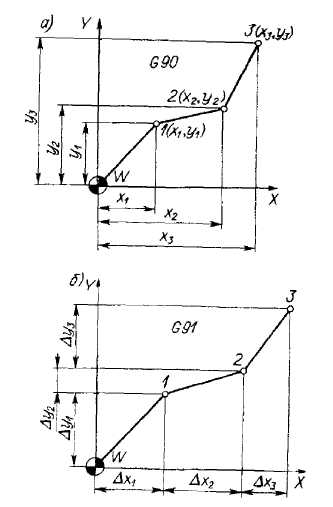
Таким образом, начальный этап представления траектории обработки детали связан прежде всего с получением координат_опорных точек траектории. Эти координаты могут быть выражены абсолютными размерами, т. е. для каждой опорной точки заданными относительно нулевой точки станка или детали (рис 14.6, а), или задаваться в виде прираще­ний в направлении движения инструмен­та от одной опорной точки к

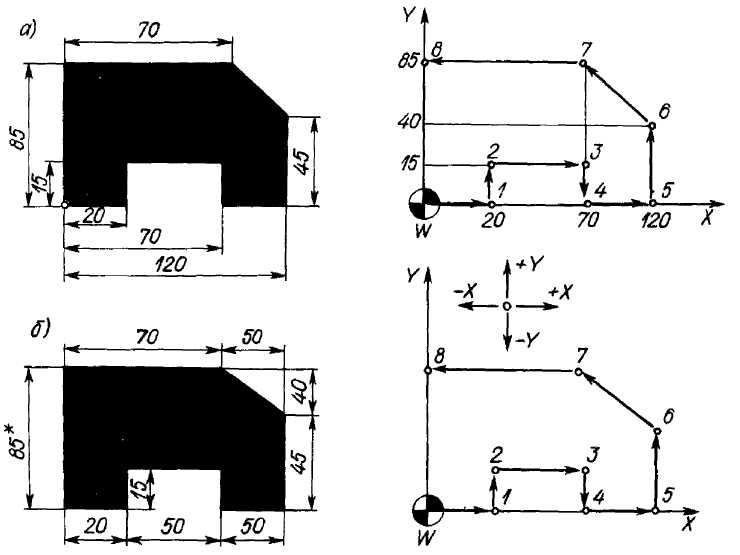
Рис. 1.21. Схемы задания размеров деталей:

а - абсолютные размеры (х, у); б - относитель­ные размеры (∆х, ∆у):

другой (рис. 14.6, б). При записи УП способ задания кодируется буквенно-цифровы­ми символами G90 (абсолютные коорди­наты) и G91 (размеры в приращениях). Так, при перемещении центра инструмен­та (рис. 14.6,б) из точки W в точку 1 координата х изменится на величину ∆x₁, а координата у - на величину ∆y₁; при дальнейшем движении из точки 1 в точ­ку 2 приращение по оси X составит ∆х₂, по оси Y - ∆y₂ т. д. Задание координа­тами точек траектории движения центра инструмента зависит во многом от способа_задания размеров детали (рис. 14.7).

В большинстве систем ЧПУ работой станка управляют дискретно, с помощью импульсов. Цена одного импульса (наи­меньшее программируемое перемеще­ние), или дискретность системы, отражает разрешающую_способность комплекса, включающего систему ЧПУ, механизм подач и датчики обратной связи. Исходя из дискретности системы приращения ко­ординат между опорными точками тра­ектории можно выразить не в мм, а коли­чеством импульсов. Например, если дискретность по оси X составляет 0,01 мм/имп., а по оси Y - 0,02 мм/имп., то значения ∆х и ∆у, равные, например, соответственно 12,85 мм и 8,6 мм, в им­пульсах будут выражены следующим образом: ∆х =1285 имп., ∆у = 430 имп.

Задание приращений по двум осям координат, однако, еще не определит заданного

прямолинейного движения инструмента между точками. Даже при постоянной скорости подачи по осям вследствие неравенства координат задан­ной точки (∆x₁≠∆y₁) время движения по оси X не будет равно времени движе­ния по оси У и заданная траектория будет искаженной (на рис. 14.8, а пока­зано штрихами). Как уже говорилось, приблизить фактическую траекторию к заданной можно введением дополнитель­ных (промежуточных) опорных точек (точки 2 - 5 на рис. 14.8,б) и заданием соответствующей последовательности пе­ремещений инструменту между этими точками, например: (∆х, ∆y); (2∆х); (2∆х, 2∆у); (∆х); (∆х, ∆.у), т. е. траекторию по сравнению с ранее определенной (см. рис. 14.8, а) приходится разбивать на более мелкие участки. Величина δ оп­ределит ошибку в отработке.

При программировании введение до­полнительных опорных точек приводит к резкому увеличению расчетов и объема программы. Поэтому в практике_детальное представление заданной траектории движения инструмента между двумя опорными точками (с выдачей команд на соответствующие перемещения по осям) осуществляется с помощью спе-циального вычислительного устройства - элемента УЧПУ - интерполятора. Ин­терполятор непрерывно, т. е. в каждый данный момент, в процессе перемещения (в соответствии с

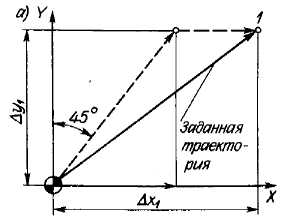
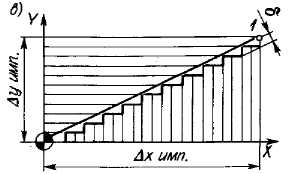
Рис. 14.8. Линейные траектории перемещения центра инструмента

заданными прираще­ниями) инструмента от одной опорной точки к другой поддерживает функцио­нальную связь между координатами опорных точек, т. е. обеспечивает отра­ботку траектории в зависимости от вида функции. Если функция выражает пря­мую линию, то отрабатываемая траекто­рия будет линейной, а интерполятор называется линейным. В процессе ра­боты такой интерполятор при исходных заданных приращениях ∆х₁, и ∆y₁ (см. рис. 14.8, а) непрерывно должен под­держивать такое соотношение скоростей движения инструмента по осям, при кото­ром инструмент будет перемещаться по заданной линейной траектории.

Обеспечить точно функциональную связь между движениями по осям коор­динат в каждой данной точке траекто­рии очень сложно. В большинстве су­ществующих станков перемещение инструмента, по заданной траектории осуществляется приближенно, путем вклю­чения подачи попеременно то вдоль од­ной, то вдоль другой оси. При этом интер­полятор системы управления непрерывно оценивает_отклонения от заданной траектории и стремится свести эти отклоне­ния к минимуму. Скачки ступенчатой траектории при формирований заданной незначительны. Они равны или кратны цене одного управляющего импульса, поступающего из интерполятора, или им­пульса, формируемого датчиком обрат­ной связи. Например, прямая наклонная линия может формироваться поперемен­ной подачей на приводы импульсов в такой последовательности: один импульс по оси Y и два импульса по оси X (рис. 14.8, в). Поскольку в современных стан­ках наиболее часто цена импульса прини­мается равной 0,001 мм, то перемещение между двумя соседними опорными точка­ми практически можно рассматривать как плавное. Интерполяция может быть также круговой, с помощью полиномов второй и высших степеней и др.

Работа интерполятора как вычисли­тельной машины основана на решении определенных задач. Известно несколько методов интерполяции, среди которых наиболее распространен метод оценоч­ной функций, основанный на решении алгебраических уравнений.

При линейной интерполяции отрезок прямой рассматривается в системе коор­динат, начало которой совмещено с на­чальной точкой Т_о интерполируемого от­резка T_оT_к (рис. 14.9, а). Оценочную функцию для любой из промежуточных точек T_i траектории вдоль прямой можно выразить формулой

F_ii = y_ix_k – x_iy_k (14.1)

где x_k, y_k - координаты конечной точки T_k интерполируемого отрезка; координа­ты начальной точки при интерполяции отрезка прямой равны нулю; x₁, у₁, - текущие координаты точки Т_i, траектории, определяемые числом элементарных ди­скретных перемещений i вдоль оси X и j вдоль оси У.

Логическая сущность оценочной фун­кции состоит в том, что для всех точек заданной прямой справедливо (рис. 14.9, а) соотношение y_k/x_k = y₁,/x₁, или у_кх_i = y₁х_к (14.2)

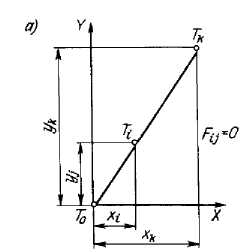
Рис. 14.9. Схемы к определению оценочной функции

Разность произведений yjx_k — y_kx_i = F_tj определит зону, где расположена точка. Естественно, что при F_ij,=0 точка находится на прямой, т. е. справедливо соотношение

(14.2). Если F_ij > 0, то точка находится выше прямой (например, у_i больше, чем требуется, или x_i меньше); при F_ij<0 точка находится (рис. 14.9, б) ниже прямой (например, у_i меньше, чем требуется, или х_i, больше). Таким обра­зом, можно считать, что интерполируе­мая прямая делит плоскость на две части: область F > 0, где оценочная функция после подстановки в нее коор­динат точек этой области принимает положительные значения, и область F<0, где значения оценочной функции отрицательны. Интерполятор определяет последовательность элементарных ди­скретных перемещений в зависимости от квадранта, в котором расположен ин­терполируемый отрезок. Для случая, когда отрезок находится в первом квад­ранте системы координат, направление элементарного дискретного перемещения определяется в зависимости от располо­жения предыдущей точки: если она нахо­дится в области F≥0, то дискретное перемещение осуществляется вдоль оси X, если в области F<0, то вдоль оси У. И так до тех пор, пока текущая точка траектории не совпадет с точкой конца интерполируемого отрезка.

В соответствии с принятым характе­ром перемещений интерполятор выдает попеременно импульсы управления то по одной, то по другой координате. Напри­мер (рис. 14.10, а), если из начальной точ­ки Т_о согласно поданному импульсу управления центр инструмента перемес­тился по траектории Т_о— 1, то интерпо­лятор, определив для координат точки 1 значение функции F_ij=y₁x_k = y_kx₁<0, следующие импульсы будет подавать в цепь управления приводом подач станка по оси У. После подачи каждого импуль­са интерполятор определяет значение оценочной функции. Как только после по­дачи очередного импульса оценочная функция (F_ii = y₂x_k — y_kx₁) изменится, т. е. станет либо равна нулю, либо больше нуля (в точке 2, рис. 14.10, а), интерполя­тор опять начнет выдавать импульсы для управления приводом перемещения по оси X, прекратив подачу импульсов в привод управления перемещением по оси У (рис. 14.10,6). В точке 3 значение F_tl=y₂x_k — у_кх_з станет меньше нуля и интерполятор обеспечит движение к точ­ке 4, выдавая импульсы в привод пере­мещения по У. И так далее для всего отрезка от точки Т_о до точки Т_к Следует иметь в виду, что количество импульсов на отрезке перемещения от точки к точке зависит от дискретности системы УЧПУ. При круговой интерполяции начало системы координат совмещается с цент­ром окружности радиуса R (рис. 14.11, а). Оценочная функция для любой из про­межуточных

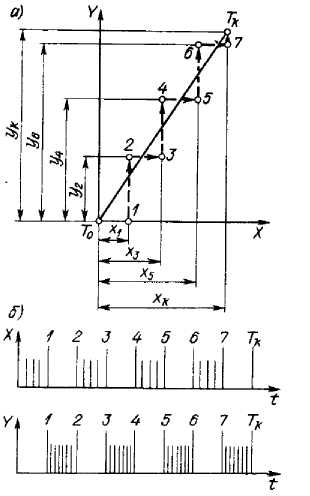
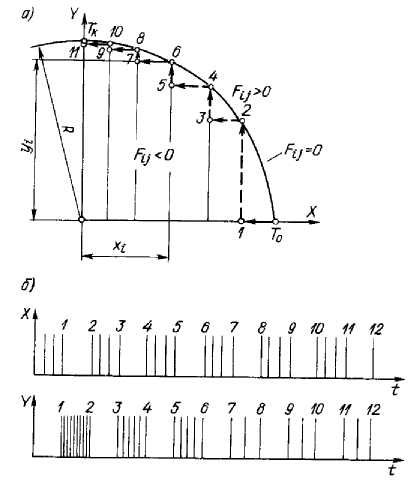
Рис. 14.10. Линейная интерполяция Рис. 14.11. Круговая интерполяция:

по методу оценочной функции: а - схема траектории; б - схема подачи

а - схема траектории; б - схема подачи импульсов по осям X и Y

импульсов по осям X и Y

точек траектории вдоль ок­ружности выражается формулой F_ii = х_i²+ у²_j – R². Формула получена из со­отношения х_i²+ у²_j = R², справедливого для точек, лежащих на дуге.

Окружность делит плоскость на две части: область F > 0, расположенную вне окружности, и область F <0, находя­щуюся внутри нее. В зависимости от направления движения вдоль окруж­ности (по или против часовой стрелки) и квадранта расположения интерполи­руемой дуги выбирается правило опре­деления последовательности элементар­ных дискретных перемещений. Для иллю­стрируемого случая проверяется положе­ние текущей точки: если F≥0, дискрет­ное перемещение осуществляется в от­рицательном направлении оси X, а если F<0 - в положительном направлении оси Y. Интерполяция начинается в точ­ке Т_о и продолжается до тех пор, пока не будет достигнута точка T_k дуги окруж­ности или граница квадранта. Выполняя работу, интерполятор соответственно на­правляет импульсы в привод подач то по X, то по Y (рис. 14.11, б).

Аппроксимация дуг окружностей. На станках с ЧПУ, снабженных лишь линейными интерполяторами, програм­мирование обработки деталей затрудне­но, если траектории выражены дугами окружностей и кривыми другого порядка. Дуги окружностей для ввода информа­ции в УЧПУ с линейным интерполятором аппроксимируют ломаными линиями с вве­дением по дуге определенного числа опорных точек (рис. 14.12). Величина элементарных участков между точка­ми - участков аппроксимации - зави­сит от углового шага ∆φ - централь­ного угла дуги, которую заменяют дордой, секущей или касательной.

Угловой шаг ∆φ, а следовательно, и число опорных точек на дуге зависят при заданном

Рис. 14.12. Линейная аппроксимации радиусе R от принимаемого значения стрелки

дуги окружности прогиба б, определяю­щей точность

аппроксимации, т. е. сте­пень приближения ломаной линии к дуге окружности. Естественно, что чем меньше значение принятого углового шага, тем ближе обработанный контур будет по форме приближаться к круговому (заданному). Но при программировании следует учитывать что уменьшение б приводит к увеличению расчетных работ и объема программы| из-за увеличения числа

опорных точек. Угловой шаг для заданного радиуса и назначенной величины δ можно опре­делить или расчетом, или по таблицам, или ориентировочно по графикам. При выборе углового шага следует учитывать характер траектории инструмента. Для облегчения расчетов при аппроксимиро­вании следует использовать специальные таблицы.

В современных условиях большинство станков с ЧПУ оснащены УЧПУ с линейно_-круговыми интерполяторами, поэтому заниматься вопросами аппроксимации дуг окружностей технологу-программи­сту приходится сравнительно редко. Эти задачи встречаются в настоящее время лишь при расчётах по апроксимации кривых второго порядка.

При программировании обработки кроме определения величины перемеще­ния центра инструмента по траектории необходимо указать скорости перемеще­ния инструмента между отдельными опорными точками, целый ряд вспомо­гательных технологических команд и др. Все это оформляется в виде расчетно-технологической карты (РТК) на обра­ботку данной детали и карты кодирова­ния программы.

В общем случае для составления УП необходимо иметь операционный эскиз детали, чертеж заготовки и РТК, допол­ненную таблицей координат опорных точек или расстояний между точками (приращений).

Подготовительные функции. Функции c адресом G, называемые подготовитель-ными, определяют режим и условия ра­боты станка и УЧПУ. Они кодируются от G00 до G99. За каждой из функций закреплено стандартом определенное значение (табл. 14.1). В конкретных УЧПУ значение тех или иных функций может отличаться от рекомендуемых стандар­том, это оговаривается конкретной мето­дикой программирования. В общем под­готовительные функции можно разграни­чить на несколько гpynn:

GOO, . .., G09 - команды общего по­рядка: позиционирование, линейная или круговая интерполяция, ускорение, за­медление, пауза (выдержка);

G10, . .., G39 - особенности непре­рывной обработки: выбор осей, плоско­стей, видов интерполяции;

Таблица 14.1.