2˚. Физические приложения кратных интегралов.

Массу тела можно найти по формуле , где объёмная плотность материала, массу пластины − по формуле (на этот раз − поверхностная плотность). Точно так же, заряд можно вычислить, интегрируя объёмную (поверхностную) плотность распределения заряда.

Центр масс: , здесь − снова масса тела .

Напряженность в точке гравитационного поля, создаваемого массой, распределённой с плотностью , равна , где − гравитационная постоянная. Потенциал гравитационного поля равен .

Моменты инерции: , , и т.д.

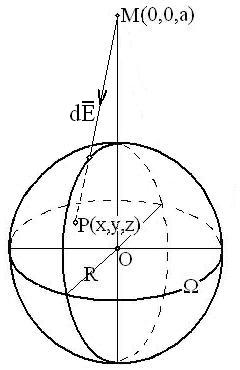
Пример. Доказать, что однородный шар притягивает материальную точку, находящуюся вне шара, так, как если бы вся масса шара была сосредоточена в его центре.

Решение. Если расположить шар и точку так, как показано на рисунке, будет . Вычислим , считая, что .

. Сделаем во внутреннем интеграле следующую замену: . При этом будет , ; . , где − масса шара.

Понятие о несобственных кратных интегралах*.

Мы не станем здесь углубляться в теорию, а рассмотрим лишь один пример: .

Мы можем определить его как предел частичного интеграла разными способами. Например,

или .

1. = .Следовательно, .

2. Так как подынтегральная функция положительна, то интеграл возрастает с расширением области.

Поэтому . Следовательно, . Воспользуемся этим, результатом для вычисления интеграла Пуассона .

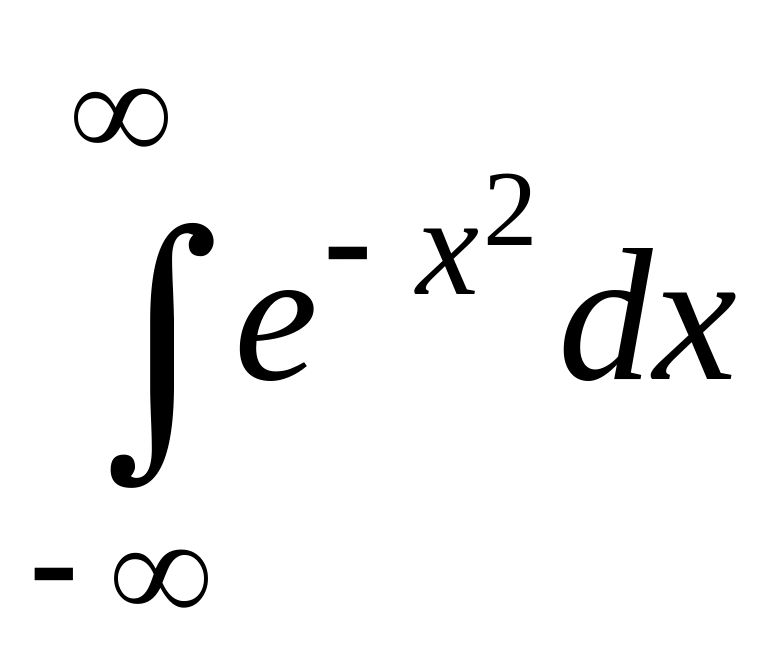Имеем 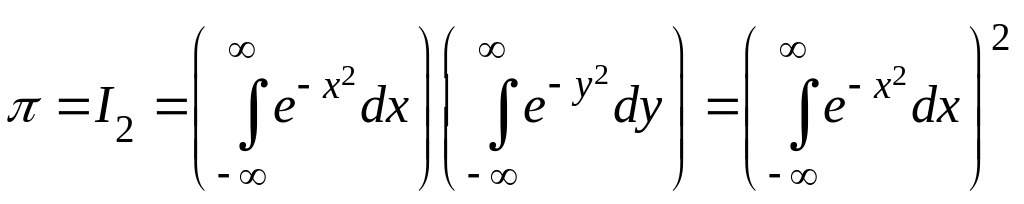. Поэтому .

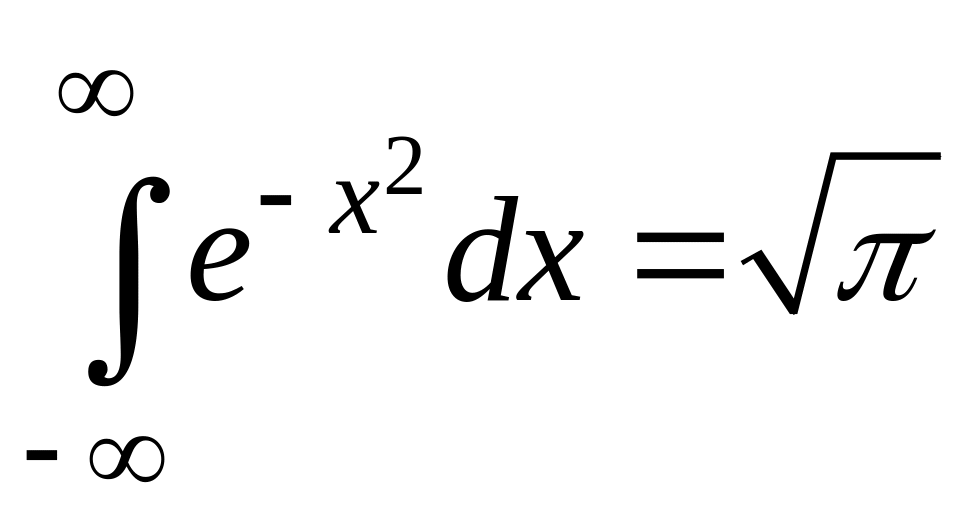Отметим, что для теории вероятностей и других дисциплин важным является следствие этой формулы .

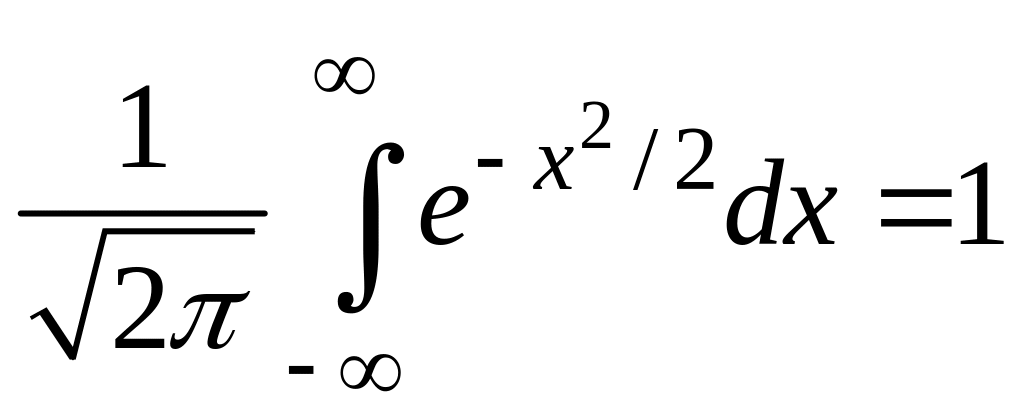Формула Грина (связь криволинейного интеграла на плоскости с двойным).

1˚. Криволинейный интеграл по координатам.

Пусть − кривая, заданная параметрическими уравнениями 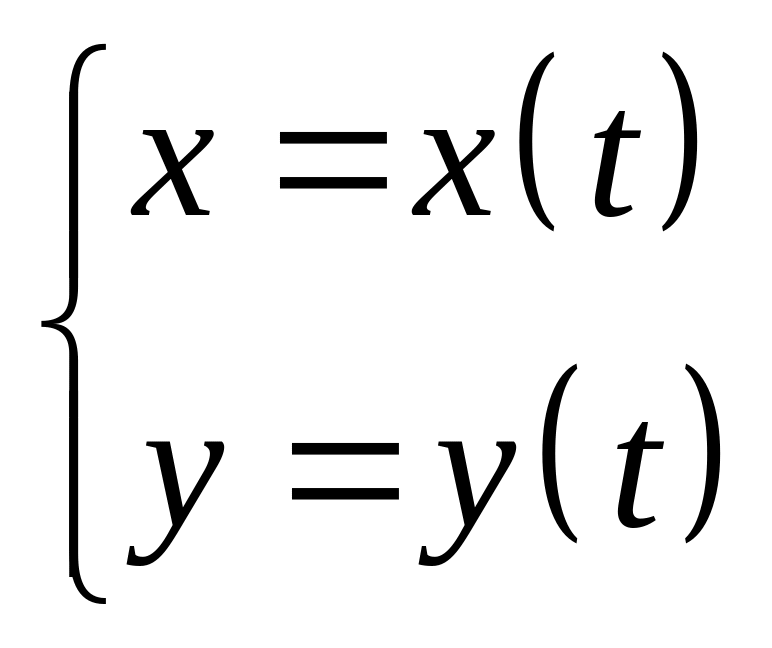, ; и пусть − функции, определенные в точках этой кривой. Рассмотрим разбиение отрезка точками , выберем промежуточные значения и обозначим току кривой с координатами . Составим интегральную сумму 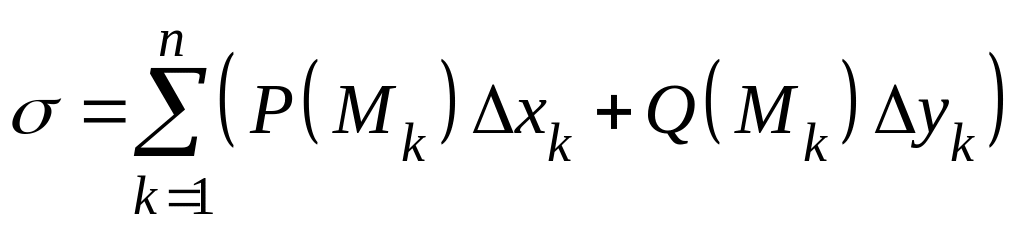(здесь , а и т.д.).

Определение. Если существует предел , где , то он называется криволинейным интегралом по координатам и обозначается .

Для вычисления криволинейного интеграла следует превратить его в определённый интеграл с помощью “замены переменной”. Точнее, справедлива

Теорема. Если − гладкая кривая, а функции непрерывны вдоль этой кривой, то существует криволинейный интеграл, при этом 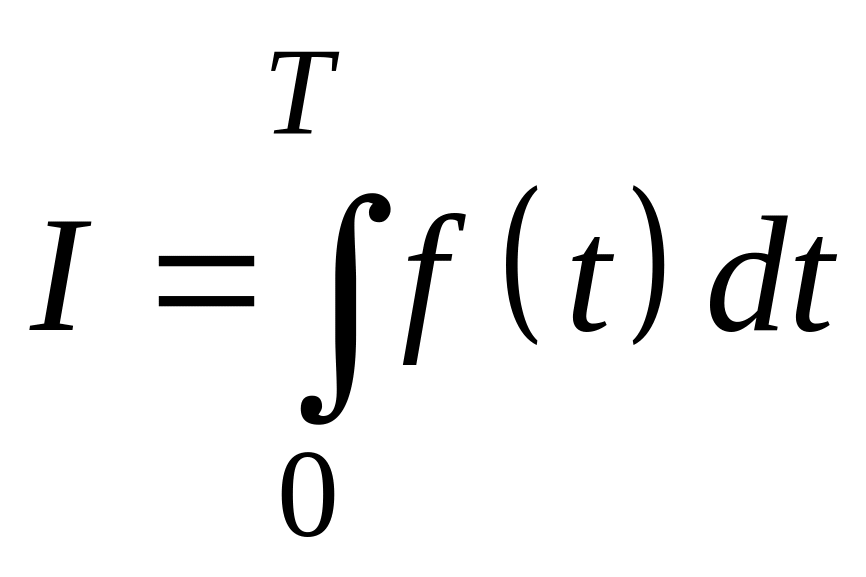, где .

Помимо обычных свойств интеграла, вроде аддитивности по дуге и линейности, справедливо ещё одно: интеграл вдоль границы области, является аддитивной функции самой области.

Поясним формулировку нового свойства рисунком. В изображенной на рисунке конфигурации интегралы по дугам AB и BA взаимно уничтожатся.

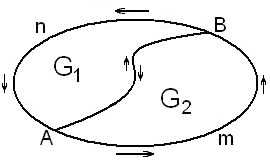
Формула Грина.

Теорема. Пусть − область на плоскости , граница которой − замкнутая кусочно-гладкая кривая, и пусть функции и непрерывно дифференцируемы в замкнутой области . В таком случае справедливо равенство:

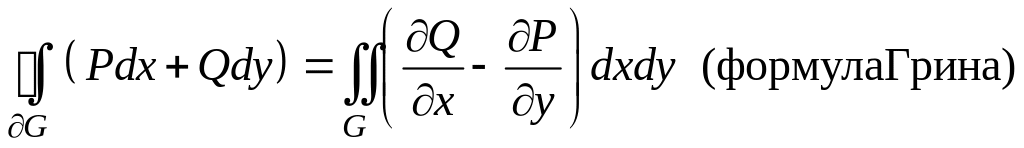. (1) Здесь означает интегрирование вдоль замкнутой кривой, которая обходится против направления движения часовой стрелки.

Доказательство.

1. Выведем сначала формулу (1) в том случае, когда область является простой (т.е. сечения области координатными прямыми содержат не более одного отрезка).

а) Так как простая, то.

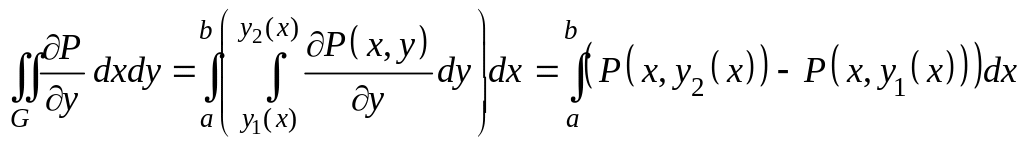
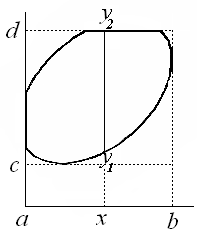
С другой стороны, 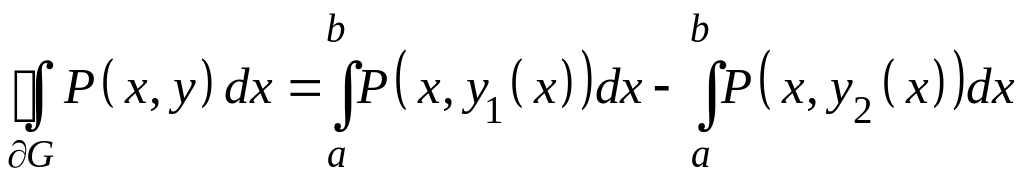. Следовательно, .

б) Точно так же доказывается, что . Складывая два полученных равенства, приходим к формуле (1).

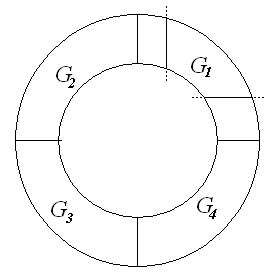
2. Покажем на примере кругового кольца , что формула Грина верна и для областей, которые можно разбить на несколько простых областей.

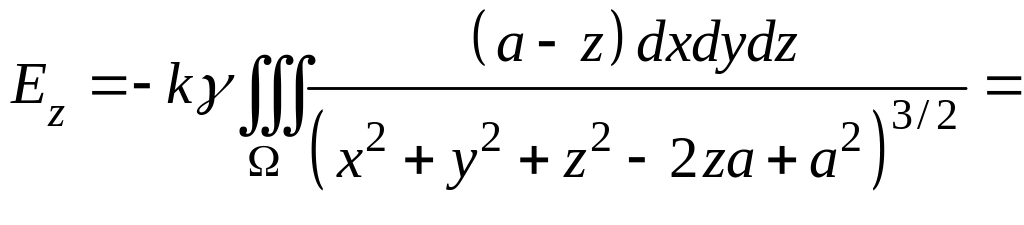
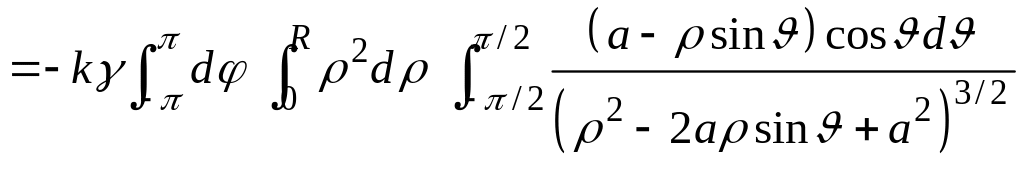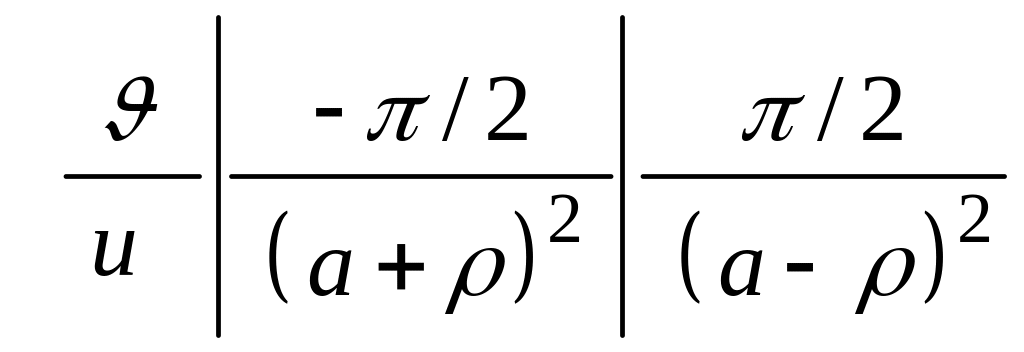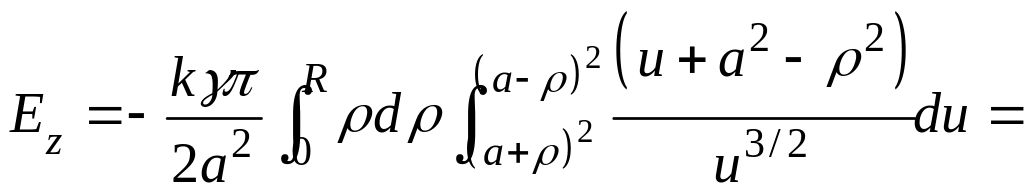
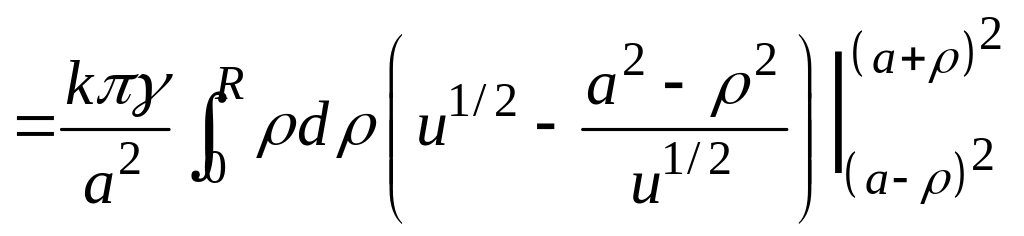
Каждая из частей , на которые разрезано кольцо, является простой, поэтому , . Сложим эти четыре равенства. Сумма левых частей равна . 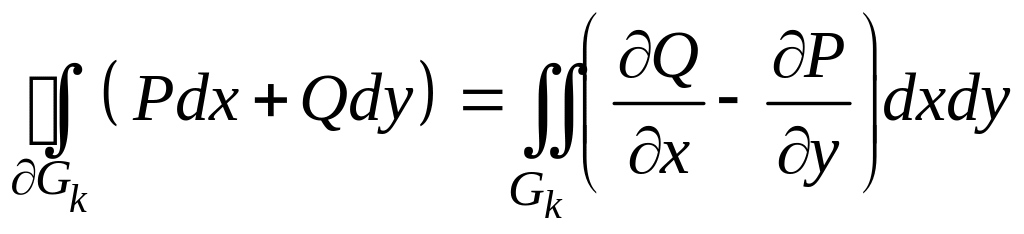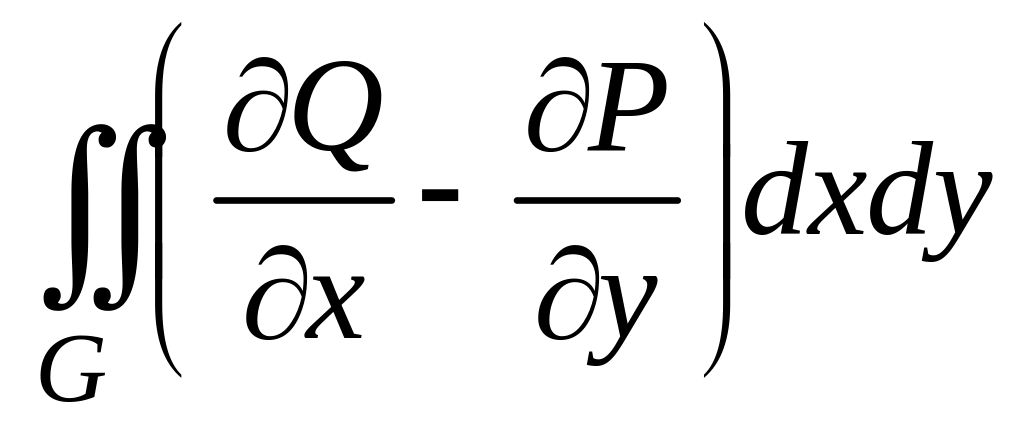Сумма правых частей равна . Это показывает, что формула Грина верна для кольца .