Тройной интеграл.

1º. Мера Жордана в пространстве .

Рассмотрим разбиение пространства на кубы ранга с помощью плоскостей , , , . Обозначим количество кубов ранга, содержащихся во множестве и − количество кубов ранга, пересекающихся с множеством . Пусть ещё .

Определение. Внутренней мерой Жордана множества называется величина . Внешней мерой Жордана множества называется величина . Множество называется измеримым по Жордану или кубируемым, если . Их общее значение называется просто мерой этого множества или его объёмом.

2º. Определение тройного интеграла. Пусть − кубируемое, ограниченное множество и − функция, определенная на этом множестве. Рассмотрим разбиение на неперекрывающиеся кубируемые подмножества и выберем точки . Обозначим − объём множества и диаметр этого множества. Назовем мелкостью разбиения величину . Образуем интегральную сумму Римана .

Определение. Если существует предел , то функция называется интегрируемой по Риману на множестве , в записи − , а сам предел называется тройным интегралом и обозначается или .

Точно так же, как в одномерном и двумерном случаях, формулируются и доказываются критерий интегрируемости, теорема о существования тройного интеграла от непрерывной функции и основные свойства интеграла. Отметим только, что средним интегральным в трёхмерном случае называют величину

.

Замечание. По той же схеме определяется мера Жордана и интеграл в пространстве при любом натуральном .

3º. Сведение кратных интегралов к повторным интегралам.

Пусть , ; − сечение множества гиперплоскостью и пусть − проекция на подпространство (т.е. на подпространство первых координат).

Теорема. Пусть существует интеграл и пусть при любом значении существует интеграл по сечению . В таком случае существует повторный интеграл . При этом .

Отметим частные случаи, когда : 1) и 2) .

Замена переменных в кратных интегралах.

1˚. Перед тем как сформулировать правило замены переменных в кратных интегралах, напомним это правило в одномерном случае.

Рассмотрим гладкое отображение (замену переменной) . Будем считать, что , причём не обращается в нуль на отрезке . Пусть еще , . Тогда .

Теорема. Пусть − область с кусочно-гладкой границей и , где , − взаимно однозначное отображение класса , причем якобиан этого отображения 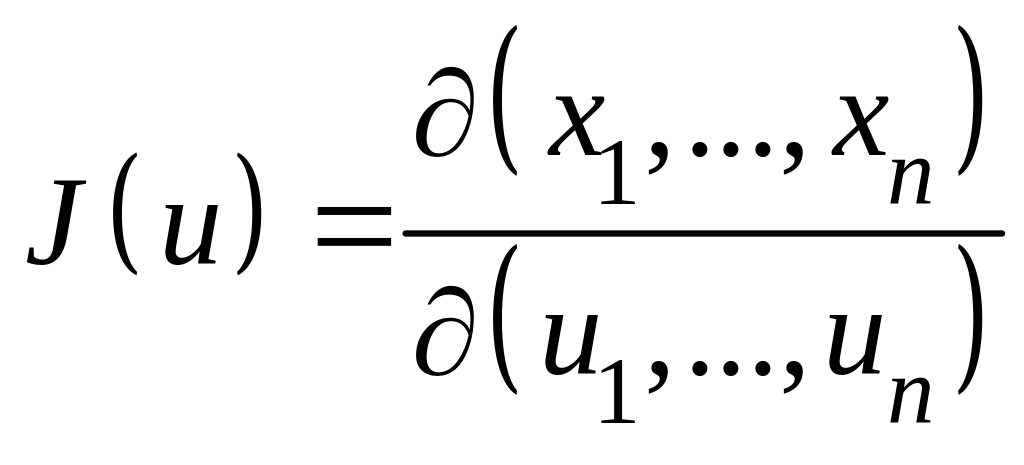не обращается в нуль в области . Пусть ещё . Тогда

.

Эту формулу можно объяснить следующим образом. Из линейной алгебры известно, что , где − линейный оператор , показывает, во сколько раз изменяется объём любого параллелепипеда (и, значит, любого тела) под действием оператора . Отсюда нетрудно вывести, что модуль определителя Якоби отображения представляет собой коэффициент искажения объёма бесконечно малой окрестности точки под действием этого отображения.

2˚. Криволинейные координаты в области задаются с помощью гладкого взаимно однозначного отображения , для которого якобиан не обращается в нуль . Координатной линией называются образ линии , вдоль которой изменяется только координата .

В качестве примера криволинейных координат рассмотрим полярные координаты на плоскости. В этом случае − полярный радиус точки , отсчитываемый от полюса O, − полярный угол, отсчитываемый от полярной оси. Если , − координаты точки в правой прямоугольной декартовой системе координат, где ось совпадает с полярной осью, то . Линии − лучи, выходящие из точки , линии − окружности с центром в этой точке.

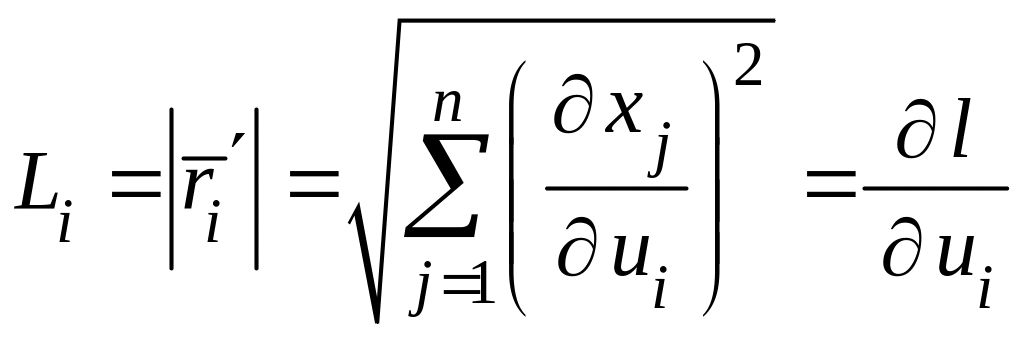Вернёмся к общему случаю. По касательной к линии в заданной точке идёт вектор , который мы будем коротко записывать . Длина этого вектора называется коэффициентом Ламэ и обозначается . По предыдущему , т.е. − коэффициент искажения длины вдоль линии . В таком случае − единичный касательный вектор к линии . Набор векторов называется подвижным репером. Он, вообще говоря, зависит от точки, в которой вычислены все эти векторы. Если подвижный репер в каждой точке образует ортогональную систему векторов, то криволинейные координаты называются ортогональными.

Имеем . В ортогональном случае из этой формулы, в частности, следует, что

.

Таким образом, в случае перехода от прямоугольных декартовых координат к ортогональным криволинейным координатам коэффициент искажения объёма равен произведению коэффициентов искажения длины вдоль координатных направлений.