
- •Раздел 2 Линейные измерительные системы 19
- •Розділ 1.Теоретичні основи вимірювально-інформаційних систем.
- •Основні поняття
- •Вимірювальні сигнали та їхні пеетворення
- •Методичні похибки інформаційних систем
- •Раздел 2 Линейные измерительные системы
- •2.1.Волновые уравнения
- •2.2 Метод нелинейного преобразования времени
- •2.3 Взаимодействие волны с неподвижной границей раздела
- •2.4.Взаимодействие волны с подвижной границей разделa
Раздел 2 Линейные измерительные системы
2.1.Волновые уравнения
Рассмотрим жидкую идеальную сжимаемую среду. Система уравнений гидродинамики , описывающее изоэнтропическое движение среды включает уравнение движения, уравнение неразрывности и уравнение состояния

 (2.1)
(2.1)

где
 -
плотность;
-
плотность;
P- давление;
 -
вектор скорости;
-
вектор скорости;
 оператор
Гамильтона;
оператор
Гамильтона;
div- оператор дивергенции.
Если среда является сплошной и однородной, уравнение состояния принимает вид
 для
жидкости; (2.2)
для
жидкости; (2.2)
 -
для газа,
(2.3)
-
для газа,
(2.3)
где
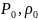 -параметры
невозмущенной среды;
-параметры
невозмущенной среды;
 ,n,
,n, -константы.
-константы.
Полагая движение среды потенциальным, введем в рассмотрение потенциал скоростей

Введем обозначения
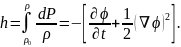 (2.4)
(2.4)
Для жидкости, учитывая уравнения состояния (2.2), получим:
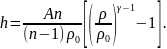 (2.5)
(2.5)
Для газа, с учетом (2.3)
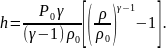 (2.6)
(2.6)
Давление в жидкости при известном потенциале скоростей определяется выражением
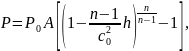 (2.7)
(2.7)
где
 -
невозмущенная скорость звука, равная
-
невозмущенная скорость звука, равная
 -
для
жидкости;
-
для
жидкости;
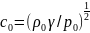 -
для газа.
-
для газа.
Для скорости звука получим следующее представление , исходя из выражения
c=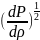 .
.
Для жидкости
 .
(2.8)
.
(2.8)
Для газа
 .
(2.9)
.
(2.9)
Можно показать, что система уравнений (2.1), (2.2) эквивалентна нелинейному волновому уравнению в классе потенциальных течений среды
 (2.10)
(2.10)
Используя представление (2.8) для скорости звука, уравнение (2.10) преобразуем к виду
 .
(2.11)
.
(2.11)
Если в уравнении (2.10) ограничиться удержанием квадратичной нелинейности, то последнее следует записать в виде
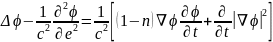 .
(2.12)
.
(2.12)
Представляет интерес волновое уравнение с местной скоростью звука, которое получается из (2.11) отбрасыванием правой части
 .
(2.13)
.
(2.13)
Уравнение (2.13) эквивалентно уравнению вида
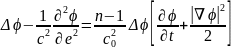 .
(2.14)
.
(2.14)
Уравнение (2.14) похоже на уравнение (2.12), но, с одной стороны, оно содержит член с кубической нелинейностью, а, с другой стороны, в нем отсутствует один из членов с квадратической нелинейностью.
При последовательной линеаризации нелинейного уравнения (2.10) вводится малый параметр
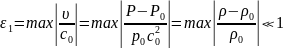 (2.15)
(2.15)
При этом уравнение (2.7) и (2.10) распадаются на рекуррентную систему
 (
2.16)
(
2.16)
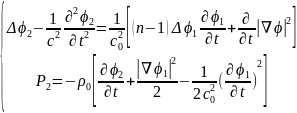 (2.17)
(2.17)
В дальнейшем ограничимся рассмотрением симметричных волновых движений акустической среды.
 ,
,
где v=0,1,2;

Отметим, что устремляя в любом из волновых уравнений скорость звука к бесконечности, получим уравнение Лапласа, описывающее движение несжимаемой среды.
2.2 Метод нелинейного преобразования времени
Рассмотрим генерирование волн давления нестационарно движущимся в сжимаемой жидкости (акустической среде) плоским поршнем. Конструктивно это может быть достигнуто движением поршня в трубе. Полагаем, что скорость движения поршня достаточно мала по сравнению со скоростью звука в среде, так что квадратом этого отношения по сравнению с единицей можно пренебречь. Однако, полагаем, что перемещения поршня значительны настолько, что граничное условие необходимо задавать на текущем положении возмущающей границы. С учетом сказанного математическую постановку задачи запишем в виде
 (2.18)
(2.18)
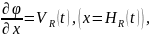 (2.19)
(2.19)
где
 -
потенциал скоростей возмущенного
движения среды,
-
потенциал скоростей возмущенного
движения среды,
х - координата,
t - время,
С0 - скорость звука в среде,
 -
скорость движения поршня;
-
скорость движения поршня;
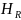 -закон
движения поршня, но в общем случае
-закон
движения поршня, но в общем случае
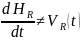 .
.
Начальные условия полагаем нулевыми, т.е. полагаем
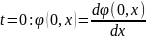 (2.20)
(2.20)
При
известном потенциале скоростей
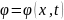 скорость
среды и давление в среде определяются
выражениями
скорость
среды и давление в среде определяются
выражениями
Рис.
2.1. Плоский поршень в трубе с жидкостью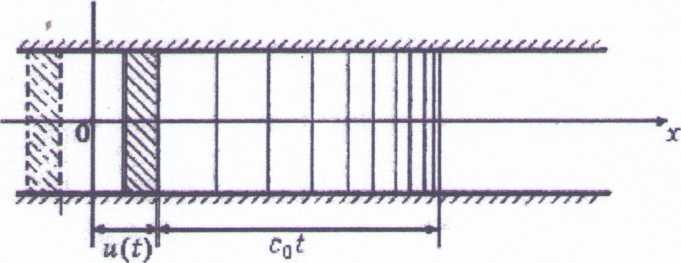
 ,
(2.21)
,
(2.21)
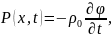 (2.22)
(2.22)
где р0 - плотность среды.
Решение поставленной задачи (2.18)- (2.22) будем искать методом нелинейного преобразования времени. В соответствии с этим методом решение волнового уравнения (2.18) запишем в виде
 (2.23)
(2.23)
 ,
(2.24)
,
(2.24)
где
 - волновой аргумент (
- волновой аргумент ( ),
),
Р - неизвестная (искомая) функция волнового аргумента, определяемая из граничного условия (2.19).
Подставляя решение (2.23) в граничные условия (2.19), получаем соотношение вида
 (2.25)
(2.25)
Для решения уравнения (2.25) воспользуемся преобразованием времени
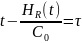 (2.26)
(2.26)
исходя из которого получаем обратную функцию
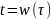 (2.27)
(2.27)
где -время.
-время.
Заметим,
что преобразование вида (2.26), (2.27) лежит
в основе метода нелинейного преобразования
времени, как метода решения волновых
задач с подвижными границами. При
условии, что функция НR
(t)
является
однозначной
и непрерывной и при выполнении неравенства
 можно
утверждать, что обращение (2.27) однозначно.
можно
утверждать, что обращение (2.27) однозначно.
С учетом преобразования (2.26), (2.27) уравнение (2.28) принимает вид
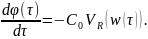 (2.28)
(2.28)
Интегрируя
уравнение (2.28) по
 ,
получаем
,
получаем
 (2.29)
(2.29)
Учитывая,
что решение волнового уравнения должно
быть функцией волнового аргумента в
(2.19) принимаем
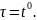 Тогда
получаем решение краевой задачи в виде
Тогда
получаем решение краевой задачи в виде
 (2.30)
(2.30)
Скорость среды и давления в среде находим в виде
V(x,t)= (2.31)
(2.31)
Остановимся
на определении обратной функции из
соотношения (2.26). В ряде случаев задания
закона H(t)
обратное преобразование (2.27) можно
получить из решения алгебраического
уравнения (2.26). Например, пусть
 Тогда
Тогда
 и
и ,
,
где
М0
=
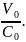
Если
функция
 представлена в виде степенного ряда,
то
представлена в виде степенного ряда,
то
решение уравнения (2.27) проводится в соответствии с формулами обращения степенных рядов. Так, если
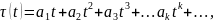 (2.32)
(2.32)
 (2.33)
(2.33)
При этом преобразовании коэффициенты ряда (2.32) определяются по формуле
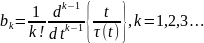 (2.34)
(2.34)
Наконец, при выполнении условия можно воспользоваться методом последовательных приближений

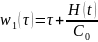 ,
(2.35)
,
(2.35)

Аналогичным образом находятся последующие приближения. В большинстве случаев практики можно ограничиться первым приближением.
