1.6. Результат работы программы (Python).
Вывод версии интерпретатора:
$ python -V
Python 2.7.3
Собственно, тестирование программы:
$ ./prime.py Primality test.
Enter natural number: 131071 Nunber 131071 is prime $ ./prime.py Primality test.
Enter natural number: 123 Nunber 123 is composite
1.7. Текст программы (Ruby). Напишем программу ещё на одном крайне популярном интерпретируемом языке Ruby:
#!/usr/bin/env ruby
def is_prime(n)
return (n != 1) && !(2..Math.sqrt(n).round).any?{|i| n % i == 0} end
puts "Проверка простоты числа."
print
"Введите
натуральное
число:
" a = gets.chomp.to_i if (a <= 0)
raise "assert(a > 0)" end
puts "Число #{a} - " + (is_prime(a) ? "простое" : "составное")
По умолчанию Ruby не поддерживает assert-ы, поэтому мы проводим явную проверку корректности аргумента.
1.8. Результат работы программы (Ruby).
$ ruby -v
ruby 1.8.7 (2011-06-30 patchlevel 352) [x86_64-linux]
$ ./prime.rb
Проверка простоты числа.
Введите натуральное число: 131071 Число 131071 - простое $ ./prime.rb
Проверка простоты числа.
Введите натуральное число: 123
Число 123 – составное.
Задача 2 (4). Даны натуральные числа m и n. Определить их наибольший общий делитель nod.
2.1. Постановка задачи. Наибольшим общим делителем двух целых чисел называется наибольший из их общих делителей. Для ненулевых чисел наибольший общий делитель единственен.
Существует широко известный алгоритм определения наибольшего общего делителя двух чисел, так называемый алгоритм Евклида. Его мы и реализуем.
2.2. Алгоритм. Код программы зачастую существенно упрощается, если использовать рекурсию, то есть вызов функции из самой себя с изменёнными аргументами. К сожалению блок–схема алгоритма в этом случае усложняется. Блок– схема основной части программы:
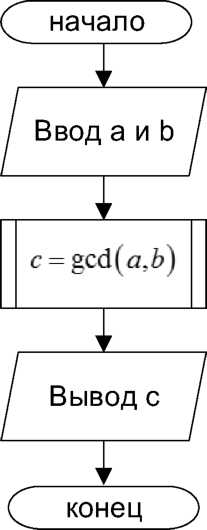
Блок–схема
функции с = gcd (a, b):
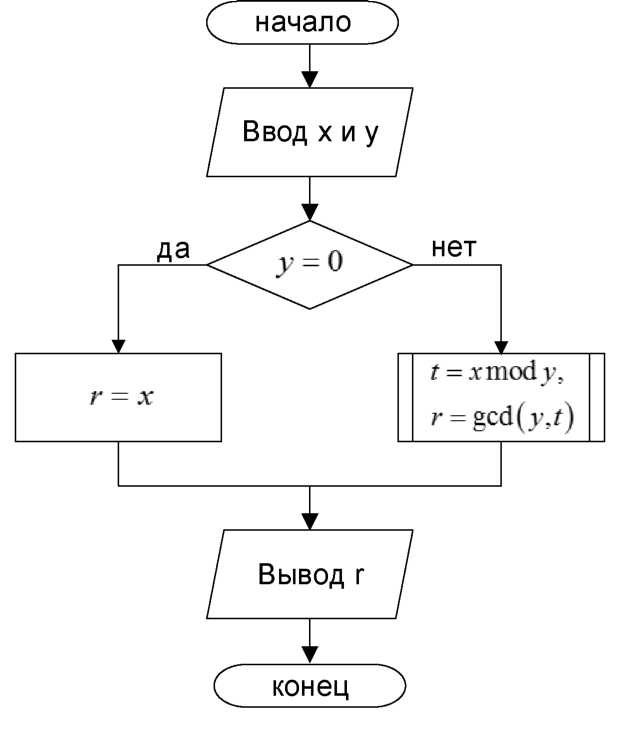
2.3. Текст программы (C++).
#include <iostream>
#include <assert.h>
static int gcd(const int x, const int y) {
return (y == 0) ? x : gcd(y, x % y);}
int main() {
std::cout << "Нахождение наибольшего общего делителя чисел a и b." << std::endl;
std::cout << "Введите число a: "; int a;
std::cin >> a; assert(a > 0);
std::cout << "Введите число b: "; int b;
std::cin >> b; assert(b > 0);
const
int c = gcd(a, b);
std::cout << "НОД(а,Ь) = " << мНОД(" << a << << b << ") = " << c <<
std::endl;
return 0;}
2.4. Результат работы программы (C++).
$ g++ -o gcd ./gcd.cpp $ ./gcd
Нахождение наибольшего общего делителя чисел а и b.
Введите число a: 3817 Введите число b: 5899 НОД^,^ = НОД(3817,5899) = 347
В данном случае 3817= 347*11 и 5899= 347*17.
2.5. Текст программы (Python).
#!/usr/bin/env python
def gcd(x, y): return x if y == 0 else gcd(y, x % y)
if name == " main ":
print "Greatest common divisor for a and b." try:
a = int(input('Enter a: ')) assert(a > 0)
b = int(input('Enter b: ')) assert(b > 0)
c = gcd(a, b)
print "GCD(a,b) = GCD({0},{1}) = {2}".format(str(a),str(b),str(c))
except Exception as e: print "Error: {0}".format(str(e))
2.6. Результат работы программы (Python).
$ python -V Python 2.7.3 $ ./gcd.py
Greatest common divisor for a and b.
Enter a: 347*11 Enter b: 347*17
GCD(a,b) = GCD(3817,5899) = 347
Видно, что мы вводили вместо чисел математические выражения, Python сам вычислил соответствующие значения выражений.
2.7.
Текст программы (Ruby).
#!/usr/bin/env ruby
def gcd(x,y)
return (y == 0) ? x : gcd(y, x % y) end
puts "Нахождение наибольшего общего делителя чисел a и b."
print "Введите число a: " a = eval(gets.chomp).to_i if (a <= 0)
raise "assert(a > 0)" end
print "Введите число b: " b = eval(gets.chomp).to_i if (b <= 0)
raise "assert(b > 0)" end
c = gcd(a,b)
puts "НОД^,^ = НОД^^},#^}) = #{c}"
2.8. Результат работы программы (Ruby).
$ ruby -v
ruby 1.8.7 (2011-06-30 patchlevel 352) [x86_64-linux]
$ ./gcd.rb
Нахождение наибольшего общего делителя чисел a и b.
Введите число a: 347*11
Введите число b: 347*17
НОД^,^ = НОД(3817,5899) = 347