Нейрон и его модели

Одиночный нейрон принимает возбуждения от огромного количе­ства нейронов (их число может достигать несколько тысяч). Считается, что мозг че­ловека состоит из порядка 10¹¹ нейронов, которые имеют между собой примерно 10¹⁵ соединений. Каждый нейрон передает возбуждение дру­гим нейронам через нервные стыки, называемые синапсами, при этом процесс передачи сигналов имеет сложную электрохимическую природу. Синапсы играют роль репитеров информации, в результате функциони­рования которых возбуждение может усиливаться или ослабляться. Как следствие, к нейрону приходят сигналы, одна часть из которых оказыва­ет возбуждающее, а вторая - тормозящее воздействие. Нейрон суммиру­ет возбуждающие и тормозящие импульсы. Если их алгебраическая сум­ма превышает некоторое пороговое значение, то сигнал с выхода нейро­на пересылается посредством аксона к другим нейронам.

Рассмотрим модель нейрона, связанную с первыми попытками формализовать описание функционирования нервной клетки. Введем следующие обозначения:

u₁…., u_N - входные сигналы данного нейрона, приходящие от дру­гих нейронов;

w_1…., w_N - синаптические веса;

у - выходной сигнал нейрона;

v- пороговое значение.

Формула, описывающая функционирование нейрона, имеет вид:

Формула описывает модель нейрона, представленную на рис. 5. Эта модель была предложена МакКаллоком и Питтсом в 1943 году.

Рис. 5. Модель нейрона МакКаллока и Питтса.

И данная модель может быть представлена в виде:

где

а также w₀ = v, u₀ = 1.

В качестве функции f может приниматься не только единичная функция (a), но и другие пороговые функции:

или

или

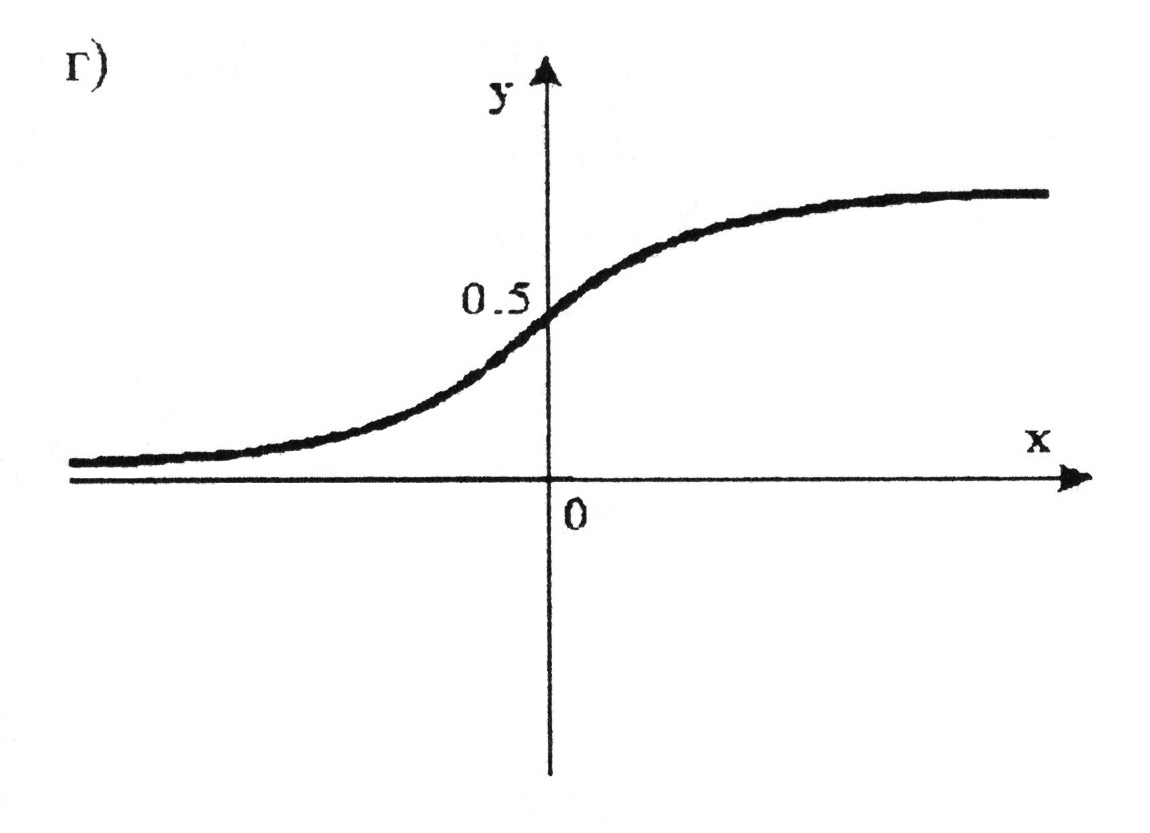
или

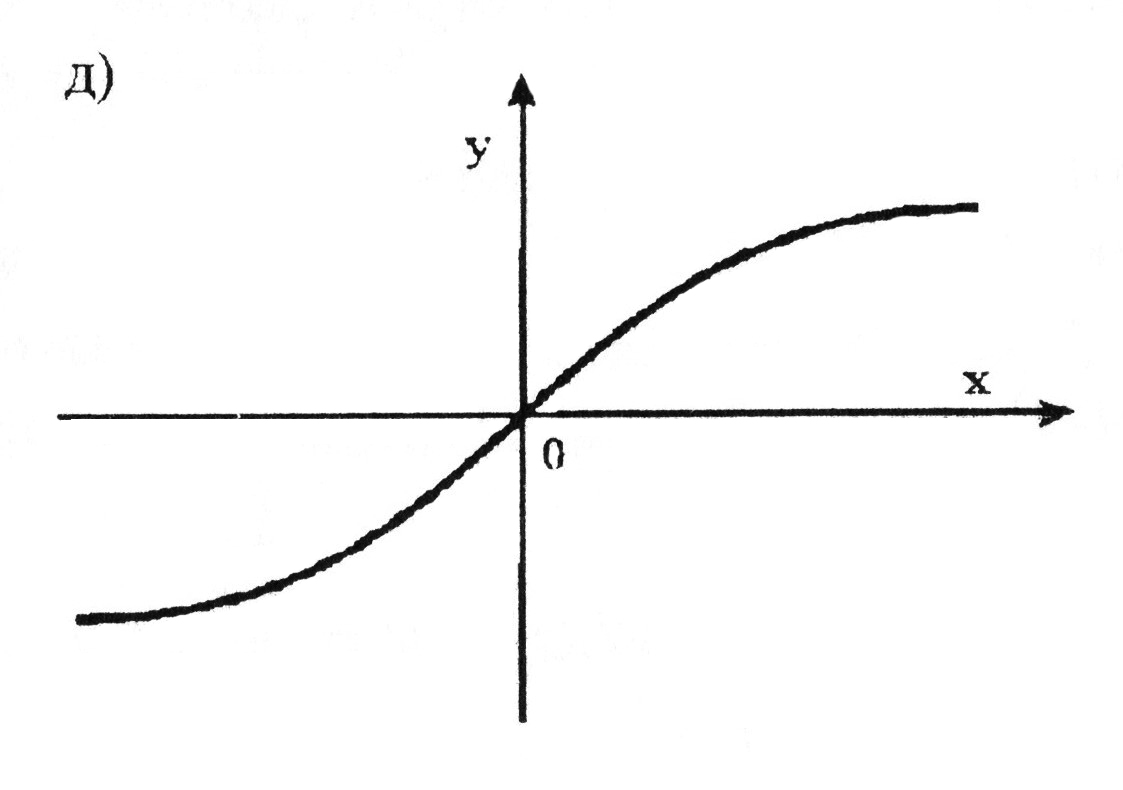
Рис. 6. Примеры функции f.

Примеры а,б,в,г,д соответствуют приведенным формулам.

На начальной фазе моделирования биологических нейронных сетей применялись пороговые функции а, б и в. В настоящее время чаще всего используется сигмоидальная функция (г), характеристика которой при β→∞ стремится к пороговой униполярной функции (а). В качестве альтернативы применяется функция гиперболического тангенса (д). В этом случае ее характеристика стремится к пороговой биполярной функции при α→∞.

Модель МакКаллока-Питтса стала отправной точкой для построения простейшей однонаправленной нейронной сети, названной персептроном. Такую сеть предложил и исследовал Розенблатт в конце пятидесятых - начале шестидесятых годов XX века. На рис. 7 представлена структура персептрона, иногда называемого простейшим персептроном. В качестве функции f модели МакКаллока-Питтса применялась биполярная функция активации.

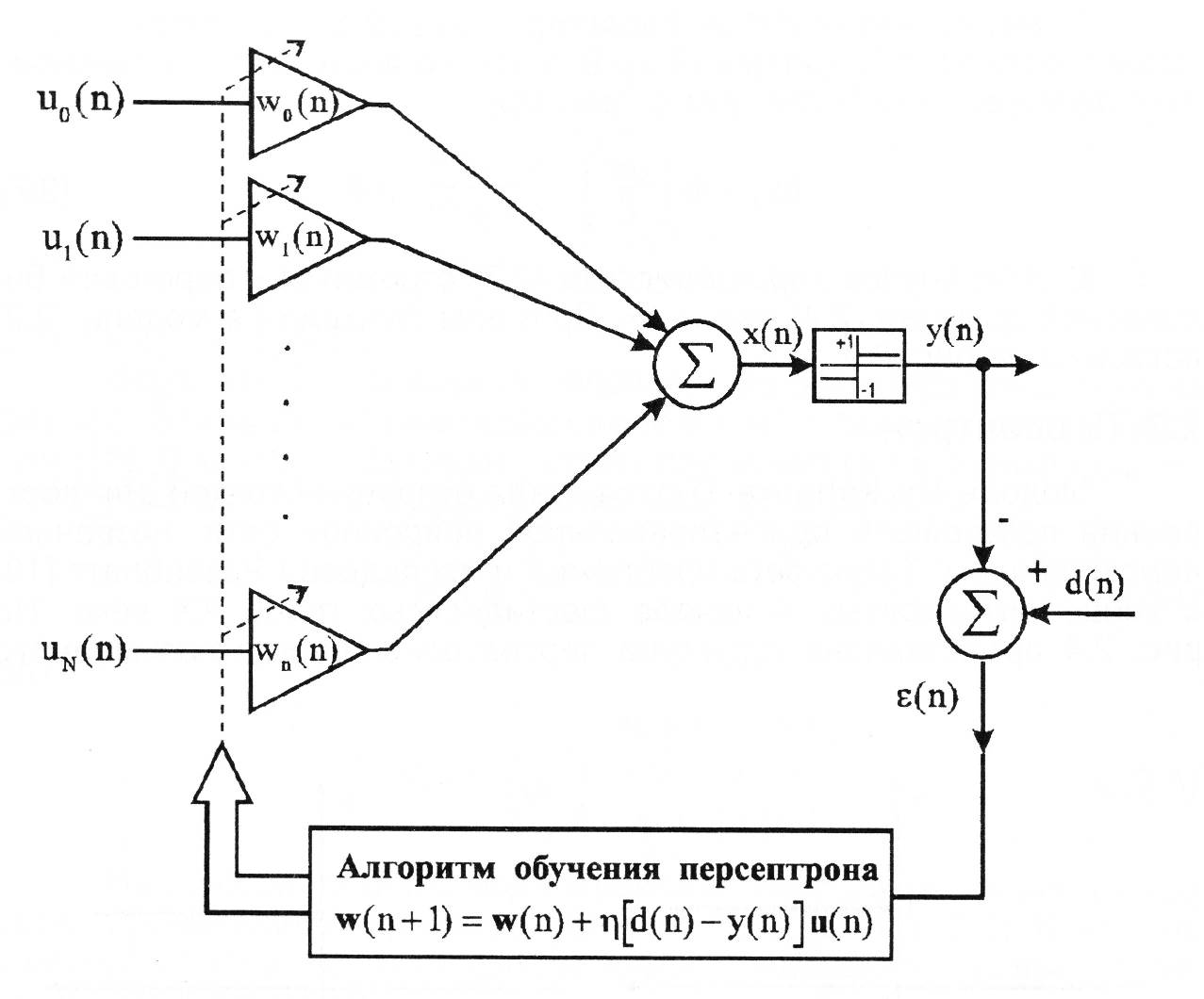
Рис. 7. Модель простейшей однонаправленной нейронной сети - персептрона.

Обучение персептрона заключается в рекуррентной коррекции вектора весов w(n) на основе произведения параметра коррекции η с погрешностью между эталонным сигналом d(n) и фактическим выходным сигналом y(n) на обучающей выборке u(n). Причем шаг коэффициента коррекции варьирует в пределах 0 < η < 1, тогда как начальные значения вектора весов устанавливаются равными нулю.

СПИСОК ЛИТЕРАТУРЫ

1. Адаптогены в медицинских и биологических системах (Теория и практика восстановительной медицины. Том III): Монография / Хадарцев А.А. [и др.]; науч. ред. А.А. Хадарцева и В.М. Еськова. - Тула: ООО РИФ «ИНФРА» - М., 2005.- 220 с.

2. Анохин, П.К. Узловые вопросы теории функциональной системы / П.К. Анохин. - М.: Наука, 1980. - 196 с.

3. Анфилатов, В.С. Системный анализ в управлении / В.С. Анфилатов, А.А. Кукушкин. - М.: Финансы и статистика, 2002.- 368 с.

4. Возможности управляющих воздействий на функциональные системы организма человека / под ред. А.А. Хадарцева и В.Э. Фризена. - Тула: ТулГУ, НИИ НМТ, 1999.- 208 с.

5. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. И. Д. Рудинского. - М.: Горячая линия -Телеком, 2007. - 452 с: ил.

6. Физиология человека: Учебник /Под ред. В.М.Покровского, Г.Ф.Коротько. - М.: Медицина. - 2000. - Т. - 448 с.