8. Частотні характеристики мінімально фазових ланок

Наведені в табл. 4 значення частотних характеристик ланок відносяться тільки до так званих мінімально фазових ланок. Мінімально фазовою є ланка, в якої всі нулі чисельника передаточної функції та полюси знаменника мають від’ємні або рівні нулю дійсні частини. Передатна функція будь-якої системи може бути представлена як відношення двох поліномів, а саме:

. (6.135)

Коренями передаточної функції є значення, при яких Передатна функція дорівнює нулю, це корені поліному U(p).

Полюсами передаточної функції э значення, при яких Передатна функція має значення, рівне безконечності. Такі значення вона має, коли знаменних дорівнює нулю. Тобто корені знаменника передаточної функції називаються її полюсами.

Ланки, в яких хоча б один корінь або полюс знаходиться в правій (додатній) частині комплексної площини не є мінімально фазовими і їх характеристики можуть не відповідати характеристикам, наведеним у табл.4.

Слід зауважити, що знаменник передаточної функції системи є її характеристичним поліномом, а рівняння, в якому знаменник передаточної функції прирівнюється до нуля, - це характеристичне рівняння системи.

8. Приклад побудови логарифмічних частотних характеристик

Розглянемо приклад побудови логарифмічних частотних характеристик послідовно з’єднаних ланок.

Схема з’єднання ланок показана на рис.6.21.

Рис. 6.21 – Приклад послідовно з’єднаних ланок.

Передаточні функції ланок:

,; .

Коефіцієнт підсилення К= К₁К₂К₃ = 200.

Рівень горизонтальної асимптоти L=20lgK=46дБ.

Постійні часу ланок: Т₁= 0,9; Т₂= 0,005; Т₃= 0,05.

Частоти спряження: ; ; ;

Десяткові логарифми частот спряження: lgω₁=0,046; lgω₂=2,3; lgω₃=1,3;

Перша ланка - першого порядку, нахил асимптоти -20 дБ/дек, зсув фаз -90^0,

Друга ланка ланка - першого порядку, нахил асимптоти -20 дБ/дек, зсув фаз -90⁰

Третя ланка - другого порядку, нахил асимптоти -40 дБ/дек, зсув фаз -180⁰

Побудована АФЧХ показана на рис. 6.22

Будуємо горизонтальну асимптоту на рівні L=46 дБ.

Відкладаємо за віссю абсцис значення десяткових логарифмів частоти.

Проводимо від першої зліва частоти спряження вертикальну лінію до перетину з горизонтальною асимптотою.

Будуємо похилу асимптоту ланки, яка відповідає даній частоті спряження. У нашому випадку це асимптота з нахилом -20 дБ/дек.

З наступної частоти спряження проводимо вертикальну лінію до перетину з похилою асимптотою.

Будуємо похилу асимптоту, додаючи до кута нахилу попередньої асимптоти кут нахилу асимптоти даної ланки.

У такому ж порядку будуємо всі асимптоти.

З’єднуємо асимптоти плавною лінією, враховуючи, що для ланки першого порядку лінія проходить на 3 дБ нижче точки перетину асимптот, а для ланки другого порядку значення залежить від величини постійної затухання ланки. У нашому випадку d=0,5.

Побудована ЛАЧХ показана на рис.6.22, а.

Логарифмічну фазово-частотну характеристику будуємо в такому порядку. Відкладаємо частоти спряження.

Відповідно до порядку ланки відкладаємо границі зсуву фаз для кожної ланки. Залежно від типу ланки вибираємо ширину смуги. Для наступної ланки діапазон зсуву фаз будуємо після побудови такого діапазону для попередньої ланки. Якщо ланка диференційна, то смугу частот відкладаємо вверх.

Ділимо діапазони кожної ланки на половину і ставимо точки на частотах спряження.

Через поставлені точки проводимо фазові характеристики кожної ланки у вигляді арктангенса.

З’єднуємо характеристики окремих ланок суцільною лінією і одержуємо ЛФЧХ нашої системи.

Приклад побудови показано на рис. 6.22, б.

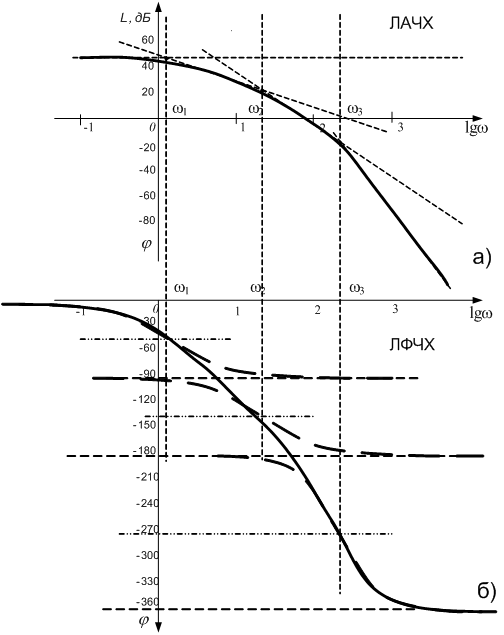
Рис.6.22 – Приклад побудови логарифмічних частотних характеристик

Для більш складної системи логарифмічні частотні характеристики можуть бути побудовані за математичним виразом передаточної функції системи, яку можна обрахувати згідно із структурною схемою системи.

Контрольні запитання для перевірки засвоєння навчального матеріалу

1. Які частотні характеристики ви знаєте?

2. Що таке децибел?

3. Який порядок побудови логарифмічних частотних характеристик динамічної ланки?

4. Яка частота називається частотою спряження?

5. Який зсув фаз коливальної ланки на частоті спряження?

6. Який максимальний зсув фаз коливальної ланки?

7. Чому дорівнює нахил асимптоти ЛАЧХ коливальної ланки?

8. Яке значення має ЛАЧХ коливальної ланки, в якої постійна затухання D=1 на частоті спряження?

9. Який вигляд має АФЧХ коливальної ланки?

10. Запишіть комплексну передатну функцію коливальної ланки.

11. Як зміниться АФЧХ коливальної ланки при зміні коефіцієнта підсилення?

12. Як зміниться АФЧХ коливальної ланки при зміні постійної часу?

13. Як зміниться АФЧХ коливальної ланки при зміні коефіцієнта демпфірування?

14. Нарисуйте вигляд ЛАЧХ реальної диференційної ланки?

15. Який нахил асимптоти реальної диференційної ланки?

16. Чому дорівнює максимальний зсув фази реальної диференційної ланки?

17. Які ланки називають мінімально фазовими?

18. Як залежить максимальний зсув фаз від порядку рівняння динамічної ланки?

19. Назвіть порядок побудови логарифмічних частотних характеристик декількох послідовно з’єднаних ланок.

20. Побудуйте ЛАЧХ та ДФЧХ двох послідовно з’єднаних ланок різних типів.

Розділ 7. Стійкість, точність та якість САК