Вопрос 54. Ряды распределения :понятия виды. Показатели вариации признака.

Составной частью сводной обработки данных статистического наблюдения является построение рядов распределения. Цель его - выявление основных свойств и закономерностей стат. совокупности.

Различают два типа рядов распределения:

атрибутивный;

вариационный.

Ряды распределения, построенные по качественным признакам, называют атрибутивными. (Например, распределение население по полу, характеру труда, национальности и т.д.)

Ряды распределения, построенные по количественному признаку называются вариационными. Числовые значения признака - вариантами.

Рассматривая первичный ряд можно видеть, что варианты признака у отдельных единиц совокупности повторяются.

Число повторений отдельных вариантов называют частотой (обозначим ѓ)

Сумма частот, равная объему изучаемой совокупности - n.

По характеру вариации различают дискретные и непрерывные признаки.

Дискретные признаки отличаются друг от друга на некоторую конечную величину, т.е. даны в виде конкретных чисел. (Например, число детей в семье).

Непрерывные признаки могут отличаться друг от друга на сколь угодно малую величину и в определенных границах принимать любые значения. Например, зарплата рабочих, % выполнения.

Способы построения вариационного ряда для этих видов признаков различны. Для построения дискретного ряда с небольшим числом вариантов достаточно перечислить все встречающиеся варианты значений признака (x_i), а затем подсчитать частоту повторений каждого варианта ѓ_{i. (}Например, распределение студентов по успеваемости и т.п.)

  Вариация - это различие в значениях какого- либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Например, работники фирмы различаются по доходам, затратам времени на работу, росту, весу, любимому занятию в свободное время и т.д. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Таким образом, величина каждого варианта объективна.

Для характеристики колеблемости признака используется ряд показателей, такие как размах вариации, определяемый как разность между наибольшим (х _мах ) и наименьшим (х _т щ) значениями вариантов:

R = X_max ^— X_min ^.

Среднее линейное отклонение исчисляют для того, чтобы дать обобщающую характеристику распределению отклонений, которое учитывает различия всех единиц изучаемой статистической совокупности. Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней без учета знака этих отклонений:

На практике меру вариации более объективно отражает показатель дисперсии ( 2 – средний квадрат отклонений), определяемый как средняя из отклонений, возведенных в квадрат (х – х₁)₂ :

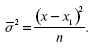
Корень квадратный из дисперсии 2 среднего квадрата отклонений представляет собой среднее квадратическое отклонение ?² и ?– общепринятые меры вариации признака.

Среднее квадратическое отклонение – это мерило надежности средней.

Свойства дисперсии (доказываемые в математической статистике), которые позволяют упростить расчеты:

1) если из всех значений вариант отнять какое–то постоянное число А² , то средний квадрат отклонений от этого не изменится;

2) если все значения вариант разделить на какое–то постоянное число А, то средний квадрат отклонений уменьшится от этого в А₂ раз, а среднее квадратическое отклонение – в А раз

3) если исчислить средний квадрат отклонений от любой величины А, которая в той или иной степени отличается от средней арифметической х, то он всегда будет больше среднего квадрата отклонений ?² , исчисленного от средней арифметической.