24.Визначення недоступних для вимірювання мірною стрічкою віддалей.

На практиці зустрічаються випадки, коли через якісь перешкоди (яр, річка, болото, будівля) не можна виміряти стрічкою відстань між точками. У цих випадках перешкоду можна обійти, відкладаючи екером чи якимсь кутомірним приладом прямі кути, або визначити відстань, використавши теорему синусів (відношення сторін трикутника дорів­нює відношенню синусів протилежних кутів).У першому випадку довжину лінії АВ визначають як суму довжин відрізків:

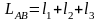
У другому випадку відстань х визначають за базисом b₁, який вимірюють стрічкою, та двома кутами a₁ і b₁, які вимірюють те­одолітом. Для контролю рекомендується виміряти й третій кут у₁. Трикут­ники мають бути такими, щоб кути навпроти базису та сторони, яку вимірюють, були в межах 30-150°. Визначення відстані контролюють за результатами вимірювання другого базису b₂ та кутів a₂ і b₂ За тео­ремою синусів знаходять:

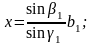
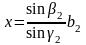
Відносна розбіжність між двома значеннями відстані не повинна перевищувати 1:1000. Якщо це так – знаходять середнє значення з двох результатів.

27. Обробка кутових вимірювань в теодолітних ходал

Обчислювальні роботи з визначення координат вершин теодолітного ходу включають в себе: 1) обробку кутових вимірів і обчислення дирекційний кутів сторін; 2) обчислення горизонтальних проекцій сторін; 3) обчислення збільшень координат і координат вершин ходу. Всі обчислення ведуться в спеціальній відомості. Обчислювальні роботи для замкнутих і розімкнутих (діагональних) ходів мають свою специфіку. Тому розглянемо кожен з цих випадків роздільно. Обробка кутових вимірів і обчислення дирекційний кутів сторін. У той же час теоретична сума кутів, визначена за відомою формулою геометрії, зобов'язана бути рівна. Різниця суми виміряних кутів і теоретичної суми кутів полігону іменується кутовий нев'язкої ходу. Величина кутовий нев'язки характеризує точність вимірювання кутів; вона не зобов'язана бути більше максимально допустимої величини. Якщо фактична кутова нев'язка не перевершує допустиму, тобто виконується умова то якість кутових вимірів слід визнати задовільним. У неприємному випадку копітко інспектують обчислення і записи в журналах та відомості і, переконавшись в їх непомильності, повторюють польові виміри всіх або окремих кутів полігону

28. Плоскі прямокутні координати.

Система плоских прямокутних координат. При розгортанні зон у площину проекція Гауса задає в кожній зоні систему прямокутних координат, де вісь Х — осьовий меридіан зони, а вісь Y — лінія екватора .

Необхідно відмітити, що система плоских прямокутних координат на топографічних картах (в проекції Гауса) дещо відрізняється від декартових координат на площині, які прийнято в математиці.

За вісь Х прийнята вертикальна лінія, за вісь Y — горизонтальна, тому що в топографії і геодезії орієнтування проводиться по півночі з відліком кутів за годинниковою стрілкою, а в математиці — від горизонтального напрямку проти ходу годинникової стрілки. Тому для збереження знаків тригонометричних функцій і користування таблицями тригонометричних величин положення осей координат, прийняте в математиці, повернуте на 90*.

Координати зони мають порядкові номери від 1 до 60, які зростають із заходу на схід. Західний меридіан першої зони збігається з меридіаном Гринвіча. Отже, координатні осі кожної зони займають чітко визначене положення на земній поверхні. Тому система плоских прямокутних координат будь-якої зони пов’язана і з системою географічних координат точок на поверхні Землі. При необхідності можна легко і просто обчислити прямокутні координати за відомими геодезичними координатами і навпаки.