Задачи по статистике

101. На каждые 11 страниц наборщик в среднем допускает 3 ошибки. Сколько ошибок следует ожидать на 1650 страницах?

102. Найдите медиану последовательности натуральных чисел от 1 до 7 включительно.

103. Найдите медиану ряда 6; 4; 7; 8; 12; 4; 6; 7; 5.

104. Найдите медиану ряда чисел 1,12, 5,17, 2, 8,11, 7, 9.

105. Найдите медиану ряда чисел 61,12, 54,104, 37,49.

106. Найдите среднее арифметическое последовательности натураль­ных чисел от 1 до 5 включительно.

107. Дан ряд чисел: 16, 15, 18, 12, 13, 20, 16, 14, 11. Найдите, на сколько мода этого ряда больше среднего.

108. На письменном экзамене по математике можно получить от 0 до 10 баллов. Десять учеников получили такие оценки: 10, 4, 5, 7, 7, 6, 9, 4, 8, 5. Определите, насколько размах этого ряда данных меньше его среднего.

109. Ученики 9-го класса получили следующие четвертные оценки по математике: 4, 5, 5, 3, 4, 4, 4, 3, 5, 4, 5,5, 5, 3, 3, 4, 4, 4, 4, 3. Определите процентную частоту оценки «5».

110. На уроке статистики ученики подсчитывали среднее значение своих четвертных оценок по математике. Для этого они составили таблицу и подсчитали среднее значение. Получилось 4,04. После урока одно число было стёрто. Восстановите его.

Варианты	3	4	5
Кратность	7	10

Решения избранных задач

25. Рассмотрим один объект. Вероятность того, что он не будет найден ни одной из m станций равна (1 — р)^т, тогда вероятность того, что он будет найден хотя бы одной станцией, равна 1 — (1 — р)^т. Вероятность того, что каждый объект будет обнаружен хотя бы одной станцией, равна (1 - (1 -р)^т)^к. Значит, искомая вероятность равна 1 - (1 - (1 -р)^т)^к.

Ответ: 1 - (1 - (1 -р)^т)^к.

30. Фраза «прибор окончательно выйдет из строя в точности при k-м испытании» означает, что прибор выйдет из строя после одного из 1, 2,... ,(k — 1)-го испытаний и при k-м испытании.

Вероятность того, что прибор выйдет из строя при первом и k-м ис­пытаниях, равна р• (1 — р)… (1 – р) • р = р² • (1 — р)^к-2, при втором и k-м — (1 - р) • р • (1 - р)... (1 - р) •р = р² • (1 - р)^к-2, и так далее.

Вероятность того, что прибор выйдет из строя при (k — 1)-м и k-м испытаниях, равна (1 — р)... (1 — р) •р• р = (1 — р)^к-2• р².

Искомая вероятность равна р² • (1 - р)^к-2 +…+ р² • (1 — р)^к-2 = (к-1) •р²• (1-р)^к-2.

Ответ: (k - 1) • р²• (1 - р)^к-2.

31. Предположим, имеется п запасных устройств, тогда вероятность правильной работы равна 1—р^п+1. Искомые значения п находятся из неравенства 1 -pⁿ⁺¹ р; pⁿ⁺¹ 1- р; n +1 log_p (1 -р);п log_p(l -р) - 1.

Ответ: п log_p(l -р) - 1.

44. В данном примере эксперимент состоит в том, что случайным об­разом отмечаются 6чисел из 36 в карточке «Спортлото». Поэтому равновозможными элементарными событиями будут наборы из шести от­меченных чисел. Так как для определения того, произойдёт или не про­изойдёт событие А (среди отмеченных чисел — k чисел выигрышные), порядок чисел не существенен, то в качестве равновозможных элемен­тарных событий достаточно рассматривать неупорядоченные наборы 6 чисел из 36. Следовательно, число равновозможных элементарных со­бытий равно С⁶₃₆. Событие А состоит из наборов 6 чисел, k из которых выигрышные, а 6 - к — проигрышные. Набор из к выигрышных чисел можно выбрать С$ способами, а набор 6 - к проигрышных чисел можно выбрать С^6-к₃₀ способами. Тогда по основному принципу комбинатори­ки набор из k выигрышных и 6 - k проигрышных чисел можно выбрать С^к₆С^6-к₃₀

способами, следовательно, Р(А) = .

Для k = 6 получаем Р(А) = =

Ответ:

45. Всего существует С⁴₆ = 15 вариантов удалить 4 файла из 6. Из нихС²₂•С²₄= 6 вариантов, при которых оба вирусных файла будут удалены.

Искомая вероятность равна 0,4.

Ответ: 0,4.

46. Вероятность того, что первый раз выпала не карта червонной масти, равна , аналогично для второго раза.

47. Значит, искомая вероятность равна ² = = 0,5625.

Ответ: 0,5625.

48. Вероятность того, что решка выпадет ровно 3 раза, равна 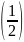³ = .

1 3

Вероятность того, что решка выпадет ровно 2 раза, равна С²₃ • = .

13 1

Искомая вероятность равна + = .

Ответ: 0,5.

49. При п бросках вероятность того, что решка не выпала ни разу, равна ⁿ . Так как ² при п 7, то минимальное число равно 7.

Ответ: 7.

50. Вероятность вытащить белый кубик равна = . Вероятность получить чётное число очков на уже заданном кубике равна . Искомая вероятность равна = 0,2.

Ответ: 0,2.

51. Чисел, которые делятся на 3, среди не превышающих 200—66. Чисел, которые делятся на 6, — 33. Значит, тех, которые делятся на 3, но не делятся на 2, 66 — 33 = 33. Следовательно, искомая вероятность = 0,165.

Ответ: 0,165.

52. Вероятность того, что 2 чёрные ручки окажутся у II школьника, равна = ( - вероятность того, что I школьник станет обменивать чёрную ручку, — II станет обменивать ручку другого цвета). Так как по условию школьники не пронумерованы, то искомая вероятность = 0,375.

Ответ: 0,375.

53. Вероятность того, что оба раза выпадет не карта червонной масти, равна ², значит, искомая вероятность равна 1 - = = 0,4375.

Ответ: 0,4375.

61. На место водителя можно посадить только одного из двух человек (умеющего водить машину), значит, существуют 2 способа занять первое место. Второе место может занять любой из 5 человек, оставшихся после того, как место водителя будет занято. Третье место — 4 человека и т. д. Получаем произведение:

2• 5• 4• 3• 2• 1 = 240.

Ответ: 240.

67. На первом месте всегда должна стоять одна буква, следовательно, существует только один способ занять первое место. На оставшиеся два места может претендовать любая из 10-ти букв, так как буквы в позыв­ных могут повторяться. Получаем 1 • 10 • 10 = 100.

Ответ: 100.

65. На первом месте может стоять любая из 26 букв. На остальных ме­стах — любые из девяти цифр, причём они могут повторяться. Получаем 26 • 9 • 9 • 9 = 18954.

Ответ: 18954.

65. На завтрак людоед может предпочесть любого из 10 человек, тогда на обед — любого из 9 оставшихся, а на ужин — одного из 8 оставшихся пленников. Всего получаем 10 • 9 • 8 = 720 способов.

Ответ: 720.

88. Сначала поставим на любую из 64 клеток доски белую ладью. Для чёрной ладьи останется 49 полей. Всего получаем 64 • 49 = 3136 спосо­бов.

Ответ: 3136.