
- •Тема 3.1. Элементы комбинаторики и теории вероятностей. № 22. Основные понятия комбинаторики. Вероятность события. (2 часа – лекция)
- •Тема 3.2. Элементы математической статистики.
- •Демонстрационный вариант
- •Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Вариант № 6
- •Вариант № 7
- •Вариант № 8
- •§ 2. Сборник задач Задачи по теории вероятностей
- •Задачи по комбинаторике
- •Задачи по статистике
- •Решения избранных задач
- •Ответы к тренировочным тестам
- •Ответы к сборнику задач
- •Литература
Тема 3.1. Элементы комбинаторики и теории вероятностей. № 22. Основные понятия комбинаторики. Вероятность события. (2 часа – лекция)
Изучение нового материала:
Элементы комбинаторики.
Под комбинаторикой понимается раздел математики, изучающий комбинации и расстановки n по m элементов . Формулы комбинаторики широко применяются в теории вероятностей.
Группы, составленные из каких – либо элементов, называются соединениями.
Различают три основных вида соединений: размещения, перестановки и сочетания.
Задачи, в которых производится подсчет возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными. Раздел математики, занимающийся их решением, называется комбинаторикой.
Размещения. Размещениями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их расположения.
Итак, под размещением n по m элементов ( m всегда <= n ) понимаются различные комбинации объектов между собой с учетом порядка. Например, из 2х элементов A и B можно составить всего 2 комбинации: AB и BA . А вот 3 элемента A, B и С уже можно разместить следующими способами (если за m принять 2 любых элемента): AB, AC, BC, BA, CA, CB, всего 6 способов.
Число
размещений из n
элементов по m
обозначается
 и вычисляется по формуле:
= n(n
– 1)(n
– 2)
и вычисляется по формуле:
= n(n
– 1)(n
– 2) .
.
2.Перестановки. Перестановками из n элементов называются такие соединения из всех n элементов, которые отличаются друг от друга порядком расположения элементов.
Число
перестановок из n
элементов обозначается
 :
:
=
 = n(n
– 1)(n
– 2)
= n(n
– 1)(n
– 2) или
= 1
или
= 1 n.
n.
Произведение 1 n обозначают n! ( n –факториал), причем 0! = 1, 1! = 1.
Следовательно:
= n!
=
 =
=

При решении задач часто используют равенство:
 =
(n
– m)
.
=
(n
– m)
.
3.Сочетания. Сочетаниями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.
Т.е.разница между размещением и сочетанием заключается лишь в том, что в последнем не учитывается порядок элементов.
Число
сочетаний из n
элементов по m
обозначается
 .
Оно находится по формуле :
.
Оно находится по формуле :
=
 ,
которую можно записать также в виде
=
,
которую можно записать также в виде
=
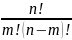 или
или
=
 .
.
При
решении задач используют и другие
формулы:
=
 (0
(0
 =
1,
=
1,
 = 1,
= 1,
 =
=
 .
.
Вероятность события.
Изучение каждого явления в порядке наблюдения или производства опыта связано с осуществлением некоторого комплекса испытаний. Всякий результат или исход испытания называется событием.
Если событие при заданных условиях может произойти или не произойти, то оно называется случайным.
В том случае, когда событие должно непременно произойти, его называют достоверным, а в том случае, когда оно заведомо не может произойти, - невозможным.
Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий.
События называются несовместными, если каждый раз возможно появление только одного из них.
События называются совместными, если в данных условиях появление одного из этих событий не исключает появление другого при том же испытании.
Классическим примером несовместных событий является результат подбрасывания монеты – выпадение лицевой стороны монеты исключает выпадение обратной стороны (в одном и том же опыте).
События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны.
Полной группой событий называется совокупность всех возможных результатов опыта.
События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.
В приведенном выше примере появление красного и зеленого шаров – равновозможные события, если в коробке находится одинаковое количество красных и зеленых шаров.
Если же в коробке красных шаров больше, чем зеленых, то появление зеленого шара – событие менее вероятное, чем появление красного.
Исходя из этих общих понятий можно дать определение вероятности.
Классическое определение вероятности.
Вероятностью события А называется отношение числа исходов m, благоприятствующих наступлению данного события А, к числу n всех исходов (несовместных, единственно возможных и равновозможных), т.е.
Р (А) =
(А) =

Вероятность
любого события не может быть меньше
нуля и больше единицы, т.е. 0
 Невозможному событию соответствует
вероятность Р(А) = 0, а достоверному –
вероятность Р(А) = 1.
Невозможному событию соответствует
вероятность Р(А) = 0, а достоверному –
вероятность Р(А) = 1.
Пример. В коробке находится 10 шаров. 3 из них красные, 2 – зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет красным, зеленым или белым.
Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С.
Тогда в соответствием с записанными выше формулами получаем:
Р(А)
=
 = 0,3.
= 0,3.
Р(В)
=
 = 0,2.
= 0,2.
Р(С)
=
 = 0,5.
= 0,5.
Решить задачи:
Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа без повторений цифр. Выяснить, сколько среди этих пятизначных чисел таких, которые не начинаются с 543.
На выпускном вечере 20 выпускников техникума обменялись фотокарточками. Сколько при этом было роздано фотокарточек?
Из 20 рабочих нужно выделить шестерых для работы на стройучастке. Сколькими способами можно это сделать?
Из слова «автоматика» выбирается наугад одна буква. Какова вероятность того, что это буква «а»?
Решение:
 =
5! = 1
=
5! = 1 2
3
4
5
= 120 – всевозможные перестановки из
пяти цифр,
2
3
4
5
= 120 – всевозможные перестановки из
пяти цифр,
 =
2! = 1
=
2! = 1 = 2 - всевозможные перестановки из двух
цифр (1 и 2), т.е. пятизначных чисел,
начинающихся на 543 всего – 2.
= 2 - всевозможные перестановки из двух
цифр (1 и 2), т.е. пятизначных чисел,
начинающихся на 543 всего – 2.
Р
= 120
 2 = 118 - пятизначных чисел таких, которые
не начинаются с 543.
2 = 118 - пятизначных чисел таких, которые
не начинаются с 543.
 =
20
=
20
 = 20
= 20
 = 380.
= 380. =
=
 =
=
 =
=
 = 38760.
= 38760.Событие А – выбранная буква «а», m = 3, n = 10.
Р(А) = = 0,3.
Теоремы вероятностей.
Т.сложеня вероятностей несовместных событий.
Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р(А + В) = Р(А) + Р(В).
Т.сложеня вероятностей совместных событий
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р(А + В) = Р(А) + Р(В) Р(АВ).
Событие,
противоположное событию А (т.е.
ненаступление события А), обозначают
 .
Сумма вероятностей двух противоположных
событий равна единице:
.
Сумма вероятностей двух противоположных
событий равна единице:
Р(А)
+ Р( = 1.
= 1.
Вероятность
наступления события А , вычисленная в
предположении, что событие В уже
произошло, называется условной
вероятностью
события А при условии В и обозначается
 .
.
Если
А и В – независимые события, то Р(В)

 .
.
События А, В, С, … называются независимыми в совокупности, если вероятность каждого из них не меняется в связи с наступлением или ненаступлением других событий по отдельности или в любой их комбинации.
Т.умножения вероятностей независимых событий.
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
Р(АВ)
= Р(А)

Т.умножения вероятностей зависимых событий.
Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность другого:
Р(АВ)
= Р(А)
 = Р(В)
= Р(В)
 .
.
Формула полной вероятности.
Пусть
события
 образуют полную группу событий и при
наступлении каждого из них, например
образуют полную группу событий и при
наступлении каждого из них, например событие
А может наступить с некоторой условной
вероятностью
событие
А может наступить с некоторой условной
вероятностью .
тогда вероятность наступления события
А равна:
.
тогда вероятность наступления события
А равна:
Р(А)
= Р( + Р(
+ Р( + … + Р(
+ … + Р(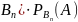 ,
где
,
где
Р( Р(
Р( + … +Р(
+ … +Р( = 1.
= 1.
Пусть
событие А может наступить лишь при
условии появления одного из несовместных
событий
,
которые образуют полную группу событий.
Если событие А уже произошло, то
вероятности событий могут быть переоценены
по формуле
Байеса:
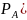 )
=
)
=
 .
.
Задание: Н.В.Богомолов, стр.259, № 7,8, 9,10, 12(1), 13, 14, 19, 21, 23, 28(1).
Дома: Н.В.Богомолов, стр. 259, № 16, 20, 24(1), 26.
стр. 262, № 33,35.
Проверить решение:
№ 7. Найдите число размещений:
 =
=
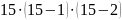 = 15
= 15 = 2730.
= 2730. =
=
 =
=
 5.
5.
№ 8. Вычислите:
 ;
;
 =
7
=
7 =210,
=210,
 = 6
= 6 = 120,
= 120,
 = 5
= 5 = 60,
= 60,
= 210 + 120 + 60 = 390.
 ;
;
 =
6
=
6 = 720
= 720
 =
6
=
6 = 360
= 360
= 6 = 120
=
 =
=
 =
=
 = 9.
= 9.
№23 - 24.Практические занятия. Решение задач на нахождение вероятностей событий
Повторение: Испытанием называется любой опыт, наблюдение, эксперимент и т.д. (Пример: бросание монеты) . Событием называется результат этого испытания (Пример: орел или решка в испытании с бросанием монеты). Совместимыми событиями называются такие события, что одно из событий не исключает появление другого (Пример: два раза бросил монету и 2 раза выпал орел). Несовместимыми событиями называются такие события, в которых, появление одного из них в одном испытании исключает появление другого (Пример: один раз бросили монетку, может выпасть либо орел, либо решка, и не может выпасть и того и другого одновременно). Попарной несовместимостью называется несовместимость более чем 2-х событий (Пример: бросили один раз игральную кость, выпала единица, все остальные грани попарно несовместимы). Противоположными событиями называются такие события, которые несовместимы, и в то же время происходит одно их них (Пример: бросили монетку, выпал орел, выпадение решки противоположное событие). Достоверным событием называется такое, которое является единственно возможным исходом испытания (Пример: купили часы китайского производства, а они взяли да и сломались, потому что просто не могли не сломаться :) ).
Стр.262, №33. Н.В.Богомолов, «Практические занятия по математике».
Решение:
I – 300 д.
– 300 д.
II – 200д. 550д.
III – 50д.
А – вынутый шар I сорта.
В - вынутый шар II сорта.
C - вынутый шар III сорта.
Р(А)
=
=
 = 0,545.
= 0,545.
Р(В)
=
=
 = 0,364.
= 0,364.
Р(С)
=
=
 = 0,09.
= 0,09.
№2. В группе 25 студентов. Из них отлично успевают по математике 5 человек, хорошо – 12, удовлетворительно – 6. Преподаватель, не знакомый с группой, вызывает по списку одного студента. Найти вероятность того, что вызванный студент будет успевающий.
Решение:
n = 25,
m = 23
А – вызванный студент – успевающий.
Р(А)
=
 = 0,92.
= 0,92.
№34.
Решение:
Было стало
Б – 20 19 34
– 20 19 34
Ч – 15 15
А – вынутый шар – белый.
Р(А)
=
 = 0,559.
= 0,559.
№35.
Решение:
Б – 7 12
– 7 12
Ч – 5
А – выбранный шар – черный.
1)Р(А)
=
 = 0,42.
= 0,42.
2)В – два наудачу выбранных шара – черные.
n
=
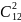 =
=
 =
=
 =
=
 = 66,
= 66,
m
=
 =
=
 =
=
 =
=
 = 10,
= 10,
Р(В)
=
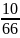 = 0,15.
= 0,15.
стр. 263, № 40.
Решение:
10 –деталей,
4 – стандартных,
3 – взяли.
А – хотя бы 1 деталь стандартная,
В -1 деталь стандартная, 2 нестандартные,
С - 2 детали стандартные, 1 нестандартная,
D -3 детали стандартные,
А = В + С + D, ⟹ Р(А) = Р(В) + Р(С) + Р(D).
Р(В)
=
 =
=
 =
=
 = 0,5.
= 0,5.
Р(С)
=
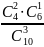 =
=
 =
=
 =
=
 = 0,3.
= 0,3.
Р(D)
=
 =
=
 =
=
 = 0,03.
= 0,03.
Р(А) = 0,5 + 0,3 + 0,03 = 0,83.
2 – ой способ:
А – хотя бы 1 деталь стандартная,
- ни одна из взятых деталей не является стандартной.
Р(А) + Р( ) = 1.
Р(
)
=
 =
=
 =
=
 =
=
 = 0,17.
= 0,17.
Р(А) = 1 0,17 = 0,83.
Стр. 264, № 46.
Решение:
n = 6,
m = 3
А – первый шар – белый.
В – второй шар – белый.
Р(А)
=
 = 0,5.
= 0,5.
 =
5,
=
5,
 =
2
=
2
Р(В)
= =
 = 0,4
= 0,4
Р(АВ)
= 0,5 = 0,2.
= 0,2.
№ 3.
В ящике имеется 20 деталей, из которых три – нестандартные. Из ящика берутся наугад в результате двукратного испытания две детали. Найти вероятность того, что детали окажутся нестандартными.
Решение:
n = 20,
m = 3.
А – первая выбранная деталь – нестандартная,
В – вторая выбранная деталь – нестандартная.
Р(А)
=
 = 0,15.
= 0,15.
= 19,
= 2.
РА(В)
=
 = 0,105.
= 0,105.
Р(АВ) = Р(А) РА(В) = 0,15 0,105 = 0,016.
Стр.267, № 55.
n = 4, k = 3, p = 0,8, q = 0,2.
По
формуле Бернулли:
(k)
=
 ,
где q
= 1 – p.
,
где q
= 1 – p.
 (3)
=
(3)
=
 =
=
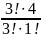
 = 4
= 4 = 0,41.
= 0,41.
стр.264, № 57.
№ 60.
 =
=
 , n
- ?
, n
- ?
 =
=
 =
=
 =
=
90 = 5
= 5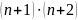
90n
270 = 5( +
2n + n + 2)
+
2n + n + 2)
90n 270 = 5 + 10n + 5n + 10
5 + 15n + 10 90n + 270 = 0
5 75n + 280 =0
75n + 280 =0
15n + 56 = 0
D = 225 224 = 1,
=
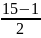 = 7,
= 7,
 =
=
 = 8.
= 8.
№61.
Б – 6 шаров,
– 6 шаров,
Ч – 10 шаров. 16 шаров.
А –два вынутых шара – черные.
Р(А)
=
 =
=
 =
=
 =
=
 =
=
 =
=
 = 0,375.
= 0,375.
2 – ой способ:
А- первый выбранный шар будет черный,
В - второй выбранный шар будет черный
n = 16, m = 10
Р(А)
=
 = 0,625,
= 0,625,
= 15, = 9.
РА(В)
=
 = 0,6.
= 0,6.
Р(АВ) = 0,625 0,6 = 0,375.
№62.
Б – 6 шаров,
Ч – 4 шара. 10 шаров
А – первый вынутый шар – черный,
В – второй вынутый шар – черный.
n = 10, m = 4.
Р(А)
=
 = 0,4.
= 0,4.
= 9, = 3.
РА
(В)
=
 = 0,333.
= 0,333.
Р(АВ)
= Р(А)
РА
(В)
= 0,4
 = 0,133.
= 0,133.
№63.
Б –15 шаров,
Ч – 6 шаров. 21 шар.
А – первый вынутый шар – белый,
В – повторно вынутый шар – белый.
Р(А)
=
 = 0,714.
= 0,714.
Р(В) = = 0,714
Р(АВ) = 0,714 0,714 = 0,51.
№64.
2
Б –10 шаров, Б – 4шара,
Ч – 2 шара. 12 шаров. Ч – 8 шаров. 12 шаров.
А – вынутый шар из первой урны – черный,
В - вынутый шар из второй урны – черный,
Р(А)
=
 = 0,166.
= 0,166.
Р(В)
=
 = 0,667.
= 0,667.
Р(АВ) = 0,11.
№65.
В – первая взятая буква «ч»,
С – вторая взятая буква «и»,
D – третья взятая буква «с»,
Е – четвертая взятая буква «л».
Р(В)
=
 , Р(С) =
, Р(С) =
 , Р(D)
=
, Р(D)
=
 , Р(Е) =
, Р(Е) =

Р(ВСDE)
=

 = 0,0083.
= 0,0083.
№66.
А – первый стрелок попадет в цель,
В - второй стрелок попадет в цель,
С - третий стрелок попадет в цель,
Р(А)
=
 , Р(В) =
, Р(В) =
 , Р(С) =
, Р(С) =
 .
.
Р(АВС)
=
 = 0,54.
= 0,54.
№67.
№68.
1 линия – 50% всех деталей, 0,025 – нестандартных,
2 линия – 30% всех деталей, 0,02 – нестандартных,
3 линия – 20% всех деталей, 0,015 – нестандартных.
 -
деталь изготовлена на 1 –ой линии,
-
деталь изготовлена на 1 –ой линии,
 -
деталь изготовлена на 1 –ой линии,
-
деталь изготовлена на 1 –ой линии,
 -
деталь изготовлена на 1 –ой линии,
-
деталь изготовлена на 1 –ой линии,
А – выбранная деталь – стандартная.
Р(
)
= 0,5 , Р(
)
= 0,3, Р(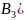 =
0,2.
=
0,2.
 (А)
= 0,975,
(А)
= 0,975,
 (А)
= 0,98,
(А)
= 0,98,
 (А)
= 0,985, т.к. Р(А)
+ Р(
)
= 1.
(А)
= 0,985, т.к. Р(А)
+ Р(
)
= 1.
Р(А)
= Р(
) (А)
+ Р(
)
(А)
+ Р(
) (А)
+ Р(
(А)
+ Р( (А)
= 0,5
0,975
+ 0,3
0,98
+ 0,2
0,985 = 0,979.
(А)
= 0,5
0,975
+ 0,3
0,98
+ 0,2
0,985 = 0,979.
№69.
№70.
С –60 деталей,
Н – 40 деталей. 100 деталей.
А – первая взятая наудачу – стандартная деталь,
В – вторая взятая наудачу – нестандартная деталь.
n = 100, m = 40.
Р(А)
=
 = 0,4
= 0,4
= 100, = 60.
РА(В)
=
 = 0,60
= 0,60
Р(АВ) = Р(А) РА(В) = 0,4 0,60 = 0,24.
Зачетная работа по теме « Элементы комбинаторики и теории вероятностей».
Н.В.Богомолов, «Практические занятия по математике». Стр.268, В – 1,2.
Вариант – 1.
