4.1 Просмотр результатов

Чтение результатов

1. Просматриваем деформированную и недеформированную формы:

General Postproc> Plot Results> Deformed Shape

2. Выводим на экран анимацию деформированной формы

PlotCtrl>Animate>Deformed Shape

Задаем параметры отображения

3. Строим распределение эквивалентных напряжений по теории Хубера-Мизеса:

General Postproc> Plot Results> Contour plot> Element solution> stress> Von Mises stress.

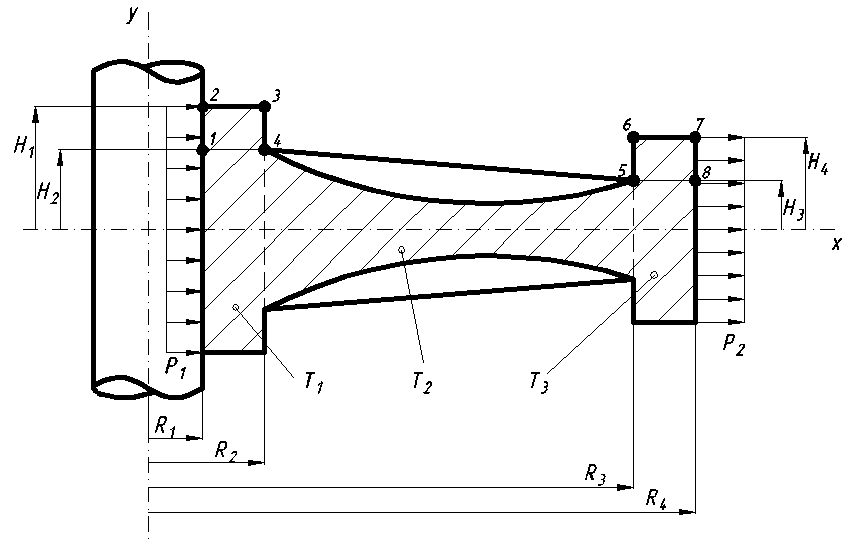
Геометрия

R1 = 25 мм

R2 = 66 мм

R3 = 250 мм

R4 = 270 мм

H1 = 100 мм

H2 = 80 мм

H3 = 40 мм

H4 = 60 мм

Силы

Р1 = 5·10⁷ Па

Р2 = 6·10⁷ Па

Температура

Т1 = 300 ºС

Т2 = 400 ºС

Т3 = 500 ºС

Угловая скорость

 = 3000 об/мин

Коэффициент температурного расширения

α = 12·10^-5 1/с

Плотность

Ro = 7800 кг/м³

Модуль упругости

E = 2 ·10¹¹ Па

Коэффициент Пуассона

Mu = 0,25

Картинка

Описание действий

Текст программы

На данном этапе выбираем тип анализа. Требуемый тип “Structural”.

10. Двойной клик по пиктограмме «Preferences»

11. Тип анализа “Structural”

12. OK

KEYW,PR_SET,1

KEYW,PR_STRUC,1

KEYW,PR_THERM,0

KEYW,PR_FLUID,0

KEYW,PR_ELMAG,0

KEYW,MAGNOD,0

KEYW,MAGEDG,0

KEYW,MAGHFE,0

KEYW,MAGELC,0

KEYW,PR_MULTI,0

KEYW,PR_CFD,0

Задаем в параметрической форме значения требуемых величин из условия задачи:

H1 = 0.100 м R1=0.025 м

H2 = 0.080 м R2=0.066 м

H3 = 0.040 м R3=0.250 м

H4 = 0.060 м R4=0.270 м

T1=300⁰C T2=400⁰C T3=500⁰C

E = 2.e11 Па

MU = 0.25

R0=7800 кг/м³ Omega=3000 об/мин

Alfa=1.2e-5 1/c

19. Parameters >Scalar parameters>

20. Задать значение переменной.

21. Accept.

22. Задать значение следующей переменной.

23. ...

24. Close.

/PREP7

*SET,H1,0.1

*SET,H2,0.08

*SET,H3,0.04

*SET,H4,0.06

*SET,R1,0.025

*SET,R2,0.066

*SET,R3,0.250

*SET,R4,0.27

*SET,E,2e11

*SET,MU,0.25

*SET,T1,300

*SET,T2,400

*SET,T3,500

*SET,Ro,7800

*SET,Alfa,1.2e-5

*SET,Omega,3000