Задача 2 ряды динамики

При выполнении этой задачи необходимо понимать, что все показатели анализа ряда динамики в целях экономического анализа надо представлять в виде таблицы 7.

Таблица 7 - Показатели динамики

(1,стр. 155-176).

Наименование показателя	Месяцы (даты)
	1	2	3		N
Основной показатель (уровень)
Средний уровень показателя
Абсолютный базисный прирост
Абсолютный цепной прирост
1 % абсолютного прироста
Среднее значение абсолютного прироста за весь интервал исследования
Темп роста базисный
Темп роста цепной
Средний темп роста
Темп прироста базисный
Темп прироста цепной
Средний темп роста

Задачи 4,5,6 индексы

Для выполнения этих задач изучите тему «Индексы». Обратите внимание на то, что одной из задач индексного метода является соизмерение во времени двух совокупностей, состоящих из элементов, неподдающихся непосредственно суммированию. Эту задачу выполняют агрегатные индексы качественных и количественных показателей.

К агрегатным индексам качественных показателей относятся:

Индекс цен

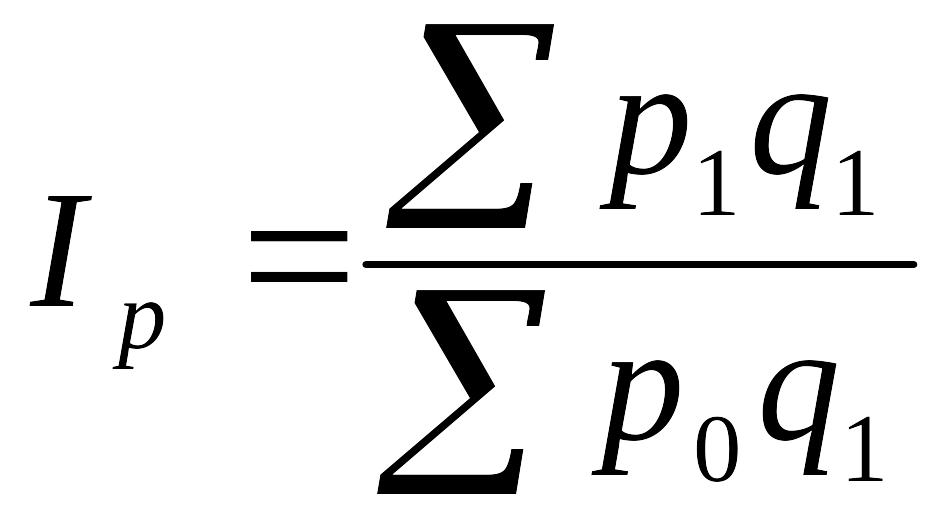
Где р - цена на товар;

q – количество проданного товара;

pq – товарооборот.

Индекс себестоимости

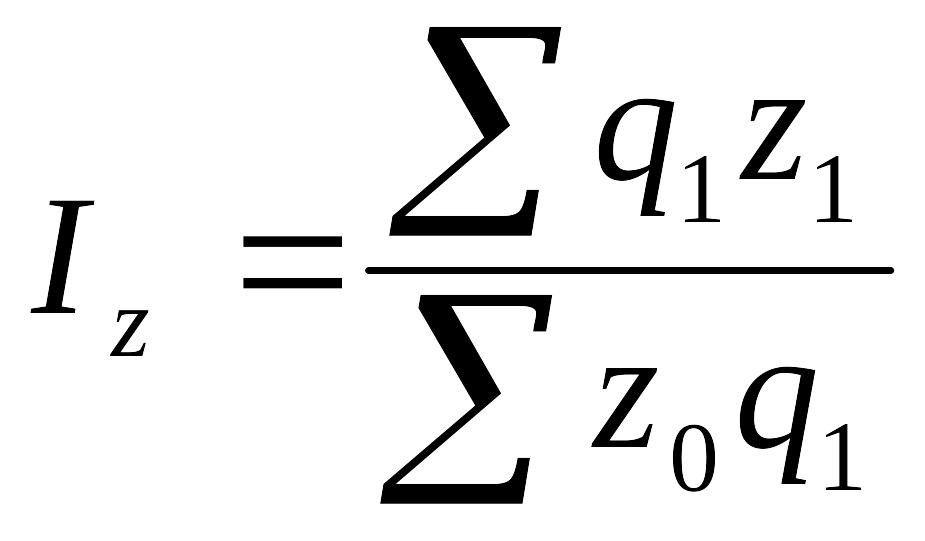
где z - себестоимость единицы продукции;

q- количество продукции;

zq - затраты на производство продукции.

К индексам количественных показателей относятся:

Индекс физического объема товарооборота

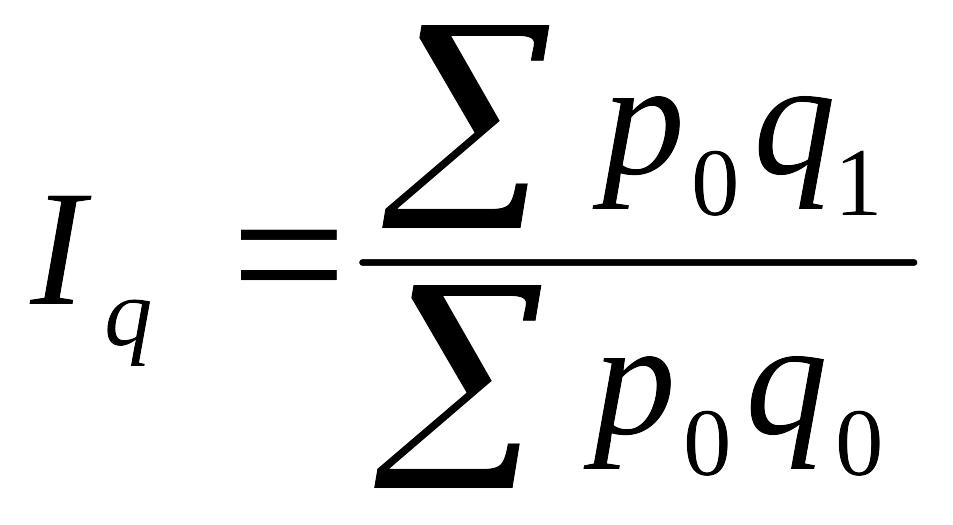
Индекс физического объема продукции

[1, стр. 206-232].

Вторая задача индексного метода – выявление влияния отдельных факторов на изменение сложного экономического явления. Для этой цели строятся системы взаимосвязанных индексов:

где - индекс затрат на продукцию:

где - индекс товарооборота, и др.

Система взаимосвязанных индексов строится с целью выявления отдельных факторов: себестоимости единицы продукции и количества произведенной продукции на изменение затрат на продукцию.

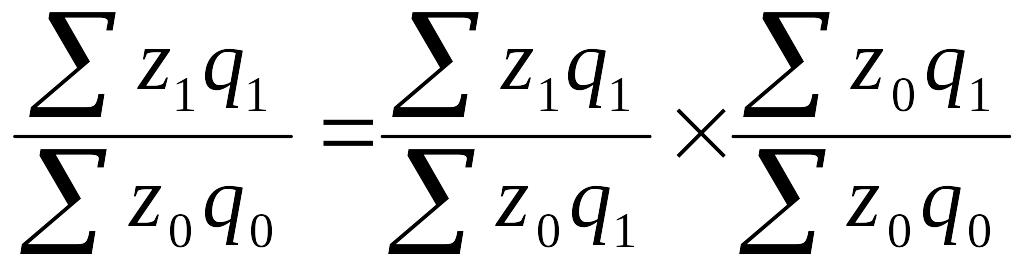
Разность между числителем и знаменателем индекса затрат - - показывает изменение затрат на продукцию за счет изменения себестоимости произведенной продукции и количества произведенной продукции.

Разность между числителем и знаменателем индекса себестоимости - отражает изменение затрат на продукцию за счет изменения себестоимости продукции.

Разность между числителем и знаменателем индекса физического объема продукции - показывает изменение затрат на продукцию за счет количества произведенной продукции.

Система взаимосвязанных индексов строится с целью выявления влияния отдельных факторов (компонентов) цены и количества на изменение товарооборота. Рассмотрим расчет индексов на примерах.

1 Себестоимость и объем продукции завода характеризуется следующими данными (см. табл. 8).

Таблица 8 – Исходные данные по изделиям

Изделия	Себестоимость единицы продукции, руб.		Выработано продукции, тыс. ед.
	Базисный период ( )	Отчетный период ( )	Базисный период ( )	Отчетный период ( )
А Б	12,0 8,0	10,0 7,4	1,0 6,4	1,1 7,2

На основании приведенных данных вычислите:

а) общий индекс затрат на всю продукцию,

б) агрегатный индекс себестоимости,

в) агрегатный индекс физического объема продукции

Определите изменение затрат на производство продукции за счет изменения количества выпускаемой продукции и себестоимости. Поясните экономический смысл исчисленных индексов.

Решение

Для вычисления индексов строим расчетную таблицу (см. табл.9)

Таблица 9 – Промежуточные расчеты

Изделия
А. шт Б. кг.	12,0 8,0	10,0 7,4	1,0 6,4	1,1 7,2	12,0 51,2	12,54 53,28	13,20 57,60
Итого	---	---	---	---	63,2	65,82	70,80

О бщий индекс затрат на продукцию определяется по формуле:

Затраты на продукцию в отчетном периоде по сравнению с базисным возросли в среднем на 4% или 2,62 тыс. руб.

Агрегатный индекс себестоимости определяется по формуле

Себестоимость продукции (изделий А и Б) в отчетном периоде по сравнению в базисным снизилась в среднем на 7,1%. Вследствие этого затраты на производство продукции снизились на 4,98 тыс. руб. или можно сказать, что предприятие получило экономию от снижения себестоимости 4,98 тыс. руб.

Агрегатный индекс физического объема продукции определяется по формуле:

Количество произведении в отчетном периоде по сравнению с базисным увеличилось в среднем на 12%. Вследствие этого затраты на производство продукции увеличились на 7,6 тыс. руб.

2,61 тыс. руб.=(-4,98 тыс.руб)+7,6 тыс.руб.

Однако для построения агрегатных индексов не всегда есть данные. Поэтому, если имеются данные об индивидуальных индексах, то в этом случае вместо агрегатных индексов используются средние индексы.

Для построения индексов качественных показателей применяется средний гармонический индекс цен:

.

Индекс себестоимости:

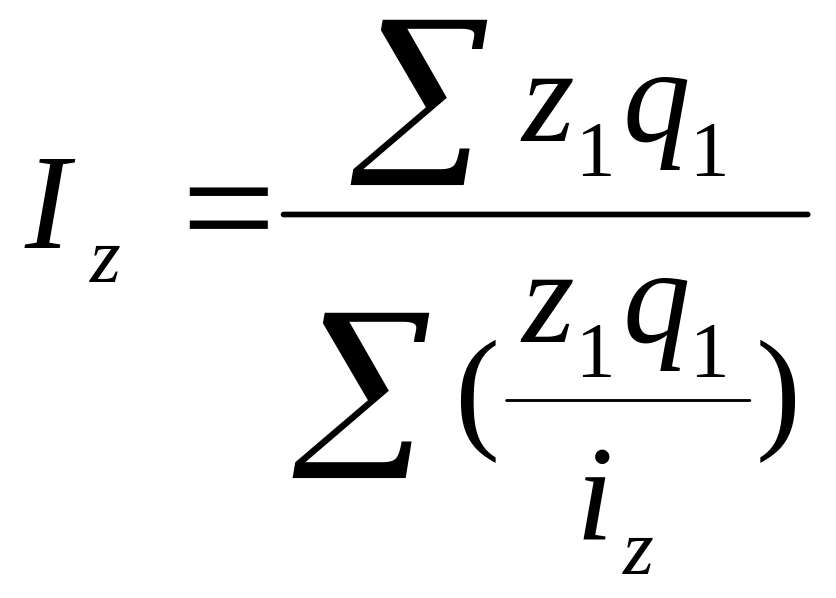
Для количественных показателей строится средний арифметический индекс физического объема товарооборота

2 Имеются следующие данные (см. табл. 10)

Таблица 10 - Данные по факторам товарооборота за два квартала

Товары	Товарооборот, тыс. руб.		Изменение цен в III кв. по сравнению со II кв.
	II кв.	III кв.
А Б	100 410	50 500	-10 +2

Вычислите средний гармонический индекс цен.

Решение:

Средний гармонический индекс цен определяется по формуле:

Цены в отчетном периоде по сравнению с базисным снизились в среднем на 2%.

3 Имеются следующие данные (см. табл. 11):

Таблица 11 - Данные по факторам объема продукции за два периода

Отрасли производства	Стоимость продукции, (млн. руб.)		Индивидуальный индекс физического объема продукции
	Базисный год	Отчетный год
А Б	25,0 30,0	30,0 38,0	1,2 1,1

Определите средний арифметический индекс физического объема продукции.

Решение

Средний арифметический индекс физ. Объема определяется по формуле: .

Физический объем продукции в отчетном периоде по сравнению с базисным увеличился в среднем на 14%.

Третьей задачей индексного метода является изучение влияния отдельных факторов на изменение средних показателей во времени. Эта задача решается путем построения системы взаимосвязанных индексов:

- индекс переменного состава,

- индекс постоянного состава,

- индекс структурных сдвигов,

По этой схеме строятся все индексы качественных показателей, например индекс себестоимости, индекс цен, индекс трудоемкости и т.д.

Построим систему взаимосвязанных индексов для изучения влияния отдельных факторов на изменение средней себестоимости:

- индекс себестоимости переменного состава.

Этот индекс показывает изменение средней себестоимости за счет двух факторов: изменения уровня себестоимости единиц продукции на отдельных предприятиях и изменения удельных весов выпуска продукции предприятиями с разным уровнем себестоимости в общем выпуске продукции, т.е. за счет структурных сдвигов.

Снижение средней себестоимости единицы продукции, например в отрасли, происходит двумя путями: в результате снижения себестоимости единицы продукции на отдельных предприятиях и за счет увеличения доли выпуска продукции там, где продукция производится с более низкой себестоимостью.

- индекс себестоимости постоянного состава показывает изменение средней себестоимости за счет изменения себестоимости на отдельных заводах.

- индекс структурных сдвигов показывает изменение средней себестоимости за счет структурных сдвигов.

Рассмотрим расчет на примере.

Имеются следующие данные по двум заводам о выпуске продукции и ее себестоимости (см. табл. 12).

Таблица 12 - Данные по двум заводам о себестоимости продукции по двум периодам

№ завода	Базисный период		Отчетный период
	Произведено единиц, шт.	Себестоимость денницы, руб.	Произведено единиц, шт.	Себестоимость единицы, руб.
1 2	400 600	10 13	850 650	9 11

Решение:

Для расчета строим расчетные таблицы 13 и 14:

Таблица 13 - Промежуточные расчеты средней себестоимости

№ завода
1 2 3	400 600 1000	10 13 ---	850 650 1500	9 11 ---	0,9 0,85 ---	4000 7800 11800	7650 7150 14800	8500 8450 16950

Таблица 14 - Сводные показатели общей себестоимости продукции

№ завода	Структура, %
1 2 3	40 60 100	57 43 100	400 780 1180	513 473 986	570 559 1129

или

Если вычислена структура (см. табл. 15) то индексы себестоимости можно определить также по формулам:

- индекс себестоимости переменного состава.

- индекс себестоимости постоянного состава.

- индекс структурных сдвигов.

Рассчитаем по вышеприведенным формулам:

= 0,835 показывает, что средняя себестоимость изделия в отчетном периоде по сравнению с базисным периодом снизилась на 16,5 % за счет снижения себестоимости единицы продукции на отдельных заводах (см. в таблице ) и за счет структурных сдвигов, т.е. увеличения доли продукции в отчетном периоде с низкой себестоимостью (см. в таблице и ).

= 0,873 означает, что средняя себестоимость изделия в отчетном периоде по сравнению с базисным периодом снизилась на 12,8 % за счет снижения ceбeстоимости на отдельных заводах (см. в таблице .).

= 0,957 показывает, что средняя себестоимость изделия в отчетном периоде по сравнению с базисным снизилась на 4,3 % за счет снижения структурных сдвигов, т.е. за счет увеличения в отчетном периоде доли продукции с низкой себестоимостью (см. в таблице графу – «структура»).

Система взаимосвязанных индексов строится с целью выявления влияния отдельных факторов на изменение заработной платы.

или

,

где ФЗП - фонд заработной платы рабочих,

к - численность рабочих,

з - средняя заработная плата рабочего,

- индекс заработной платы переменного состава, показывающий изменение средней заработной платы рабочих за счет изменения, как индивидуальных уровней заработной платы, так и удельного веса рабочих с разным уровнем заработной платы, т.е. за счет структурных сдвигов,

- индекс заработной платы постоянного состава, отражающий изменение средней заработной платы за счет изменения индивидуальных уровней заработной платы,

- индекс структурных сдвигов характеризует изменение средней заработной платы за счет структур­ных сдвигов, т.е. за счет изменения удельного веса отдельных групп рабочих с разными уровнями заработной платы.

Индекс средней заработной платы переменного состава ( ) засчитанный для отдельного предприятия, показывает изменение средней заработной платы рабочих и в результате изменения квалифицированного состава, которое обусловлено, например техническим прогрессом. Если I₃ рассчитан для всей промышленности, то он показывает изменение средней заработной платы за счет изменения средней заработной платы в отдельных отраслях промышленности и удельного веса отдельных отраслей (по числу рабочих) с разным уровнем заработной платы.

Задача 7. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ЗАВИСИМОСТЕЙ

По данным о стоимости основных производственных фондов и объеме валовой продукции нужно определить уравнение связи и тесноту связи. Связь предполагается линейной. Принимая для этой связи уравнение прямой линии, определим его параметры на основе метода наименьших квадратов, решив следующую систему линейных уравнений:

Расчеты указанных в системе уравнений сумм произведем в табличной форме.

;

Таблица 15 Вспомогательные расчеты построения линейной модели

Стоимость основных производственных фондов, млн. руб. Х	Объем валовой продукции, млн. руб. У	ху
1 2 3 4 5 6 7 8 9 10	20 25 31 31 40 56 52 60 60 70	20 50 93 124 200 336 364 480 540 700	1 4 9 16 25 36 49 64 81 100	400 625 961 961 1600 3136 2704 3600 3600 4900	19,4 25,0 30,6 36,2 41,8 47,4 53,0 58,6 64,2 69,8

Определим коэффициент эластичности:

Следовательно, с увеличением стоимости основных произведенных фондов на 1 млн. руб. объем валовой продукции уваливается в среднем на 5,6 млн. руб., или с увеличением стоимости основных производственных фондов на 1 % объем валовой продукции увеличивается на 0,69 %.

Рассчитаем величину линейного коэффициента корреляции:

, применив формулу:

.

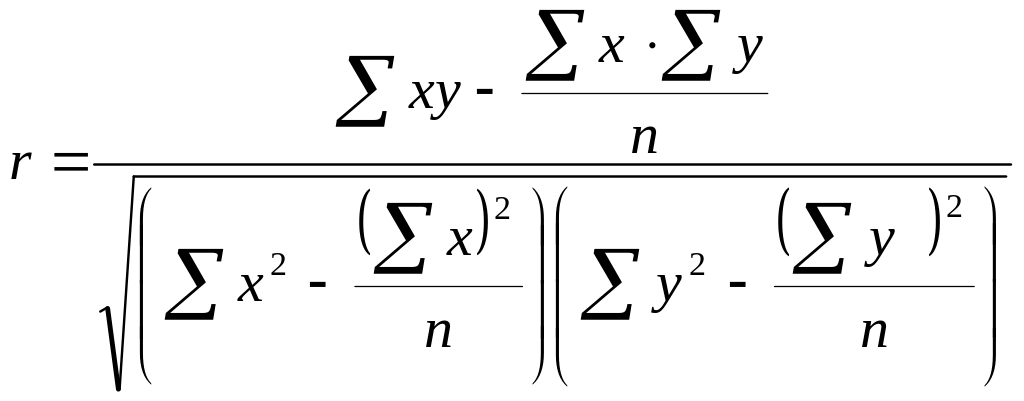Расчет коэффициентов регрессии несколько осложняется, если ряды по исследуемым факторам сгруппированы, а связь криволинейная.

Ниже приводятся базовые варианты заданий самостоятельных расчетных работ.

Студентам дневной, вечерней, сокращенной формы обучения и второго высшего образования необходимо согласовать номер варианта и числовые исходные данные с преподавателем дисциплины «Статистика».

Студенты заочной формы и дистанционного образования должны выполнять вариант, номер которого соответствует двум последним цифрам номера зачетной книжки студента.

Для всех студентов, выполняющих задание, предусмотрены консультации преподавателя дисциплины и время на защиту расчетных заданий.