Краткий курс лекций по дисциплине «Элементы высшей математики» Элементы теории вероятностей

Вопросы для изучения:

1. Случайные события.

2. Вероятность события.

3. Теоремы сложения и умножения вероятностей.

4. Формула полной вероятности и формула Байеса.

5. Случайные величины.

6. Распределение Пуассона.

7. Функция распределения вероятностей случайной величины.

8. Плотность распределения вероятностей случайной величины.

9. Числовые характеристики непрерывных случайных величин.

1. Случайные события

Теория вероятностей занимается изучением закономерностей случайных событий и случайных величин при массовом их появлении.

 Под случайным событием в теории вероятностей понимается событие, которое в результате опыта (испытания) может произойти или не произойти.

Событие называется достоверным, если оно обязательно произойдет в результате испытания, и невозможным, если оно не может произойти в результате испытания. Так при подбрасывании монеты достоверным является появление орла или решки и невозможным – появление кирпича.

События называются несовместными, если они не могут наблюдаться в одном и том же испытании одновременно. Так при бросании монеты появление орла или решки – несовместные события.

Суммой событий называется событие, состоящее в появлении хотя бы одного из этих событий.

 Произведением событий называется событие, состоящее в одновременном появлении всех этих событий.

 События являются равновозможными, если по условиям испытания нельзя считать, что одно из них может быть более возможным, чем другое.

2. Вероятность события

 Количественной мерой возможности появления события является вероятность. Наиболее широкое распространение имеют два определения вероятности события: классическое и статистическое.

 

Классическое определение вероятности связано с понятием элементарного события, благоприятствующего данному событию A.

 

Каждое событие является или элементарным, или может быть составлено из элементарных событий. Например, событие выпадения четного числа очков при бросании игральной кости, на которой нанесены цифры от 1 до 6, состоит из элементарных событий выпадения цифр 2, 4, 6. Таким образом, рассматриваемому событию благоприятствуют три элементарных события.

 

При классическом определении за вероятность события A принимается отношение числа элементарных событий, благоприятствующих событию A, к общему числу элементарных событий

,

где P(A) – вероятность события A, m – число элементарных событий, благоприятствующих событию A, n – общее число элементарных событий.

 

Статистическое определение вероятности связано с понятием относительной частоты события. Относительная частота события вычисляется по формуле:

,

где 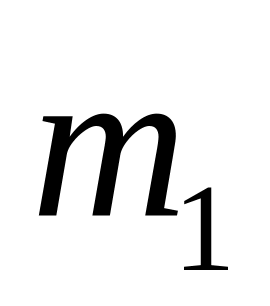– число появления события A в серии из 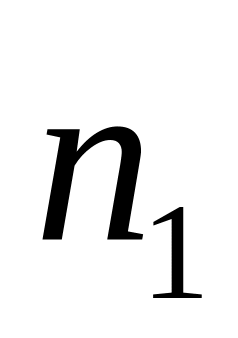опытов.

С увеличением числа опытов относительная частота обычно стабилизируется около некоторой постоянной величины.

 

При статистическом определении вероятности за вероятность события A принимают то число, относительно которого стабилизируется относительная частота при увеличении числа опытов.

Из определения вероятности события следует, что .