3) Генеральная дисперсия.

Для того чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.

Генеральной дисперсией D_г называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения.

Если все значения признака генеральной совокупности объема N различны, то

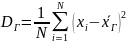
Если же значения признака имеют соответственно частоты N₁, N₂, …, N_k, где N₁ +N₂+…+N_k= N, то

Кроме дисперсии для характеристики рассеяния зна­чений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой — средним квадратическим отклонением.

Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:

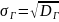
4) Выборочная дисперсия.

Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения, вводят сводную характеристику - выборочную дисперсию.

Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Если все значения признака выборки различны, то

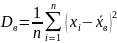
 если же все значения имеют частоты n₁, n₂,…,n_k, то

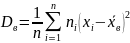
Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.

Выборочным средним квадратическим отклоненим называют квадратный корень из выборочной дисперсии:

Так же, как в теории случайных величин, можно доказать, что справедлива следующая формула для вычисления выборочной дисперсии: .

Пример 1. Найдем числовые характеристики выборки, заданной статистическим рядом

xi	2	5	7	8
ni	3	8	7	2

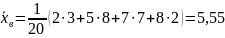
Замечание 1: если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.

Замечание 2. Если первоначальные варианты большие числа, то целесообразно вычесть из всех вариант одно и то же число С, равное выборочной средней или близкое к ней, т. е. перейти к условным вариантам u_i=x_i-C (дисперсия при этом не изменится). Тогда

Замечание 3. Если первоначальные варианты являются десятичными дробями с k десятичными знаками после запятой, то, чтобы избежать действий с дробями, умножают первоначальные ва­рианты на постоянное число С =10^k, т. е. переходят к условным вариантам u_i=Cx_i. При этом дисперсия увеличится в С² раз. Поэтому, найдя дисперсию условных вариант, надо разделить ее на С²:

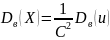
5) Исправленная дисперсия.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно

,

где D_Г – истинное значение дисперсии генеральной совокупности.

Для исправления выборочной дисперсии достаточно умножить ее на дробь

В качестве оценки генеральной дисперсии принимают исправленную дисперсию s², вычисляемую по формуле

.

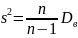Такая оценка будет являться несмещенной. Ей соответствует исправленное среднее квадратическое отклонение .

Замечание: формулы для вычисления выборочной дисперсии и исправленной дисперсии отличаются только знаменателями. При достаточно больших n выборочная и исправленная дисперсии мало отличаются, поэтому на практике исправленной дисперсией пользуются, если n<30.

Пример

xi	1	2	3	4
n1	20	15	10	5

6) Коэффициент вариации применяют для сравнения вариации признаков сильно отличающихся по величине, или имеющих разные единицы измерения (разные наименования).

На практике считают, что если 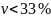  33 % , то совокупность однородная.

7) Модой M₀ называют варианту, которая имеет наиболь­шую частоту.

варианта	1	4	7	9
частота	5	1	20	6

M₀= 7.

8) Медианой т_e называют варианту, которая делит ва­риационный ряд на две части, равные по числу вариант. Если число вариант нечетно, т. е. n=2k+1, то m_e=x_k+1,

при четном п=2k медиана

Например, для ряда: 2 3 5 6 7 т_e= 5;

для ряда: 2 3 5 6 7 9

медиана равна т_e=(5+6)/2=5,5