1.3. Графическое представление вариациионого ряда

Для наглядного представления о поведении исследуемой случайной величины в выборке можно строить различные графики.

П олигон частот: ломаная, отрезки которой соединяют точки с координатами (x₁, n₁), (x₂, n₂),…, (x_k, n_k), где x_i откладываются на оси абсцисс, а n_i – на оси ординат. Если на оси ординат откладывать не абсолютные (n_i), а относительные (w_i) частоты, то получим полигон относительных частот

Пример:

xi	1	4	5	7
ni	20	10	14	6

Г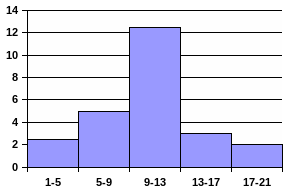 истограмма – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высотами – отрезки длиной n_i /h (гистограмма частот) или  w_i /h (гистограмма относительных частот). В первом случае площадь гистограммы равна объему выборки, во втором – единице.

Пример:

xi-xi+1	1-5	5-9	9-13	13-17	17-21
ni	10	20	50	12	8
	2,5	5	12,5	3	2

Кумулятивные ряды графически изображают в виде кумуляты. Для ее построения на оси абсцисс откладывают варианты признака или интервалы, а на оси ординат – накопленные частоты F( ) или относительные накопленные частоты, а затем точки с координатами ( _i ; F ( _i )) или ( _i ;  ) соединяют отрезками прямой. В теории вероятностей кумуляте соответствует график интегральной функции распределения .

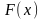Имеется распределение 80 предприятий по числу работающих на них (чел.). Найти накопленные частоты F(x_i) и построить кумуляту.

i	1	2	3	4	5	6	7
xi	150	250	350	450	550	650	750
ni	1	3	7	30	19	15	5
F(xi)	1	4	11	41	60	75	80

На рисунке показана кумулята распределения предприятий по числу работаю­щих (чел.).

Полигон распределения. На графике ѕ это кривая, отражающая по оси абсцисс (Х) средние значения классов, а по оси ординат (Y ) ѕ частоту накопления величин в каждом классе.

Гистограмма распределения. График, выполненный в прямоугольной системе координат и отражающий по оси ординат (Y) частоту накопления величин в классе, а по оси абсцисс (Х) - границы классов.

Графическое представление результатов измерений не только существенно облегчает анализ и выявление скрытых закономерностей, но и позволяет правильно выбрать последующие статистические характеристики и методы.

Если гистограмма и полигон по своему виду близки к виду графика нормального распределения, то группа однородна.

Если графики низкие и растянутые, то группа возможно однородна, но не компактна.

Если графики имеют две и более вершины, то группа неоднородна по данному признаку и ее необходимо разбить на группы.