Лекция № 16.

Тема: раскраска графов и карт

Основные вопросы, рассматриваемые на лекции:

1. Раскраска графа. Хроматическое число графа. Теорема Кенига.

2. Раскраска карты. Проблема 4-х красок.

3. О решении проблемы 4-х красок.

Краткое содержание лекционного материала

1. Раскраска графа. Раскраска карты. -раскраска графа – это приписывание цветов его вершинам, такое, что две любые смежные вершины окрасятся в разные цвета. Граф называется -раскрашиваемым, если его можно окрасить не более чем в цветов. Хроматическим числом графа называется наименьшее число цветов, для которого граф имеет -раскраску. Граф называется -хроматическим, если . Граф являеется -раскрашиваемым, если .

Если граф 1-раскрашиваем, то он вполне несвязен, т.е. не содержит ребер. Значит, тогда и только тогда, когда граф вполне не связан.

тогда и только тогда, когда граф не содержит нечетных простых циклов (терема Кенига). Треугольник и являются примерами 3- и 4- хроматического графа. не является примером 5- хроматического графа, так как мы рассматриваем только плоские графы. Можно доказать следующую теорему: каждый плоский граф 5-раскрашиваем.

Гипотеза: каждый ли граф 4-раскрашиваем?

2. Раскраска карт. Раскраской плоской карты называется такое приписывание цветов его областям, что никакие две смежные области не получают одинакового цвета. Карта называется -раскрашиваемым, если существует его раскраска, использующая не более чем в цветов. Можно доказать, что каждая плоская карта 5-раскрашиваема.

В 1852 году Френсис Гутри (Guthrie), составляя карту графств Англии, обратил внимание, что для такой цели вполне хватает четырех красок. Его брат, Фредерик, сообщил об этом наблюдении известному математику О. Де Моргану (DeMorgan), а тот - математической общественности. Точная формулировка гипотезы опубликована А. Кэли (Cayley, 1878).

Проблема 4-х красок: достаточно ли 4-х красок для раскраски любой плоской карты.

Заметим, что нетрудно доказать: гипотеза «каждый граф 4-раскрашиваем» равносильна гипотезе 4 красок «каждая плоская карта 4-раскрашиваема».

3. О решении проблемы 4-х красок. В 1976 г К. Аппель и В. Хакен доказали, что четырьмя красками можно раскрасить любую карту. Их доказательство очень объемное, опирается на алгоритмы, реализуемые на компьютерах, в нем все вычисления человеку невозможно проверить.

Лекция № 17.

Тема: кратчайшие пути. Алгоритм Дейкстры

Основные вопросы, рассматриваемые на лекции:

1. Задача о кратчайшем пути на графе.

2. Определение алгоритма Дейкстры.

3. Выполнение алгоритма Дейкстры на примере графа.

Краткое содержание лекционного материала

1. Задача о кратчайшем пути на графе. Припишем всем ребрам графа веса – положительные числа. Кратчайший путь от вершины до вершины – это маршрут от до с минимальной суммой весов ребер маршрута. Надо найти все кратчайшие пути от данной вершины до всех остальных вершин.

Пример. Маршрут имеет сумму весов ребер 13, а маршруты и – 14. Значит, – кратчайший путь от до .

Задача о кратчайшем пути на графе решается алгоритмом, изобретенным нидерландским ученым Э. Дейкстрой в 1959 г.

Расстоянием от до называют сумму весов ребер по одному из маршрута от до .

2. Определение алгоритма Дейкстры. Каждой вершине ставим метку – минимальное известное расстояние от данной вершины .

Алгоритм работает пошагово – на каждом шаге он «посещает» одну вершину и пытается уменьшить метку вершины. Если все вершины посещены, алгоритм завершается.

Метка вершины равна 0. В начале метки остальных вершин предполагаются равными . Иначе, из ещё не посещённых вершин выбирается вершина , имеющая минимальную метку. Рассматривают всевозможные маршруты с началом , в которых является предпоследним пунктом.

Для каждой не посещённой вершины , смежной с вершиной , находят сумму значения текущей метки и веса ребра, соединяющего и . Если полученная сумма  меньше значения  метки , то метку  заменяют меткой .

Рассмотрев все не посещённые вершины, смежные с вершиной , вершина отмечается как посещенная, и повторяется шаг алгоритма.

4. Выполнение алгоритма Дейкстры на примере графа. Требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.

Кружками обозначены вершины, линиями – ребра графа. В кружках обозначены номера вершин, над ребрами обозначена их вес – (или длина пути).

Рядом с каждой вершиной обозначена метка – длина кратчайшего пути в эту вершину из вершины 1.

Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.

7, поэтому метка  при вершине 2 заменяется меткой 7,

9, поэтому метка  при вершине 3 заменяется меткой 9,

14, поэтому метка  при вершине 6 заменяется меткой 14,

вершина 1 вычеркивается из числа посещенных вершин.

710179, поэтому метка 9 при вершине 3 остается;

71522, поэтому метка  при вершине 4 заменяется меткой 22;

вершина 2 вычеркивается из числа посещенных вершин.

9112022, поэтому метка 22 при вершине 4 заменяется меткой 20;

921114, поэтому метка 14 при вершине 6 заменяется меткой 11;

вершина 3 вычеркивается из числа посещенных вершин.

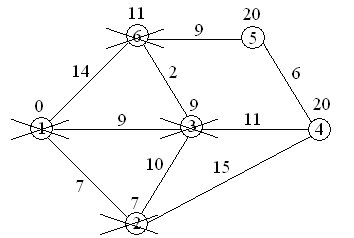
11920, поэтому метка  при вершине 5 заменяется меткой 20;

вершина 6 вычеркивается из числа посещенных вершин.

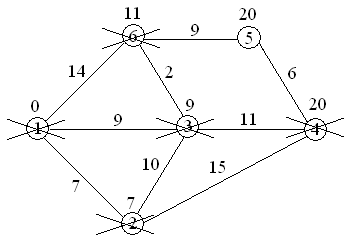
2062620, поэтому метка 20 при вершине 5 остается;

вершина 4 вычеркивается из числа посещенных вершин.

У вершины 5 не посещенных смежных вершин нет, поэтому вершина 5 также вычеркивается из числа не посещенных вершин.

Алгоритм заканчивает работу, так как нельзя больше обработать ни одной вершины. Кратчайшие пути – это последние метки при вершинах.