Лекция № 15.

Тема: Деревья. Остов графа

Основные вопросы, рассматриваемые на лекции:

1. Эквивалентные определения дерева.

2. Пример. Деревья с числом вершин не больше 5.

3. Остов графа. Поиск в ширину и в глубину.

Краткое содержание лекционного материала

1. Эквивалентные определения дерева. Дерево – это связный граф, в котором нет циклов. Следующая теорема показывает только меньшую часть возможных равносильных определений дерева.

Теорема 1. Пусть – -граф. Тогда следующие условия эквивалентны:

( ) – дерево;

( ) любые две вершины в графе соединены единственной простой цепью;

( ) – связный граф и ;

( ) –граф без циклов и .

Доказательство. ( )( ). Так как – связный граф, то любые две вершины и в графе соединены цепью, простой, поскольку еще –граф без циклов.

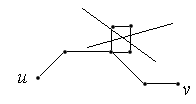
Если вершины и соединены двумя цепями, то получится цикл:

( )( ). Непосредственно по условию граф связный. Доказываем равенство

(1)

индукцией по числу ребер (или вершин).

Уберем одно ребро между вершинами и . В силу единственности соединяющей цепи между вершинами и , граф распадается на два графа, удовлетворяющих условию ( ).

Если эти графы имеют по и вершин и по и ребер, то по индуктивному предположению для них выполняется равенство (1):

(2)

(3)

Сложив по частям (2) и (3), учитывая, что и , то получим равенство (1).

( )( ). Допустим, что граф содержит цикл, можно считать, что простой цикл с вершинами и ребрами. Остальные вершин соединяются с этим циклом некоторым ребром, причем все такие ребра попарно различные.

Получается, что граф имеет число ребер , что противоречит (1).

( )( ). В связной компоненте графа без циклов, мы, удаляя по одной крайней вершине и инцидентному ей ребру, на финише, в силу (1), получим одну вершину.

Если граф не связный, то он распадается на связные компоненты. Указанный выше процесс показывает, что тогда вершин будет больше ребер не на 1, а на . Значит, граф не может быть не связным.

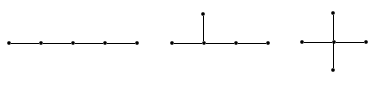
2. Пример. Деревья с числом вершин не больше 5. Приведем все попарно неизоморфные деревья с числом вершин, не больше 5:

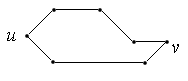
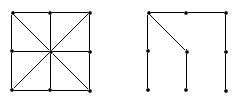
3. Остов графа. Поиск в ширину и в глубину. Остов графа – это подграф графа, содержащий все его вершины и являющийся деревом.

Приведем пример графа и одного из его остовов:

Обходы всех вершин графа совершаются как обход некоторого его остова. Методами обхода графа являются поиск в глубину и поиск в ширину.

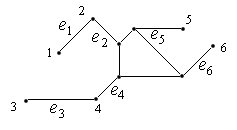
Алгоритм поиска в глубину: для каждой не пройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них.

Пример графа и поиска в глубину этого графа:

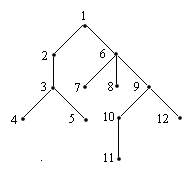
1-2-3-4-3-5-3-2-1-6-7-6-8-6-9-10-11-10-9-12-9-6-1.

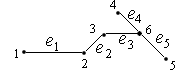
Порядок поиска в ширину: началу обхода приписывается метка 0; вершинам, смежным с вершинами метки i, – метка i1 (i0,1,2,…). Затем нумеруем вершины: вначале вершины с меткой 0, затем с меткой 1 и т. д.

Пример графа и поиска в ширину этого графа: