2.4. Аналитический метод
Достоинство аналитических методов заключается в первую очередь в высокой точности определения исследуемых характеристик в каждое мгновение промежутка времени действия механизма. Сущность рассматриваемого метода заключается в преобразовании координат какой-либо точки при последовательном переходе из одной системы координат в другую. Среди многочисленных методов кинематического анализа механизмов широкое распространение приобретают методы, которые позволяют ввести в обращение матрицы и производить с их помощью соответствующие действия. Такие методы отличаются простотой алгоритмизации исследования характеристик движения и реализации на ПЭВМ.
2.4.1. Преобразование координат точки в плоских механизмах
Пусть даны системы плоских прямоугольных координат X0Y0 и X1Y1 (рис.1). Положение начала системы координат X1Y1 определяется в системе координат X0Y0 величинами a и b. Относительный поворот координатных осей – направляющими косинусами mkl (k, l = 1,2).
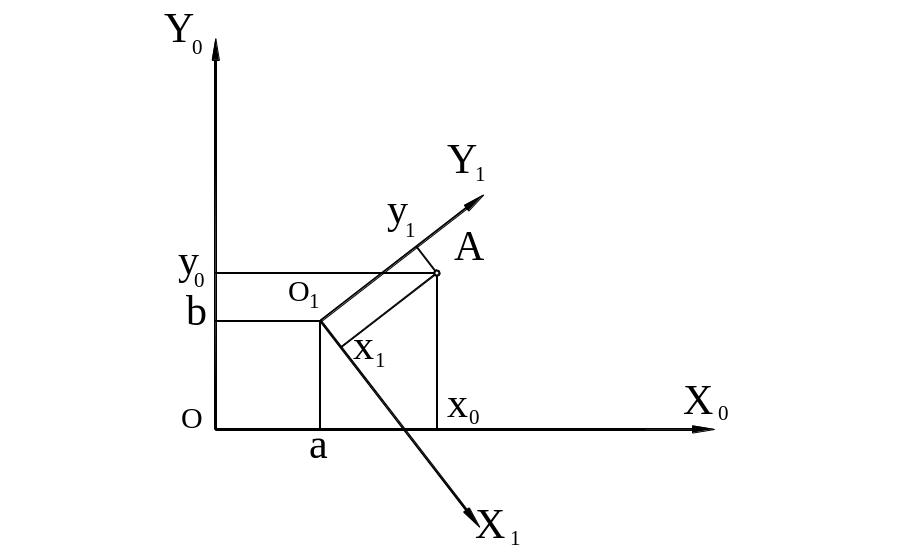
Рис. 2.13. Схема расположения систем координат
Как известно, преобразование координат какой-либо точки из системы X1Y1 в систему X0Y0 в общем случае относительного движения систем координат в плоскости определяется уравнениями вида:
x0 = a + x1 m11 + y1 m12 , ( 1 )
y0 = b + x1 m21 + y1 m22 , (2.15)
где x1, y1 - координаты точки в системе X1Y1 ;
x0, y0 - координаты точки в системе X0Y0 ;
a, b - координаты точки O1 в системе X0Y0 ;
m11 = cos (X0^X1); m12 = cos (X0^Y1); m21 = cos (Y0^X1);
m22 = cos (Y0^Y1) - направляющие косинусы.
Система уравнений (2.15) может быть записана в эквивалентной матричной форме:
=
+
,
где = X0 - матрица-столбец координат точки в системе X0Y0;
= X1 - матрица-столбец координат точки в системе X1Y1;
= L10 - матрица-столбец параллельного переноса начала координат системы X1Y1 в начало координат системы X0Y0;
= V10 – квадратная матрица поворота системы координат X1Y1 относительно системы X0Y0 .
Получим X0 = L10 + V10 X1 .
В общем виде X i - 1 = Li , i - 1 + Vi , i - 1 X i (2.16)
Последовательные преобразования ряда систем координат производятся следующим образом. Пусть, например, необходимо произвести преобразования координат точки А из системы X3Y3 в систему X2Y2 , затем в систему X1Y1 и далее в систему X0Y0 (рис. 2.14).
Рис. 2.14. Схема расположения точки в координатных системах
Согласно выражению (2.16) составляем уравнение преобразования системы X3Y3 в систему X2Y2 :
X2 = L32 + V32 X3 ;
системы X2Y2 в систему X1Y1 :
X1 = L21 + V21 X2 ;
системы X1Y1 в систему X0Y0 :
X0 = L10 + V10 X1 .
Объединив эти выражения, получим
X0
= L10
+ V10
L21
+ V21
L32
+
V32
X3
.
В общем виде
X0 = L10 + V10 … Ln-1, n-2 + Vn-1, n-2 Ln,n-1 + Vn,n-1 Xn . (2.17)
Полученные результаты распространяются на замкнутые и незамкнутые кинематические цепи. Замкнутые кинематические цепи могут быть одно- и многоконтурными. Какова бы ни была одноконтурная кинематическая цепь, с каждым ее звеном связывается система координат XiYi ( i = 1, 2, 3, … , n, где n – число звеньев).
Если произвести последовательные преобразования систем координат вдоль замкнутого контура звеньев, начиная с некоторого звена или, иначе говоря, с некоторой системы координат, и вернуться к исходному звену (к исходной системе координат), то такое преобразование будет являться тождественным. Уравнение (2.17) является уравнением замкнутости контура кинематической цепи.
В кинематических цепях плоских механизмов наибольшее распространение получили кинематические пары 5 класса: поступательные и вращательные. Рассмотрим преобразование систем координат в этих кинематических парах.
На рис. 3 представлено схематическое изображение поступательной кинематической пары, образованной звеньями i-1 и i, с которыми связаны плоские системы координат Xi-1Yi-1 и XiYi . Соответствующие координатные оси параллельны.
Рис. 2.15. Поступательная кинематическая пара
Уравнение преобразования координат из системы XiYi в систему Xi-1Yi-1 будет аналогично выражению (2). Матрицы Vi,i-1 и Li,i-1 будут иметь следующий вид:
Vi,i-1
=
=
=
=
;
Li,i-1 = .
Получаем уравнение преобразования в матричной форме:
=
+
=
.
На рис. 2.16 представлено схематическое изображение вращательной кинематической пары, составленной звеньями i-1 и i. Со звеньями связаны системы координат Xi-1Yi-1 и XiYi . Оси Xi-1 и Xi направлены вдоль соответствующих звеньев. Начало координат Оi системы XiYi расположено в центре кинематической пары.
Рис. 2.16. Вращательная кинематическая пара
Угол
-
угол поворота в кинематической паре.
Уравнение преобразования координат во
вращательной паре также соответствует
выражению (2.16). Матрицы Vi,i-1
и Li,i-1
будут
иметь следующий вид:
Vi,i-1=
=
;
Li,i-1
=
.
Получаем уравнение преобразования в матричной форме:
=
+
=
При рассмотрении вращательной пары удобно начала координат Оi-1 и Оi совмещать с центром пары (рис. 5). Тогда матрица Vi-1 будет иметь прежний вид, а матрица Li,i-1 будет равна 0.
Li,i-1
=
.
Рис. 2.17. Вращательная кинематическая пара
(оси координат расположены в центре пары)
Уравнение преобразования в матричной форме будет определяться следующим образом:
=
=
.