Методические указания к выполнению лабораторной работы № 3

Для решения математических задач, представленных в лабораторной работе необходимо вспомнить следующий теоретический материал.

1. Задача вычисления длин сторон многоугольника, заданного координатами его вершин сводится к задаче нахождения длины отрезка, заданного координатами его концов.

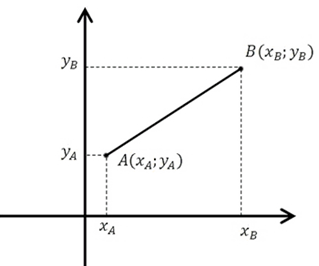
Как вы видите из рисунка, длина отрезка — это длина гипотенузы в прямоугольном треугольнике с катетами равными: Х_В – Х_А     и    У_В – У_А.

Формула для определения длины отрезка, если известны координаты его концов:

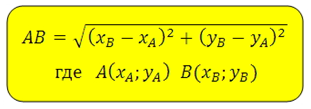
2. Задача нахождения углов треугольника, если известны координаты его вершин, решается с помощью теоремы косинусов.

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними:

a² = b² + c² — 2bc · cos α

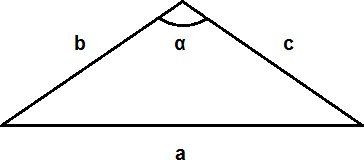
Из формулировки теоремы, очевидно, что для нахождения косинуса исходного угла необходимо знать длины сторон треугольника. (Смотреть предыдущую задачу.)

Чтобы вычислить величину угла, зная значение косинуса угла, используют обратную тригонометрическую функцию арккосинус – ACOS. (В Excel результат функции ACOS – угол, выраженный в радианах.)

Для проверки правильности решения задачи вычислить сумму углов треугольника.

3. Задача определения попадания точки внутрь заданной области решается нахождением уравнений графиков функций, которые ограничивают область и определением условий, при которых точка будет находиться внутри области.

Например: определить условия, при которых точка будет принадлежать заштрихованной области.

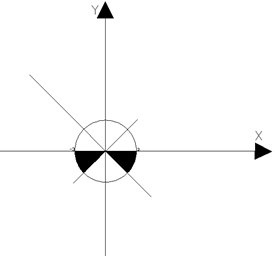
Для определения условий мы должны записать уравнения графиков функций, ограничивающих заданную область: прямой X, двух прямых, проходящих через начало координат и окружности.

Очевидно, что это . Из последнего уравнения следует выразить .

Запишем условия для области, находящейся слева от оси Y:

.

Условия для области, находящейся справа от оси Y:

.

Составим блок-схему решения этой задачи, используя выписанные нами условия:

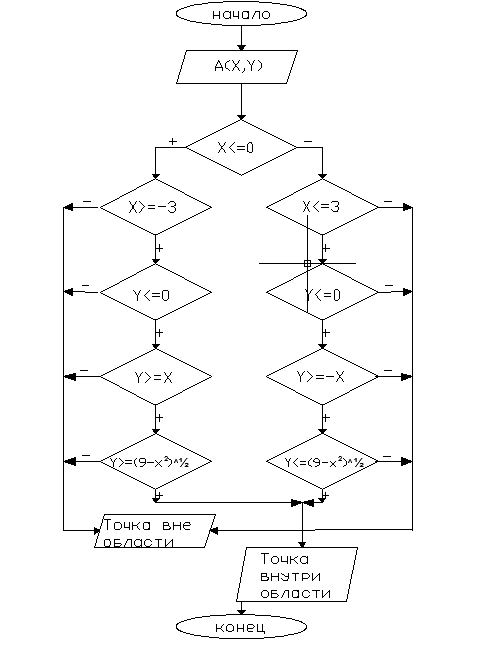
Табличный процессор Microsoft® Excel

Функции рабочего листа

Главный инструмент при работе с электронными таблицами – клеточные функции.

Пиктограмма f(x) открывает окно Мастера функций, предлагающее быстрый поиск функции рабочего листа. Рассмотрим некоторые из математических функций.

Математические функции Функция суммирования

Функция имеет следующий формат:

СУММ(<число1>;<число2>; ...) - возвращает сумму чисел, входящих в список аргументов. Список может содержать до 30 элементов. Если в суммируемом блоке встречаются нечисловые элементы, они участвуют в суммировании как нули.

Примеры: СУММ(3;2)=3+2=5,

СУММ(А1 ;2; А2:СЗ)=А1 +2+А2+В2+С2+АЗ+ВЗ+СЗ.

Функцию суммирования, можно ввести с кла­виатуры или с помощью пиктограммы Авто суммирование ∑.

Функция суммирования аналогична простому перечислению слагаемых со знаком плюс.