1.3. Частота вращения эллиптического поля

На рис. 1.2. показаны векторы прямо и обратно вращающихся МДС (F₁ и F₂), а также вектор результирующей МДС (F_Р) в различные моменты времени. Из рисунка видно, что большая ось эллипса равна удвоенной сумме, а малая ось удвоенной разности магнитодвижущих сил F1 и F2: a = 2(F₁ + F₂); b = 2(F₁ – F₂).

Из последнего выражения легко увидеть, что при равенстве нулю одной из МДС (F₁ или F₂), поле становится круговым, а при равенстве МДС друг другу (F₁ = F₂) оно превращается в пульсирующее, т.е. эллипс вырождается в линию.

Рис. 1.2. К вопросу о частоте вращения эллиптического поля

Будем фиксировать через каждые 1/8·Т прямо и обратно вращающиеся МДС F₁ , F₂ и их сумму F_p. За одно и то же время векторы F₁ и F₂ каждый раз будут поворачиваться на углы ± 45º, а их сумма F_p первый раз повернется на угол γ₁, второй раз на угол γ₂ и т.д. Из рис. 1.2 видно, что γ₁< γ₂, а поскольку временные отрезки одинаковые, это означает, что F_p вращается с переменной частотой.

Следовательно, эллиптическое магнитное поле вращается с переменной угловой частотой: большей возле малой оси эллипса и меньшей возле большой оси эллипса.

Исследованиями установлено [1], что

, (1.7)

где: k = (F₁ – F₂)/(F₁+ F₂) – коэффициент формы эллипса.

Используя формулу (1.7), найдем максимальные и минимальные значения мгновенной скорости вращения эллиптического поля.

Рис. 1.3. Осциллограмма мгновенной скорости эллиптического поля.

Минимум скорости имеет место при = 0 и = 180^о , т.е. когда вектор F совпадает с большей осью а эллипса. Максимум скорости – когда вектор F совпадает с меньшей осью в эллипса. Выражения максимальной и минимальной скоростей можно найти, подставив в (1.7) соответственно значения sin = 1 и sin = 0:

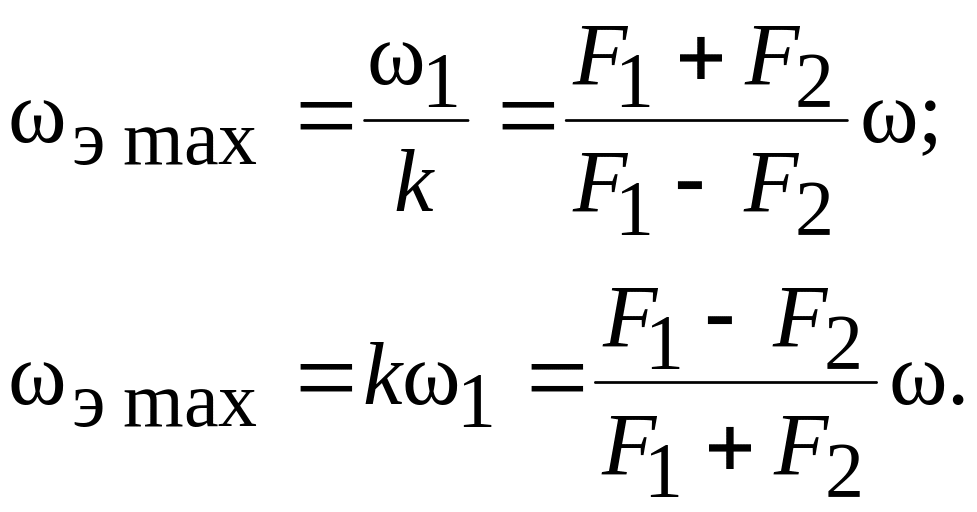
На рис. 1.3 показана осциллограмма мгновенной скорости вращения эллиптического поля при отношении .

Эллиптическое поле вызывает неодинаковое насыщение участков    магнитной    цепи   (где   поле    больше, там и  насыщение

больше), неодинаковые потери в стали, неодинаковые нагревы этих участков, магнитострикционные шумы.

1.4. Получение кругового вращающегося магнитного поля в несимметричных двухфазных микромашинах

Эллиптическое магнитное поле станет круговым, если одна из составляющих, например F₂, будет равна 0:

(1.8)

Формула (1.8) справедлива, если:

1)  ;

2) cos(θ + β) = -1.

Отсюда вытекают два условия получения кругового магнитного поля в несимметричных двухфазных микромашинах:

1) амплитуды магнитодвижущих сил должны быть равны по величине, т.е. F_mA = F_mB = F_m;

2) сумма углов их пространственного и временного сдвига должна быть равна 180º , т. е. θ + β=180º.

Так как θ + β=180º , то в формуле (1.5) cos(θ - β) = - cos 2β или cos(β - θ) = - cos 2θ. Тогда величина круговой МДС будет

. (1.9)

Анализ формулы (1.9) показывает, что магнитное поле хотя и круговое, но не максимальное, если углы θ и β каждый в отдельности не равен 90º.

Задача 1.4. Определить, во сколько раз величина круговой МДС при θ = 100^о и β = 80^о отличается от значения при θ = β = 90^о.

1.5. Пусковые моменты несимметричных двухфазных микромашин

Известно, что пусковые моменты асинхронных и синхронных двигателей при асинхронном пуске пропорциональны квадрату фазного напряжения, т. е. M_п ~ U ².

Поскольку U ≈ E = 4,44·f·w·k_об·Ф_m , то при отсутствии насыщения   магнитной цепи Ф ~ F, U ~ F,  следовательно, 

M_п = c· (F₁² - F₂² ),

где c – коэффициент пропорциональности;

w – число витков обмотки статора;

f – частота питающей сети;

k_об – обмоточный коэффициент.

Подставляя (1.5), (1.6) в последнее равенство, получим:

С учетом того, что cos(θ - β) = -cos(θ + β) = 2sinθ sinβ,

окончательно будем иметь:

. (1.10)

Следовательно, пусковой момент несимметричного двухфазного двигателя пропорционален произведению амплитуд магнитодвижущих сил и синусам углов их пространственного и временного сдвигов. Важно отметить, что максимум момента будет при θ = 90º и β = 90º.