1.1. Обобщенная структура кг

КГ – это класс семантических сетевых моделей, структурно представляющий собой ориентированные двудольные графы с двумя типами узлов – узлами-концептами (сущностями) и узлами-отношениями. Дуги концептуальных графов не несут иной смысловой нагрузки, кроме указания на наличие связи между узлами и на порядок рассмотрения связей при интерпретации модели. Любая дуга (связь, ссылка) в КГ связывает один из узлов-отношений с одним из узлов-концептов (т. е. связи между однотипными узлами не допускаются). В графе могут присутствовать узлы-концепты, не имеющие связей, но не может быть связей, не присоединенных к двум узлам. Три вида КГ имеют предопределенные названия. Это «бланк» (пустой граф без узлов и дуг), «синглетон» (граф, состоящий из одного узла-концепта) и «звезда» (граф, содержащий один узел-отношение и произвольное число связанных с ним узлов-концептов).

Концепты в КГ представляют собой любые сущности (объекты, свойства, величины, процессы, события и т. п. или их типы) и характеризуются типом концепта и референтом (или денотатом – содержательным описанием). При этом абстрактный синтаксис не регламентирует форм представления для типа и референта. В нотации CGIF и ряде других текстовых нотаций описание концепта помещается в квадратные скобки. Тип и референт в описании концепта разделяются двоеточием. Соответственно, концепт [student: Ivanov] имеет тип student и денотат Ivanov (предмет данного типа). Концепт [student] обозначает неопределенный объект типа student, а [‘Ivanov’] (или [:Ivanov]) – концепт универсального типа («Entity» – «сущность»). В графической нотации DF концептам соответствуют прямоугольники.

Отношения (концептуальные отношения) в КГ характеризуются типом отношения и положительным целым числом n, называемым валентностью, которое обозначает количество связей, присоединенных к данному узлу. Дуги при этом нумеруются числами от 1 до n, а само отношение считается n-арным. Первые n – 1 дуг, связанных с отношением, считаются входящими, а последняя n-я дуга – исходящей. Последовательность t₁, ..., t_n типов концептов, связанных с данным отношением, называется сигнатурой отношения. Все отношения, имеющие одинаковый тип, имеют соответственно одинаковые сигнатуры и валентности. Специфическим видом отношений в КГ являются акторы, которые представляют собой отношения с неопределенным в текущем контексте назначением (смыслом), непредставимым в стандартных нотациях или описанным вне графа. Однако с точки зрения структурной организации графа акторы ничем не отличаются от обычных отношений. В текстовых нотациях КГ отношения выделяются круглыми скобками (акторы в CGIF – треугольными скобками), а в DF – овалами (акторы – ромбами).

На рис. 1.1 в графической форме (DF) представлен пример КГ для описания ситуации «Иванов добирается до работы на метро». В примере использованы традиционно принятые обозначения отношений «быть агентом действия» («Agnt»), «быть целью действия» («Dest») и «быть инструментом действия» («Inst»). В концептах «Work» и «Metro» определен только тип концепта, а в концепте «Person: Ivanov» – и тип, и референт.

Рис. 1.1. DF для ситуации «Иванов добирается до работы на метро»

Для примера на рис. 1.1 текстовые описания в различных нотациях КГ выглядят следующим образом:

а) в нотации LF:

[Go]-

(Agnt)[Person: Ivanov]

(Dest)[Work]

(Inst)[Metro];

б) в нотации KIF:

(exists ((?x Go) (?y Person) (?z Work) (?w Metro))

(and (Name ?y Ivanov)

(Agnt ?x ?y) (Dest ?x ?z) (Inst ?x ?w)));

в) в нотации CGIF:

[Go *x] (Agnt ?x [Person: Ivanov]) (Dest ?x [Work]) (Inst ?x [Metro])

В дальнейшем в качестве базовой формы текстового представления КГ будет использоваться стандартный формат CGIF.

При реализации описания ситуации на рис. 1.1 в CGIF для определения порядка связей между узлами КГ используется метка x – произвольный идентификатор, не сопоставляемый с какой-либо конкретной сущностью или отношением и служащий исключительно для формального указания на узел, участвующий в образовании той или иной дуги графа. При этом лексема «*х», называемая определяющей меткой, непосредственно приводится в описании самого узла-источника связи, а лексема «?х» (связанная метка) – в описаниях других узлов, связанных дугами с данным источником.

Как видно на рис. 1.1 в данном КГ все отношения имеют валентность 2. Если валентность каких-либо отношений превышает это значение, то в графической нотации (а также в линейной текстовой нотации LF) используется цифровая маркировка дуг, связанных с этими отношениями (рис. 1.2).

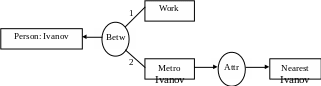
Рис. 1.2. Пример DF для случая отношения с валентностью 3

Здесь представлено графическое отображение ситуации «Иванов находится между работой и ближайшим метро» (отношение «находится между» обозначено через «Betw», а «иметь свойство (атрибут)» – через «Attr»). Подобная нумерация дуг отображается и в нотации LF. Для примера на рис. 1.2 описание в LF выглядело бы так:

[Person: Ivanov](Betw)-

1-[Work]

2-[Metro](Attr)[Nearest]

В нотации CGIF соответствующую ситуацию можно представить без использования нумерации:

(Betw [Work] [Metro *x] [Person:Ivanov]) (Attr ?x [Nearest])

1.2. λ-выражения и типизация концептов и отношений в КГ

Важным механизмом абстрагирования, обобщения и образования новых типов в аппарате КГ являются λ-выражения. n-арное λ-выражение представляет собой параметризованный КГ, в котором n концептов выступают в качестве формальных параметров графа. Эти параметры нумеруются (как дуги для узлов-отношений), а их типы образуют сигнатуру λ-выражения (как и в случае произвольного отношения). При этом в LF и DF символы λ_i (где i – номер соответствующего формального параметра выражения) используются вместо референтов концептов, сопоставляемых с параметрами. В CGIF λ-выражения представляют собой концептуальные отношения специального типа «lambda».

Пусть, например, требуется описать обобщенную ситуацию «Некий человек (Person) направляется в некоторый город (City)» (тогда ситуация «Иванов направляется в город Москву» будет частным случаем описанной ранее обобщенной ситуации, в котором параметры «Иванов» и «Москва» задают конкретный рассматриваемый случай).

Тогда соответствующий КГ в нотации LF выглядел бы так:

[Person: ₁](Agnt)[Go](Dest)[City: ₂]

В нотации CGIF эта общая ситуация может быть определена с использованием λ-выражения, имеющего сигнатуру <Person, City> и выглядящего следующим образом:

(lambda (Person*x, City*y) [Go *z] (Agnt ?z ?x) (Dest ?z ?y))

Здесь предопределенный символ «lambda» указывает именно на то, что далее будет описываться параметризованное λ-выражение. За ключевым словом «lambda» в круглых скобках следует список определений формальных параметров. Каждый элемент этого списка представляет собой пару <«тип», *«определяющая метка»>, где определяющая метка является именем формального параметра, которое может далее использоваться (с предварительным употреблением символа «?») при описании смыслового содержания λ-выражения (т. е. при описании тела λ-выражения). Служебные символы «*» и «?» соответственно позволяют различать декларацию формального параметра («*») и обращения к нему («?») при реализации описания тела λ-выражения.

Подобная способность КГ к гибкой параметризации используется не только для описания обобщенных, абстрактных суждений (которые могут конкретизироваться указанием фактических значений параметров λ-выражений), но и для образования новых типов концептов и отношений.

Для рассмотрения этих возможностей необходимо предварительно охарактеризовать общие принципы типизации концептов и отношений в КГ.

Типы концептов и отношений представляют собой самостоятельные сущности в модели КГ и образуют иерархии типов двух видов – иерархию типов концептов и иерархию типов отношений.

Иерархии типов – это частично упорядоченные множества, элементы которых называются метками типа. Метки типа могут быть либо примитивами (предопределенными или вводимыми аксиоматически, без пояснений), либо определяемыми (выражаемыми через примитивы). В нотации CGIF предопределенными примитивами в иерархии типов концептов являются метки «Entity» (абстрактный универсальный тип, т. е. тип всех типов, воспринимаемый как «тип по умолчанию») и «Absurdity» (абстрактный «абсурдный» тип, т. е. тип, являющийся подтипом всех остальных типов). Для любого типа концептов t справедливо утверждение Absurdity < t < Entity. В иерархии типов отношений в CGIF также введены предопределенные типы отношений, в частности – с метками «GT» («больше»), «LT» («меньше»), «EQ» («равно»). На основе этих отношений описываются в том числе и связи вида «тип – подтип» (подтип связывается с типом через отношение LT, а тип с подтипом – отношением GT) между различными типами, входящими в иерархии.

Определяемый (т. е. создаваемый в описании графа) тип в КГ может описываться некоторым λ-выражением, называемым определением типа. При этом определение и метка типа сопоставляются и становятся взаимозаменяемыми при интерпретации описания КГ. Приведем ряд примеров с использованием нотации CGIF.

Пример 1. Пусть требуется описать новый тип концептов с меткой «Т», имеющих смысл «житель города Москвы» (где «Москва» относится к типу «City», а отношение «жить в…» обозначается через «LiveIn»). Пусть также необходимо указать на то, что тип «житель Москвы» является подтипом типа «Человек» («Person»). Это можно сделать следующим образом:

[TypeLabel: Person *x]

[TypeLabel: Т *y] (Def [?y] [LambdaExpression: “(lambda (Person *z) (LiveIn ?z [City: Moscow]) )” ] )

(GT ?x ?y)

В приведенном тексте курсивом выделены предопределенные символы CGIF. Первая строка фрагмента описывает метку-примитив «Person». Далее следует непосредственное определение типа концептов с меткой «Т». Здесь используется предопределенный тип отношений «Def» (указание на декларацию нового типа) и предопределенный тип концептов «LambdaExpression» (указание на последующее приводимое в кавычках λ-выражение, раскрывающее семантическое содержание концептов данного типа). После многоточия в рассматриваемом CGIF-тексте следует описание упорядочивающего отношения, которое определяет иерархические отношения между типами. Предопределенный тип отношений «GT» указывает на то, что тип (в примере – «Person») и подтип («житель Москвы») не совпадают по множеству возможных значений и объекты подтипа образуют подмножество объектов типа (аналогично указанию на различие неравенств a < b и a ≤ b).

Если проанализировать приведенный CGIF-текст с точки зрения отображения некоторого КГ, то можно отметить, что фактически данный текст описывает граф из трех концептов, соответствующих типам «Person» и «T», а также λ-выражению, описывающему тип «Т» (в этом концепте заключенная в кавычки строка, реализующая λ-выражение, является референтом концепта), и двух отношений – «Def» и «GT». Таким образом, в тексте приведена часть описания иерархии типов концептов, которая структурно представляет собой обычный КГ. Отличие состоит лишь в назначении этого графа, необходимого при интерпретации для выявления схемы типизации концептов, определяющей номенклатуру используемых типов, и отношения между отдельными типами.

После включения метки «Т» из примера 1 в соответствующую иерархию типов концептов идентификатор «T» становится в пределах описываемого КГ равноправным названием типа и может использоваться при описании произвольных концептов (например, концепт [T: Ivanov] будет обозначать человека с фамилией Иванов, проживающего в Москве).

Полностью аналогично в CGIF строятся определения типов отношений, которые также образуют соответствующую иерархию. Рассмотрим данную ситуацию на примере, в котором используем альтернативную форму записи λ-выражений.

Пример 2. Пусть в CGIF-тексте присутствует фрагмент:

[LambdaExpression *w]

( (lambda (Person*x, City*y) [Go *z] (Agnt ?z ?x) (Dest ?z ?y)) ?w)

[RelationLabel: GoingTo *v]

(Def [?v] [?w])

Приведенный текст описывает новый тип отношений с меткой «GoingTo» (такие метки имеют предопределенный тип «RelationLabel») на основе λ-выражения, задающего уже рассматривавшуюся в 1.2 обобщенную ситуацию «Некоторый человек направляется в некоторый город». В отличие от примера 1 в данном случае λ-выражение не помещается в концепт с предопределенным типом «LambdaExpression» в виде ограниченной кавычками строки, а реализуется в отдельном отношении, содержащем запись самого выражения («(lambda …)») и связанную метку «?w», указывающую на концепт типа «LambdaExpression» (если в записи концепта отсутствует референт, то двоеточие после метки типа концепта опускается). После введения типа «GoingTo» в описании КГ может быть использована, например, следующая конструкция:

( GoingTo [Person: Ivanov] [City:Moscow] ),

которая будет обозначать ситуацию «Иванов направляется в Москву». При интерпретации приведенная запись будет развернута в полное описание вида:

[Go *x] (Agnt ?x [Person: Ivanov]) (Dest ?x [City: Moscow]).

Помимо λ-выражений в CGIF поддерживается и расширенный синтаксис описания новых типов концептов и отношений. Здесь могут использоваться отрицания («~»), конъюнкции («&») и дизъюнкции (« | ») меток типов (или выражений, описывающих эти метки), реализуемые в форме отношения. Например, конструкция «[( A & B & C ): D]» будет обозначать, что референт D одновременно относится к типам A, B и C, а «[~A : D]» будет определять тип концепта с референтом D как «любой тип, кроме A». Таким образом, принадлежность к тому или иному типу может задаваться произвольной логической формулой, использующей скобочные конструкции и операции «И», «ИЛИ» и «НЕ» над метками типов. Допускается также введение типов с применением базовых структур CGIF – множеств и последовательностей, которые будут рассматриваться в 1.3.