1. Лабораторна робота №1 Визначення механічних характеристик бетону

1.1. Мета роботи: Дослідним шляхом визначити кубикову і призмову міцність та пружно-пластичні характеристики бетону

1.2. Конструкція зразків та схема випробування. Кубикова міцність бетону визначається шляхом випробування кубиків з розміром ребра 15 см. Випробування трьох кубиків виконуються в гідравлічному пресі за схемою, представленою на рис 1.1.

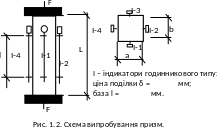
Призмова міцність визначається шляхом випробування на стиск призм розміром 10×10×40 см або 15×15×60 см. Навантаження здійснюється в гідравлічному пресі ступенями, величина яких повинна складати приблизно 10 % від руйнівного зусилля F_u. На кожному ступені навантаження вимірюються деформації за допомогою індикаторів годинникового типу, які кріпляться до призм з чотирьох сторін за допомогою спеціальних держаків (рис. 1.2).

1.3. Визначення кубикової міцності і класу бетону. Результати випробувань кубів заносяться в табл. 1.1. Міцність окремих зразків визначається за формулою

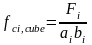(МПа). (1.1)

Таблиця 1.1

Результати випробування кубів

Марка зразків	Розміри a×b, см	Руйнуюче зусилля F, кН	Кубикова міцність, МПА		Статистики
			зразків fci,cube	сeредня fcm,cube	середнє квадратичне відхилення σ, МПа	Коефіцієнт мінливості υ, %
К-1
К-2
К-3

Середня кубикова міцність бетону буде дорівнювати

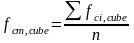(МПа), (1.2)

де n – кількість випробуваних зразків.

Середнє квадратичне відхилення

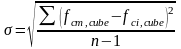. (1.3)

Коефіцієнт мінливості міцності визначається за формулою

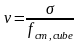. (1.4)

(нормоване значення ν = 0,135).

Клас бетону можна визначити за формулою

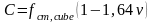. (1.6)

Отримане значення округлюється до меншого значення, передбаченого в нормах [3].

Відносні деформації призми на ступенях навантаження визначаються за формулою і заносяться в табл. 1.2

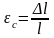, (1.7)

де Δl – середня абсолютна деформація при заданому F, мм;

l – база приладів, мм.

Дослідне значення призмової міцності бетону

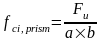. (1.8)

Теоретичне значення призмової міцності за формулою О.О. Гвоздєва

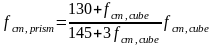, (1.9)

де f_cm,cube – середня кубикова міцність бетону.

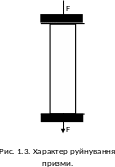
1.4. Визначення призмової міцності бетону. Результати випробовування призм заносяться в табл. 1.2. За схемою на рис. 1.3 відображається характер руйнування призми (розташування тріщин перед руйнуванням).

Відповідно до визначеного класу бетону знаходиться за [3] середнє значення призової міцності бетону і порівнюється з дослідним.

1.5. Визначення пружно-пластичних характеристик бетону. Обробку отриманих результатів виконують у табличній формі (табл. 1.3). На підставі статистичної обробки в Excel залежності «E_c – η» отримаємо рівняння (лінія тренда) у вигляді

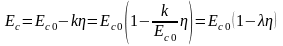, (1.10)

де λ – коефіцієнт пластичності бетону;

ν = 1 – λ – коефіцієнт пружності бетону.

Таблиця 1.2

Результати випробування призми

Номер ступені навантаження	Навантаження, F, кН	Відліки по приладам				Абсолютна деформація призми Δli, мм				Середня абсолютна деформація Δl, мм	Відносна деформація εс*105
		I-1	I-2	I-3	I-4	I-1	I-2	I-3	I-4
0
1
2
3
4
5
6
7
8
9
10

Відносна деформація . Розміри поперечного перерізу a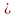 b = см. Руйнуюче зусилля F_u = кН.

Таблиця 1.3

Обробка результатів випробовування призми

Номер ступені навантаження	Зусилля F, кН	Напруження σс, МПа	Рівень навантаження	Відносна деформація εс×105	Модуль пружно пластичності Eс×10-4, МПа
0
1
2
3
4
5
6
7
8
9
10

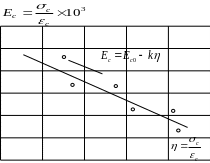
Рис.1.5. Залежність модуля пружно-пластичності 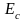від

рівня навантаження .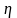

За даними табл. 1.3 будуються залежності «σ_с – ε_с» та «E_c – η» (рис. 1.4 і рис. 1.5).

Модуль пружності бетону E_с0 визначається за формулою (1.10) при σ_с = 0 (η = 0), а початковий E_с – при η = 0,3