Контрольна робота з теорії ймовірності.
Варіант №1.
№1. Два стрільці, для яких ймовірності влучення в мішень дорівнює відповідно 0,7 і 0,8, роблять по одному пострілу. Знайти ймовірність того, що: а) обидва стрільці влучать в мішень; б) жодний із стрільців не влучить в мішень ; в) хоча б один із стрільців влучив в мішень; г) лише один із стрільців влучить в мішень.
№2. У трьох урнах лежать білі і чорні кулі .У першій урні лежить 3 білі і 1 чорна , у другій -6 білих і 4 чорних , у третій - 9 білих і 1 чорна .З навмання взятої урни виймають одну кулю. Знайти ймовірність того, що вона біла.
№3. Схожість насіння певного сорту рослини оцінюється ймовірністю р.
Знайти ймовірність того, що : а) з n1 насінин зійде k1;
б) з n2 насінин зійде k2;
в) з n2 насінин зійде від k2 до k3;
г) відносна частота насінин, які зійдуть, відхилиться по абсолютній величині від її ймовірності на величину, не більше за ε при n2.
р = 0,9; g=1-р=0,1; n1=8; n2 = 600; k1 = 6; k2 = 480; k3 = 560; ε = 0,02.
№4. Необхідно знайти:
а) математичне сподівання;
б) дисперсію;
в) середнє квадратичне відхилення дискретної випадкової величини Х з законом розподілу, який задано таблицею (в першому рядку стоять усі можливі значення випадкової величини Х, а в другому – ймовірності можливих значень).
Х |
15 |
19 |
24 |
29 |
30 |
р |
0,1 |
0,2 |
0,2 |
0,1 |
0,4 |
№5. Випадкова неперервна величина Х задана інтегральною функцією розподілу F(х). Знайти:
1) диференціальну функцію розподілу (щільність розподілу) f(х);
2) математичне сподівання М[х];
3) дисперсію D[х].
Побудувати графіки функції розподілу та щільності розподілу.
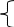
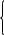0 при х ≤
0
F(х) = х2/4 при 0 < х ≤ 2
1 при х > 2
Контрольна робота.
Варіант №2.
№1. У кожному з трьох ящиків лежить по 10 деталей, у першому ящику 2 браковані, у другому – 3, у третьому - 1. З кожного ящика беруть по одній деталі. Знайти ймовірність того ,що: а) всі 3 деталі браковані; б) всі 3 деталі стандартні; в) серед трьох деталей є одна стандартна.
№2. Відомо, що 5% чоловіків і 0,25% жінок – дальтоніки. Навмання обрана особа – дальтонік. Яка ймовірність того, що це чоловік. (Вважати що чоловіків і жінок однакова кількість.).
№3. Схожість насіння певного сорту рослини оцінюється ймовірністю р.
Знайти ймовірність того, що : а) з n1 насінин зійде k1;
б) з n2 насінин зійде k2;
в) з n2 насінин зійде від k2 до k3;
г) відносна частота насінин, які зійдуть, відхилиться по абсолютній величині від її ймовірності на величину, не більше за ε при n2.
р = 0,8; g=1-р=0,2; n1=8; n2 = 100; k1 = 7; k2 = 80; k3 = 90; ε = 0,01.
№4. Необхідно знайти:
а) математичне сподівання;
б) дисперсію;
в) середнє квадратичне відхилення дискретної випадкової величини Х з законом розподілу, який задано таблицею (в першому рядку стоять усі можливі значення випадкової величини Х, а в другому – ймовірності можливих значень).
Х |
8 |
12 |
18 |
24 |
30 |
р |
0,3 |
0,1 |
0,3 |
0,2 |
0,1 |
№5. Випадкова неперервна величина Х задана інтегральною функцією розподілу F(х). Знайти: