3.2 Вывод операторного выражения входной функции

K(P)=1, т.к. нагрузка является двухполюсником

Методом последовательного преобразования схемы нагрузки выведем операторную функцию цепи. Учитывая, что и получим:

, где

Проверка на размерность:

PL имеет размерность [Ом], а PC имеет размерность[Ом^-1]

Проверка на крайних частотах:

при p=0

при p=∞ входное сопротивление равно отношению коэффициентов при старших степенях Z(∞)=R.

Проверка максимального порядка полиномов:

; m=2; n=2;

, так как в схеме 2 реактивности и нет ни емкостных контуров, ни индуктивных сечений даже при подключении источников напряжения или тока.

3.3 Нормировка операторной функции

Подставив нормированные значения в операторную функцию C­=1; L=1; Rш=10; R=0,1; получим:

В выражение Z(p) вместо р подставляем j*w. Построим графики АЧХ И ФЧХ входной функции Mathсad.

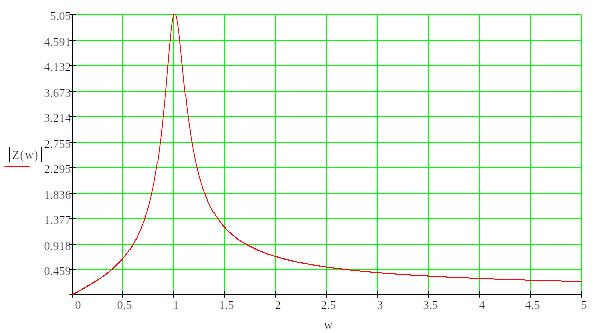
Рисунок 3.5 АЧХ входной функции

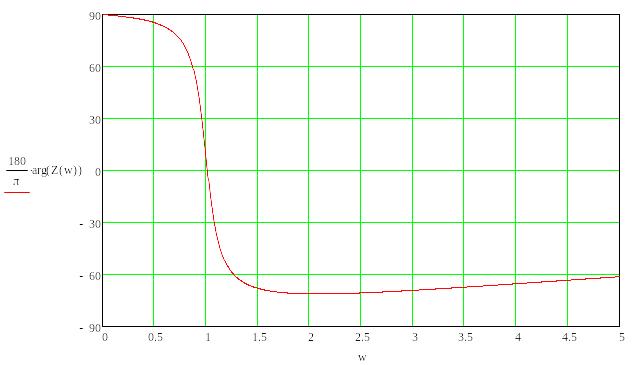
Рисунок 3.6 ФЧХ входной функции

3.4 Расчет резонансных частот и резонансных сопротивлений. Определение ппц

Определение резонансной частоты и резонансного сопротивления проводится на основе нормированного выражения (значок «н» опущен) для нагрузки. В соответствии с определением фазового резонанса на частоте входное сопротивление чисто активно и равно :

,

,

Перейдём к ненормированным значениям:

Ом Ом

рад/с рад/с

Гц МГц

2) Расчет полосы пропускания цепи (ППЦ):

Для определения полосы пропускания цепи найдем максимальное значение нормированной функции входа:

Приравняем входную функцию к и решим уравнение:

Решая уравнение получим:

; .

Откуда видно что полоса пропускания цепи равна:

4. Исследование модели транзистора с обобщенной нагрузкой

4.1 Нахождение операторных выражений для Zт(p) и Кт(р)

Для реализации МУП на вход подключим пробный источник , обозначим узлы, элементы схемы опишем проводимостями в операторной форме и учтём, что теперь , а что и представлено на рисунке 4.1

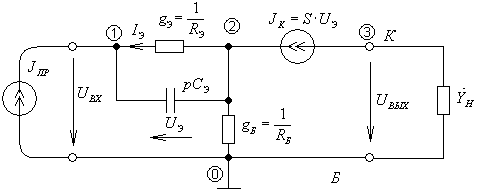
Рисунок 4.1 – Модель транзистора с обобщённой нагрузкой

Входная функция: Передаточная функция:

;

Запишем типовую систему для данной модели схемы:

.

Выразим зависимый источник тока через узловые потенциалы:

.

Подставим полученное выражение в систему и приведём подобные по узловым потенциалам.

.

Запишем полученную систему в матричной форме.

По правилу Крамера найдём узловые потенциалы и ,

;

;

, где определитель матрицы проводимостей.

;

;

.

Схемную функцию входного сопротивления и передаточной функции найдём как

;

.

Таким образом:

;

.

Проверка полученных выражений

Проверяем полученные выражения схемных функций по размерности:

При проверке учитываем, что произведение имеет размерность , а произведение и R - размерность .

Проверка по размерности подтвердила правильность нахождения схемных функций.

Проверка на крайних частотах диапазона:

Эквивалентные модели транзистора с обобщённой нагрузкой для крайних частот диапазона представлены на рисунке 4.2.

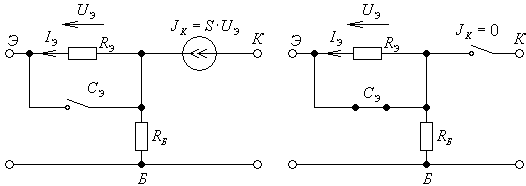
Рисунок 4.2 – Эквивалентные модели схемы на частотах и

При и если учесть, что , то выражение для передаточной функции примет вид:

, отсутствие отрицательного знака говорит об отсутствии инверсии в схеме с ОБ

Для входной функции при :

,

Т.к.

При , так как .

, что совпадает со схемой (закоротко на С_Э).

Из рисунка 3.2 видно, что (закоротко на С_Э). При .

В итоге получили, что полученные выражения схемных функций соответствуют моделям на крайних частотах.

Проверка на соответствие степеней полиномов порядку цепи:

Определение максимального порядка полиномов функции непосредственно по схеме осуществляется по следующему правилу:

где n, m – максимальные степени полиномов числителя и знаменателя соответственно;

– число независимых реактивностей;

– число ёмкостных контуров;

– число индуктивных сечений.

Для определения порядка числителя на вход схемы подключается источник э.д.с., а знаменателя – источник тока.

Из схемы цепи видно, что число независимых реактивностей равно 1 и в схеме отсутствуют ёмкостные контура и индуктивные сечения, поэтому максимальные степени числителя и знаменателя определятся из соотношения

Числитель функции и знаменатель функции и совпадают с точностью до общего множителя, так как при определении обеих функций входные зажимы одни и те же:

Проведенная проверка показала, что схемные функции транзистора найдены верно.