3. Решение задач

Задача 3.1. Найдите , если А={1; 2}, В={1; 2; 3}.

Решение: ={(1;1), (1;2), (1;3), (2;1), (2;2), (2;3)}. Ответ: ={(1;1), (1;2), (1;3), (2;1), (2;2), (2;3)}.

Задача 3.2. Найдите , если .

Решение: . Ответ: А²={(1;1); (1;2); (2;1); (2;2)}

Задача 3.3. Изобразите на декартовой плоскости множество . Решение.

y

Каждый элемент множества представляет собой упорядоченную пару , где , , 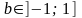изображаемую на декартовой плоскости точкой . Значит множество на декартовой плоскости представляет собой множество точек, первая координата которых берется из , а вторая – из . (Рисунок 1).

2

1

х

1

2

0

-1

-2

-2

Рисунок 1 – Решение задачи 3.3.

Задача 3.4. Изобразите на координатной плоскости декартово произведение А×В, если: А= {1,2,3} ,В=[3,5]; Решение:

y

Так как множество А состоит из трёх элементов, а множество В содержит все действительные числа от 3 до 5, включая и сами эти числа, то декартово произведение А х В будет состоять из бесконечного множества пар, первая компонента которых либо 1, либо 2, либо З, а вторая - любое действительное число из промежутка [3, 5]. Такое множество пар действительных чисел на координатной плоскости изобразится тремя отрезками (Рисунок 2).

5

3

x

1

2

3

Рисунок 2 – Решение задачи 3.4.

у

Задача 3.5. Изобразите на координатной плоскости декартово произведение А×В, если: А=[1,3], В=[3,5]; Решение:

В этом примере бесконечны оба множества А и В. Поэтому первой координатой пары, принадлежащей множеству А х В, может быть любое число из промежутка [1, 3], и, следовательно, точки, изображающие элементы декартова произведения данных множеств А и В, образуют квадрат. Чтобы подчеркнуть, что элементы декартова произведения изображаются и точками, лежащими внутри квадрата, этот квадрат можно заштриховать (Рисунок 3).

5

3

х

3

1

Рисунок 3 – Решение задачи 3.5.

Задача 3.6. Даны множества А={1,2,5}, B={4,6}, C={7,8}. Найти декартово произведение множества A x B x C. Решение: A x B x C={(1,4,7); (1,4,8); (1,6,7); (1,6,8); (2,4,7); (2,4,8); (2,6,7); (2,6,8); (5,4,7); (5,4,8); (5,6,7); (5,6,8)} Ответ: A x B x C={(1,4,7); (1,4,8); (1,6,7); (1,6,8); (2,4,7); (2,4,8); (2,6,7); (2,6,8); (5,4,7); (5,4,8); (5,6,7); (5,6,8)}

Задача 3.7. Пусть А={1, 2, 3} и В={а, b}. Найти декартовы произведения А х В и В х А. Найти мощности этих декартовых произведений. Решение: По определению декартового произведения: A x B={(1, a); (1, b); (2, a); (2, b); (3, a); (3, b)} B х A={(a, 1); (a, 2); (a, 3); (b, 1); (b, 2); (b, 3)} Очевидно, что A x B= B х A. Мощности полученных декартовых произведений равны: |A x B|= |B х A|=|A||B|=3*2=6 Ответ: Мощности декартовых произведений равны 6.

Задача 3.8. Докажите, что при любых множествах , , .

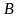Решение: Обозначим , 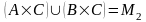. Следовательно нам надо доказать, что .

1)

2)

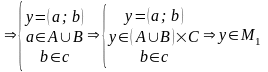
Задача 3.9. Докажите теорему, что для конечных множеств А и В |A x B| =|A| |B|.

Доказательство. Первый компонент упорядоченной пары можно выбрать |A| способами, второй - |B| способами, причем независимо от выбора первого элемента. Таким образом, всего имеется |A| |B| различных упорядоченных пар.

ЛЕММА (A x B) x C ~ A x (B x C)

Доказательство

(A x B) x C = {((a, b) c} | (a, b) ϵ А x B & c ϵ C} = {((a, b)c} |a ϵ A & b ϵ B & c ϵ C} ^{(a, b, c)→(a, (b, c))} ~ {(a, (b, c)) | a ϵ A & (b, c) ϵ B x C} = A x (B x C). Теорема доказана.

Задача 3.10. Докажите свойство A x (B  C) = (A x B)  (A x C). Это свойство будем доказывать методом двух включений.

Доказательство

Если (x, y) ϵ A x (B  C), то x ϵ А и y ϵ B  C. Из того, что y ϵ B  C, следует y ϵ B или y ϵ С. Если y ϵ B, то (x, y) ϵ A x B, а если y ϵ С, то (x, y) ϵ A x С. Итак (x, y) ϵ A x B или (x, y) ϵ A x С, то есть (x, y) ϵ (A x B)  (A x C). Следовательно, A x (B  C) (A x B)  (A x C). Свойство доказано.