2. Определение расчетного расхода

Статистическая обработка полученного ряда наибольших годовых расходов ведется также в табличной форме (табл.2).Выписанный в хронологическом порядке ряд расходов упорядочивается (ранжируется) по величине от максимального к минимальному (графа 5). Обрабатываемый ряд должен быть непрерывным, поэтому отдельного стоящий большой расход 1924 г. в табл.5 не включается. Подсчитываем сумму расходов, средний расход, эмпирическая вероятность превышения каждого из наблюдаемых расходов:

,

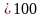где m-номер расхода в ранжированном ряду;

n=14-количество членов ряда.

Мерой изменчивости ряда в гидрологических расчётах служит коэффициент вариации:

,

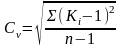где К_i=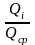 - модульный коэффициент.

При включении в обрабатываемый ряд редкого расхода, надежность расхода существенно повышается. Объем удлиненного ряда:

N=1977-1924+1=54

Табл. 2 Обработка результатов наблюдений

Год	Q,М³/сек	№ члена ряда	Ранжированный ряд			Pэ,%		Ki		Кi-1			(Ki -1)²
			год	Qi	+					-
1964	599	1	1974	2722	4,9		3,647		2,39			5,734
1965	422	2	1967	1765	11,8		2,621		1,20			1,443
1966	337	3	1975	1379	18,8		1,525		0,72			0,518
1967	1765	4	1969	723	25,7		0,973				0,10	0,010
1968	331	5	1977	711	32,6		0,818				0,11	0,013
1969	723	6	1964	599	39,6		0,653				0,25	0,064
1970	485	7	1972	514	46,5		0,580				0,36	0,129
1971	407	8	1970	485	53,5		0,560				0,40	0,156
1972	514	9	1973	462	60,4		0,557				0,42	0,180
1973	462	10	1965	422	67,4		0,515				0,47	0,224
1974	2722	11	1971	407	74,3		0,463				0,49	0,242
1975	1379	12	1976	369	81,3		0,427				0,54	0,291
1976	369	13	1966	337	88,2		0,364				0,58	0,336
1977	711	14	1968	331	95,1		0,298				0,59	0,345
				∑Q1	11226		14					9,6854
				Qср	802

Средний расход:

Q_{ср= )}

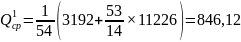
Коэффициент вариации:

=

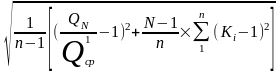
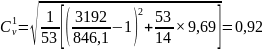
Удлинение ряда расходов меняет порядковые номера членов ряда. На первое место ставится максимальный расход (паводок 1924 года), следовательно, остальные номера увеличиваются на единицу. Кроме того, ряд как бы растягивается с 14 до 54 лет и порядковые номера его членов увеличиваются пропорционально этому удлинению:

;

Соответственно меняется эмпирическая вероятность превышения:

;

Значение модульных коэффициентов при удлинений ряда несколько уменьшается (табл.3).

Табл. 3 Значения коэффициентов

М1	1,0	7,2	10,8	14,4	18,0	21,6	25,2	28,8
Р! э	1,29	13,23	19,85	26,47	33,09	39,70	46,32	52,94
К!I	3,77	3,21	2,09	1,63	0,85	0,84	0,7	0,61

Зависимость модульных коэффициентов от их вероятности строят клетчатки вероятностей. Используя теоретические кривые, строящиеся по таблицам С.Н.Крицкого и М.Ф.Менкаля, составляем табл.4 и затем наносим на клетчатку вероятностей.

Табл. 4 Данные для клетчатки вероятностей

Р,%				0,10		0,33		0,50		1,0		2,0		5,0		10,0		20,0		25,0		30,0		40,0		50,0
Сν= 0,92	Кi	CsСv	1		4,19		3,86		3,74		3,52		3,24		2,82		2,39		1,8		1,59		1,40		1,04		-
			1,5		5,33		4,62		4,41		3,99		3,49		2,85		2,3		1,68		1,47		1,30		0,99		0,75
			2		6,25		5,18		4,84		4,24		3,59		2,82		2,21		1,59		1,38		1,22		0,95		0,74
			3		7,55		5,83		5,34		4,5		3,71		2,74		2,1		1,47		1,28		1,14		0,9		0,73
		КрВП-65			5,57		4,89		4,66		4,24		3,61		2,82		2,21		1,59		-		-		-		0,74

Рис. 3 Клетчатка вероятностей

Кривая = 1,5 наиболее подходящая закономерность распределения расходов, при вероятности Р=1% имеет модульный коэффициент К₁(%)=3,99

Отсюда расход расчетного паводка Q_РАСЧ.=Q_СР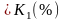

Q_РАСЧ.=802*3,99=

3200

м³/с

Уровень воды при расчетном расходе определяется экстраполяцией зависимости уровня от расхода, рис 2.

Следует иметь в виду, что экстраполяция эмпирических зависимостей может дать существенную погрешность. Поэтому полученный уровень – расчетный горизонт воды (РГВ) нуждается в проверке (табл. 5).

Табл. 5 Проверка расчетного горизонта

Н	-	1,77		2,67		3,97		8,47		7,07		4,97		3,57			3,12		0,72		-	Расчетный паводок 108,47 Qрасч= 3200
НСР	0,885		2,22		3,32		6,22		7,77		6,02		4,27			3,345		1,92		0,36
W	17,7		88,8		33,2		373,2		621,6		301		896,7			836,25		345,6		19,98
VСР	0,26		0,40		0,54		1,61		1,81		1,58		0,53			0,43		0,31		0,09
Q	4,34		35,5		17,37		600,32		1126,58		476,36		472,56			360,46		105,47		1,79
	Qлп=57							Qрусла=2203							Qпп=940