Вопросы для самопроверки

1. Расскажите о лесных богатствах нашей страны. 2. Какие породы и лесо­материалы применяются в деревянных конструкциях и как они сортируются по качеству? 3. В чем преимущества древесины как конструкционного строитель­ного материала? 4. Каково строение древесины? Что такое пороки и анизотропия древесины и как они влияют на ее прочность? 5. Каковы собственная масса, прочность и жесткость древесины и как на них влияет влажность? 6. При каких условиях древесина гниет и методы защиты ее от гниения? 7. При каких условиях древесина горит и методы защиты ее от горения? 8. Что такое строи­тельная фанера и каковы ее строение и достоинства как конструкционного материала? 9. Какие конструкционные пластмассы применяются для строитель­ных конструкций и каковы их общие достоинства и недостатки? 10. Что такое стеклопластики, их строение, прочность и применение? И. Что такое пенопласты, какова их структура, плотность и применение? 12. Что такое оргстекло, его основное достоинство и применение? 13. Что такое воздухонепроницаемые ткани, каково их строение и где они применяются? 14. Что такое винипласт, каково его основное достоинство и где он применяется? 15. Что такое древесные пласти­ки, их строение, свойства и применение? 16. Какие неорганические конструкцион­ные материалы применяются в конструкциях из дерева и пластмасс?

СРС №12: «Расчет элементов деревянных конструкций»

1. Особенности расчета по предельным состояниям

В конструк­циях из дерева и пластмасс также как и в конструкциях из других материалов могут возникать две группы предель­ных состояний — первая и вторая.

Первая группа наиболее опасна. Она определяется непригод­ностью к эксплуатации, когда конструкция теряет несущую спо­собность в результате разрушения или потери устойчивости. Это­го не происходит, пока нормальные максимальные или скалы­вающие напряжения в ее элементах не превосходят расчетных (минимальных) сопротивлений материалов, из которых они изго­товлены. Это условие записывается формулой

(1)

Вторая группа менее опасна. Она определяется непригод­ностью конструкции к нормальной эксплуатации, когда она про­гибается до недопустимой величины. Этого не происходит, пока максимальный относительный прогиб ее не превосходит пре­дельно допускаемых значений. Это условие записывается фор­мулой

(2)

Целью расчета является не допустить ни первого, ни второго предельного состояний в процессах перевозки, сборки и эксплуа­тации конструкции. Это выполняется на основании учета норма­тивных и расчетных нагрузок и сопротивлений материалов.

Нагрузки, действующие на конструкции, определяются Строи­тельными нормами и правилами — СНиП 2.01.07—85 «Нагрузки и воздействия». При расчете конструкций из дерева и пластмасс учитываются, главным образом, постоянная нагрузка от собст­венного веса конструкций и других элементов зданий g и кратко­временные нагрузки от веса снега S, давления и отсоса ветра W. Учитываются также нагрузки от веса людей и оборудования. Каждая нагрузка имеет нормативное и расчетное значение. Нор­мативное значение удобно обозначать индексом .

Нормативные нагрузки являются исходными зна­чениями нагрузок. Временные нагрузки определяются в резуль­тате обработки данных многолетних наблюдений и измерений. Постоянные нагрузки вычисляются по значениям собственного веса и объема конструкций, прочих элементов здания и обору­дования. Нормативные нагрузки учитываются при расчете кон­струкций по второй группе предельных состояний — по прогибам.

Расчетные нагрузки определяются на основании нормативных с учетом их возможной переменчивости, особенно в большую сторону. Для этого значения нормативных нагрузок умножают на коэффициент надежности по нагрузке , значения которого различны для разных нагрузок, но все они больше единицы. Значения распределенных нагрузок даются в нормах в килопаскалях (кПа), что соответствует килоньютонам на квадратный метр (кН/м). В большинстве расчетов применяются линейные значения нагрузок (кН/м). Расчетные нагрузки применяются при расчете конструкций по первой группе предельных состоя­ний, по прочности и устойчивости.

Постоянная нормативная нагрузка «g», действующая на кон­струкцию, состоит из двух частей: первая часть — нагрузка от всех элементов ограждающих конструкций и материалов, поддерживаемых данной конструкцией. Нагрузка от каждого эле­мента определяется путем умножения его объема на плотность материала и на шаг расстановки конструкций; вторая часть - нагрузка от собственного веса основной несущей конструкции. При предварительном расчете нагрузку от собственного веса основной несущей конструкции можно определить приближенно, задаваясь реальными размерами сечений и объемами элементов конструкции. Для этого можно также воспользоваться эмпири­ческой формулой

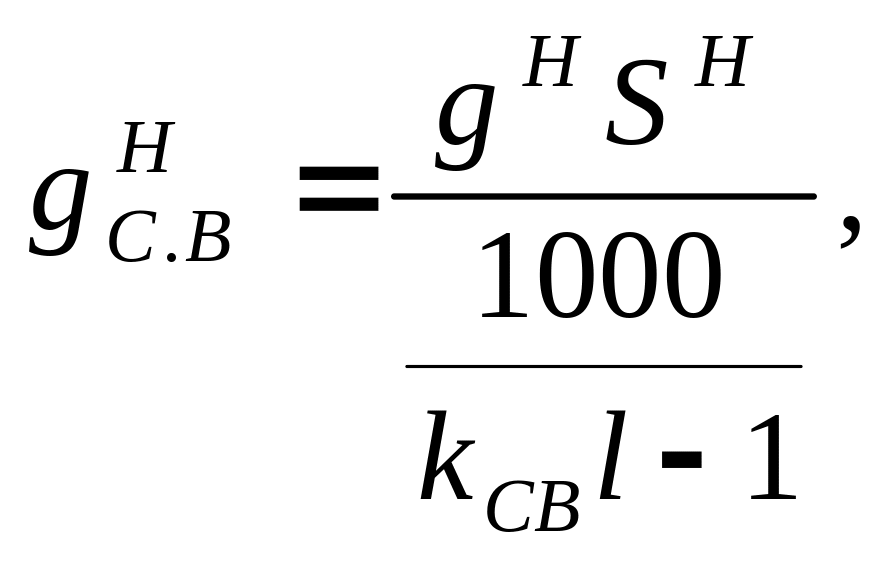
где -- постоянная нагрузка от веса поддерживаемых элемен­тов; — временная снеговая нагрузка; — коэффициент соб­ственного веса.

В состав этой формулы включаются и другие значительные постоянные нагрузки.

Постоянная расчетная нагрузка g равна произведению нор­мативной на коэффициент надежности по нагрузке . Для наг­рузки от собственного веса конструкций = 1,1, а для нагрузок от утепления, кровли, пароизоляции и других = 1,3. Постоян­ную нагрузку от обычных скатных покрытий с углом наклона удобно относить к их горизонтальной проекции путем деления ее на .

Нормативная снеговая нагрузка определяется исходя из нормативного веса снегового покрова , который дается в нор­мах нагрузок (кН/м²) горизонтальной проекции покрытия в за­висимости от снегового района страны. Эту величину умножают на коэффициент , учитывающий уклон и другие особенности формы покрытия. Тогда нормативная нагрузка . При двускатных покрытиях, имеющих 25°, = 1, при а ^ 60° = 0, а при промежуточных углах наклона 60° > > 25° = (60° — °)/35°. Эта нагрузка является равномерной и мо­жет быть дву- или односторонней.

При сводчатых покрытиях по сегментным фермам или аркам равномерная снеговая нагрузка определяется с учетом коэффи­циента , который зависит от отношения длины пролета к вы­соте свода .

При отношении высоты свода к пролету 1/8 снеговая нагрузка может быть треугольной с максимальным значением на одной опоре и 0,5 на другой и нулевым значением в коньке. Коэффициенты , определяющие величины максимальной снеговой нагрузки при отношениях = 1/8, 1/6 и 1/5, соответ­ственно равны 1,8; 2,0 и 2,2.

Снеговая нагрузка на покрытия стрельчатой формы может определяться как на двускатные, считая условно покрытие дву­скатным по плоскостям, проходящим через хорды осей полуарок.

Расчетная снеговая нагрузка равна произведению норматив­ной нагрузки на коэффициент надежности по нагрузке Для большинства легких деревянных и пластмассовых конструкций при отношении нормативных постоянной и снеговой нагрузок < 0,8 коэффициент = 1,6. При больших отношениях этих нагрузок = 1,4.

Нагрузка от веса человека с грузом принимается равной - нормативная = 0,1 кН и расчетная = = 0,1 • 1,2 = 1,2 кН.

Ветровая нагрузка. Нормативная ветровая нагрузка w состоит из давления и отсоса ветра. Исходными дан­ными при определении ветровой нагрузки являются значения давления ветра, направленного перпендикулярно поверхностям покрытия и стен зданий (МПа), зависящие от ветрового райо­на страны и принимаемые по нормам нагрузок и воздействий. Нормативные ветровые нагрузки определяются умножением нормального давления ветра на коэффициент k, учитывающий высоту зданий, и аэродинамический коэффициент , учитываю­щий его форму. Для большинства зданий из дерева и пласт­масс, высота которых не превышает 10 м, k = 1. Таким образом, нормативная ветровая нагрузка на такие здания .

Аэродинамический коэффициент зависит от формы здания, его абсолютных и относительных размеров, уклонов, относитель­ных высот покрытий и направления ветра. На большинство скат­ных покрытий, угол наклона которых не превышает = 14°, ветровая нагрузка действует в виде отсоса . При этом она в основном не увеличивает, а уменьшает усилия в конструкциях от постоянных и снеговых нагрузок и при расчете может не учитываться в запас прочности. Ветровая нагрузка должна обя­зательно учитываться при расчете стоек и стен зданий, а также при расчете конструкций треугольной и стрельчатой формы.

Расчетная ветровая нагрузка равна нормативной, умножен­ной на коэффициент надежности = 1,4. Таким образом

Нормативные сопротивления древесины (МПа) являются основными характеристиками прочности древесины чистых от пороков участков. Они определяются по результатам многочис­ленных лабораторных кратковременных испытаний малых стан­дартных образцов сухой древесины влажностью 12 % на растяжение, сжатие, изгиб, смятие и скалывание. Например, образец на сжатие имеет сечение 2 X 2 см и длину 3 см. Результаты этих испытаний имеют большой разброс. Они обрабатываются статистически, и с учетом коэффициента изменчивости ст норма­тивное сопротивление вычисляется по формуле

(3)

Например, при сжатии = 33(1 —2,25*0,105) = 25 МПа. Сле­довательно, 95 % испытанных образцов древесины будут при сжатии иметь прочность , равную или большую, чем ее нор­мативное значение.

Значения нормативных сопротивлений практически используются при лабораторном контроле прочности древесины в процессе изготовления деревянных конструкций и при определении несущей способности эксплуатируемых несущих конструкций при их обследованиях.

Расчетные сопротивления древесины R (МПа) — это основ­ные характеристики прочности реальной древесины элементов реальных конструкций. Эта древесина имеет естественные допус­каемые пороки и работает под нагрузками в течение многих лет. Расчетные сопротивления получаются на основании норма­тивных сопротивлений с учетом коэффициента надежности по материалу и коэффициента длительности нагружения по формуле

Коэффициент значительно больше единицы. Он учитывает снижение прочности реальной древесины в результате неодно­родности строения и наличия различных пороков, которых не бывает в лабораторных образцах. В основном прочность дре­весины снижают сучки. Они уменьшают рабочую площадь се­чения, перерезая и раздвигая ее продольные волокна, создают эксцентриситет продольных сил и наклон волокон вокруг сучка. Наклон волокон вызывает растяжение древесины поперек и под углом к волокнам, прочность которой в этих направлениях зна­чительно ниже, чем вдоль волокон. Пороки древесины почти в два раза снижают прочность древесины при растяжении и при­мерно в полтора раза при сжатии. Трещины наиболее опасны в зонах работы древесины на скалывание. С увеличением разме­ров сечений элементов напряжения при их разрушении умень­шаются за счет большей неоднородности распределения напря­жений по сечениям, что тоже учитывается при определении рас­четных сопротивлений.

Коэффициент длительности нагружения . Он учиты­вает, что древесина без пороков может неограниченно долго выдерживать лишь около половины той нагрузки, которую она выдерживает при кратковременном нагружении в процессе испытаний. Следовательно, ее дли­тельное сопротивление поч­ти вдвое ниже кратковремен­ного.

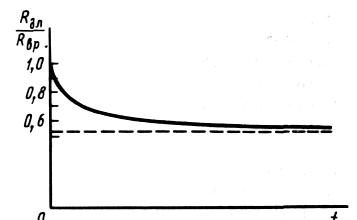
Это иллюстрируется кривой длительного сопротивления, по­лученной в результате много­летних испытаний (рис. 1). Она показывает, что отноше­ние , вначале равное единице, уменьшается по мере увеличения длительности дей­ствия нагрузки до того време­ни, когда это отношение становится постоянным. Эта величина и называется пределом дли­тельного сопротивления древесины. Для реальной древесины с допускаемыми пороками величина предела длительного сопро­тивления с учетом того, что временные нагрузки действуют не постоянно и длительное сопротивление древесины несколько вы­ше, достигает 0,66. При этом затухает и деформация ползуче­сти, которая была максимальной в начале нагружения.

Рис. 1. Характеристики прочности древесины вдоль волокон

Качество древесины естественно влияет на величины ее рас­четных сопротивлений. Древесина 1-го сорта — с наименьшими пороками имеет наибольшие расчетные сопротивления. Расчет­ные сопротивления древесины 2-го и 3-го сортов соответственно ниже. Например, расчетное сопротивление древесины сосны и ели 2-го сорта сжатию получается из выражения

= 25*0,66/1,25 = 13 МПа.

Расчетные сопротивления древесины сосны и ели сжатию, растяжению, изгибу, скалыванию и смятию приведены в СНиП II.25-80.

Коэффициенты условий работы к расчетным сопротивле­ниям древесины учитывают условия, в которых изготовляются и работают деревянные конструкции. Коэффициент породы учитывает различную прочность древесины разных пород, отли­чающихся от прочности древесины сосны и ели. Коэффициент нагрузки учитывает кратковременность действия ветровой и монтажных нагрузок. При смятии = 1,4, при остальных видах напряжений = 1,2. Коэффициент высоты сечений при изгибе древесины клеедеревянных балок с высотой сечения более 50 см снижается от 1 до 0,8, при высоте сечения 120 см - еще более. Коэффициент толщины слоев клеедеревянных элемен­тов учитывает повышение их прочности при сжатии и изгибе по мере уменьшения толщины склеиваемых досок, в результате чего увеличивается однородность строения клееной древесины. Значения его

находятся в пределах 0,95...1,1. Коэффициент гнутья учитывает дополнительные напряжения изгиба, возни­кающие при выгибе досок в процессе изготовления гнутых клеедеревянных элементов. Он зависит от отношения радиуса выгиба к толщине досок и имеет значения 1,0...0,8 при увеличении этого отношения от 150 до 250. Коэффициент температуры учитывает снижение прочности древесины конструкций, работа­ющих при температуре от +35 до +50 °С. Он уменьшается от 1,0 до 0,8. Коэффициент влажности учитывает снижение прочности древесины конструкций, работающих во влажной сре­де. При влажности воздуха в помещениях от 75 до 95 % = 0,9. На открытом воздухе в сухой и нормальных зонах = 0,85. При постоянном увлажнении и в воде = 0,75. Коэффициент концентрации напряжения = 0,8 учитывает местное снижение прочности древесины в зонах врезками и отверстиями при растя­жении. Коэффициент длительности нагрузок = 0,8 учитывает снижение прочности древесины в результате того, что длитель­ные нагрузки составляют иногда более 80 % от общей суммы нагрузок, действующих на конструкцию.

Модуль упругости древесины, определенный при кратковременных лабораторных испытаниях, МПа. При учете деформаций при длительном нагружении, при расчете по прогибам МПа .

Нормативные и расчетные сопротивления строительной фане­ры были получены теми же способами, что и для древесины. При этом учитывалась ее листовая форма и нечетное число слоев с взаимно перпендикулярным направлением волокон. По­этому прочность фанеры по этим двум направлениям различна и вдоль наружных волокон она несколько выше.

Наиболее широко применяется в конструкциях семислойная фанера марки ФСФ. Ее расчетные сопротивления вдоль волокон наружных шпонов равны: растяжению = 14 МПа, сжатию = 12 МПа, изгибу из плоскости = 16 МПа, скалыванию в плоскости = 0,8 МПа и срезу = 6 МПа. Поперек волокон наружных шпонов эти величины соответственно равны: растяжению = 9 МПа, сжатию = 8,5 МПа, изгибу = 6,5 МПа, скалыванию = 0,8 МПа, срезу = = 6 МПа. Модули упругости и сдвига вдоль наружных волокон равны соответственно МПа и = 750 МПа и по­перек наружных волокон МПа и = 750 МПа.

Бакелизированная фанера имеет значительно более высокие расчетные сопротивления, достигающие при сжатии = 32 МПа. Расчетные сопротивления, модули упругости, сдвига и коэффициенты Пуассона , приведены в СНиП.

Нормативные и расчетные сопротивления конструкционных пластмасс определяются по той же методике, что и для древесины и фанеры, поскольку их проч­ности тоже имеют большой разброс и на них также оказывают значительное влияние длительность нагружения и условия рабо­ты. При этом необходимо учитывать особенности этих материа­лов. В них нет пороков, как в древесине, но есть дефекты изго­товления. Свойства их колеблются по толщине листов и особенно плит. Другие формы имеют лабораторные испытываемые образ­цы. Расчетные сопротивления конструкционных пластмасс, моду­ли их упругости, сдвига, коэффициенты Пуассона и линейного расширения приведены в СНиП. Коэффициенты условий ра­боты, учитывающие колебания влажности и температуры, при­ведены в СНиП.

Порядок расчета конструкций из дерева и пластмасс является таким же, как и для прочих конструкций и заключается в следующем. Определяют нормативные и расчетные нагрузки, линейно распределенные (кН/м) и сосредоточенные (кН). Затем методами строительной механики определяют опорные реак­ции — вертикальные R и горизонтальные Н; расчетные усилия - изгибающие моменты М, продольные N и поперечные Q силы.

Проверка напряжений нормальных и скалывающих про­изводится по формулам строительной механики. Изгибаемые элементы проверяются по прогибам от нормальных нагрузок.