Контрольные вопросы по теоретической механике (Динамика, II-ой коллоквиум)
Вопросы, перенесенные из I-ого коллоквиума:
4. Какие силы называются потенциальными? Приведите примеры потенциальных сил.
Это силы, зависящие от координат движущейся материальной точки. Эти силы так же называются позиционными. К числу таких сил относятся силы тяжести, упругости, тяготения.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Функция
зависит только от координат, и такая,
что частные производные от этой функции
по координатам равны проекциям силы
силового поля на соответствующие
координатные оси:
;
;
()
Функция , удовлетворяющая условиям (), называется силовой функцией данного силового поля, а само силовое поле при этом называется потенциальным, или консервативным; сила же потенциального силового поля называется потенциальной или консервативной силой.
Для того, чтобы стационарное силовое
поле было потенциальным необходимо и
достаточно, чтобы оно было безвихревым,
то есть сила
удовлетворяла следующим условиям:
;
;
()
Если использовать вектор вихря rot от вектора силы , то условие () можно переписать более кратко:
rot
5. Что называется потенциальной энергией и как определяется ее значение?
Потенциальной энергией в данной точке потенциального силового поля называется величина той работы, которую совершила бы сила поля при перемещении материальной точки из данной точки поля в ту, в которой потенциальная энергия условно принимается равной нулю.
- потенциальная энергия. Потенциальная
энергия П характеризует запас энергии
в данной точке поля.
Потенциальная энергия в какой-либо
точке поля с точностью до постоянной
равна силовой функции в той же точке,
взятой со знаком минус.
6. Как вычисляется работа потенциальных сил на конечном перемещении точки?
()
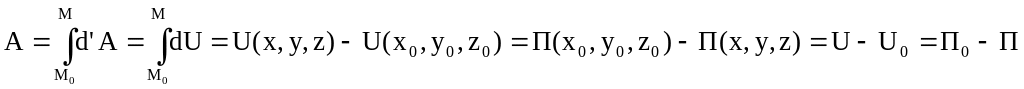- постоянные интегрирования, равные
значениям силовой функции и потенциальной
энергии в начальном положении точки.
Полная работа силы стационарного потенциального поля не зависит от формы траектории, по которой перемещается точка, и определяется лишь начальным и конечным положениями точки.
Из равенства () следует, что работа силы стационарного потенциального поля по любому замкнутому перемещению равна нулю.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Элементарная работа силы стационарного потенциального поля равная полному дифференциалу силовой функции.
10. Сформулируйте и запишите закон сохранения полной механической энергии точки.
Все силы, действующие на точку (внешние)
потенциальны, то есть существует такая
функция
,
что
;
;
.
Теорема о кинетической энергии для этой
точки:
Если точка движется в потенциальном
поле, то:
П - потенциальная энергия всех внешних сил, действующих на точку.
Следовательно:
Сумма кинетической и потенциальной энергии точки называется полной механической энергией E:
При движении материальной точки в потенциальном силовом поле ее полная механическая энергия постоянна.