2.3. Преломление и отражение радиоволны в ионосфере.

Электронная плотность ионосферы меняется с высотой, следовательно, и электрические свойства неоднородны по высоте.

Влияние неоднородности ионосферы проявляется в том, что радиоволны распространяются не по прямолинейным траекториям, а по криволинейным.

Рис. 2.4

Разобьем ионосферу на тонкие слои, в пределах каждого из которых диэлектрическую проницаемость будем считать постоянной.

Обозначим N₁ – электронная плотность 1-го слоя, N₂ –электронная плотность 2-го слоя и т.д.

Будем считать, что выполнится условие , а следовательно . Пусть на первый слой падает волна из неионизированного воздуха частоты f под углом .

На основании общего выражения диэлектрического для коэффициента преломления:

.

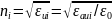
Применим к каждой границе закон синусов, получим:

После определенного числа преломлений угол у n–го слоя может сколь угодно близко подойти к

Полагая в (2.25) 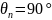и сохраняя крайние члены, получим:

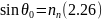
Данная формула выражает условие параллельности луча n–му слою.

В практике луч отражается от ионосферы (явление полного внутреннего отражения). Волна падает из более плотной среды в менее плотную и угол падения превышает критический угол:

Критический угол , но всегда , То есть полное внутреннее отражение наступает раньше, чем условие параллельности луча n–му слою (2.26).

Условие (2.26) можно записать, подставив в него выражение для , тогда:

(так как ).

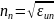Следовательно, при определенной электронной плотности слоя волна данной частоты отразится от более высоких слоев с более высокой только в том случае, если угол равен или превышает величину, определяемую формулой (2.28).

Из (2.28) найдем:

- максимальная рабочая частота, при заданной и произойдет отражение от данного слоя.

Если , то волна при заданной и не отразится.

Если волна нормально падает на ионосферу, то есть , то

, то есть отражение будет происходить на плазменной частоте .

Из (2.29) следует, что (закон Секанса):

- соотношение между наклонного луча и вертикального луча, которые отражаются от одной и той же области ионосферы.

Соотношение (2.30) часто называют законом секанса.

Чем больше электронная плотность, тем больше частота, для которой выполняется условие отражения.

Максимальная частота, при которой волна отражается в случае вертикального падения на ионосферный слой, называется критической частотой :

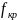1

- критическая частота.

Если рабочая частота > критической, то при нормальном падении волны на ионизированный слой отражений от него не происходит.

Критические частоты слоев D, E, F равны:

,

.

Если бы Земля и ионосфера были плоскими, то условие (2.30) всегда бы выполнялось. Сферичность же Земли и ионосферы ограничивают максимальный угол падения волны на ионосферу.

Рис. 2.5

Из рисунка видно, что луч, направленный по касательной к Земле, падает на ионосферу под наибольшим возможным углом при данной высоте слоя Н, то есть:

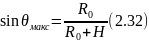
где – радиус Земли;

Н – высота нижней границы отражающего слоя ионосферы.

То обстоятельство, что волна не может быть послана под углом большим , приводит к ограничению рабочего диапазона частот.

При заданной максимальной электронной плотности , максимальная частота отраженной волны определяется формулой:

так, если отражение происходит на высоте Н=200 км, то .

Практически от ионосферы могут отражаться волны длиной 10 м.