2.4. Действующая длина симметричного вибратора.

Определим действующую длину симметричного вибратора для лю­бых направлений в экваториальной плоскости, то есть в плоскости, пер­пендикулярной оси вибратора и проходящей через его середину. В этой плоскости поля от любых отдельных элементов тока на больших рас­стояниях от вибратора не будут отличаться между собой по фазе.

Для определения действующей длины вибратора воспользуемся полученным выше выражением (1.23)

Подставив в это выражение формулы (2.2) для тока на вибраторе и произведя интегрирование, получим, что действующая длина, от­несенная к току в точках питания, равна

Учитывая, что при = 0

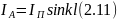
получаем

Если относить действующую длину к току в пучности, получаем из (1.23)

Зная действующую длину h_д симметричного вибратора и ток в точках питания, можно определить напряженность электрического поля в экваториальной плоскости вибратора (в свободном пространстве) с помощью выражения

В частном случае полуволнового вибратора ( )

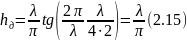
Для вибраторов малой длины ( ) получим, заменяя в (2.12) тан­генс аргументом,

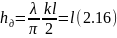
то есть действующая длина вибратора равна половине его геометрической длины.

2.5. Сопротивление излучения вибратора.

Сопротивление излучения является одним из основных параметров проволочной антенны. Как указывалось выше, сопротивлением излучения называется коэффициент, связывающий мощность излучения антенны с квадратом действующего значения тока.

Для расчета сопротивления излучения в теории антенн применяют­ся два метода: метод интегрирования вектора Пойнтинга и метод наводимых электродвижущих сил. В обоих случаях сопротивление излучения определяется по формуле

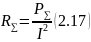
где I - действующее значение тока, к которому относится сопротив­ление . Однако способ определения мощности излучения антенны несколько отличается в каждом из упомянутых методов.

В этом параграфе излагается сущность метода интегрирования век­тора Пойнтинга и его применение для расчета симметричного вибра­тора. Идея метода заключается в следующем. Предполагается, что рассматриваемая антенна расположена в свободном неограниченном пространстве. Антенна мысленно окружается замкнутой поверхностью S (обычно сферой большого радиуса), и определяется поток мощности электромагнитных волн, проходящих через указанную сферу во внешнее пространство. Так как предполагается, что потери в про­странстве, окружающем антенну, отсутствуют, поток мощности яв­ляется мощностью излучения антенны:

Здесь П - численное значение вектора Пойнтинга, определяющее собой мощность, проходящую через единичную площадку, касатель­ную к поверхности сферы; для свободного пространства

где Е - действующее значение напряженности электрического поля на площадке.

Таким образом, произведение 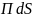определяет поток мощности через элементарную площадку dS, а интеграл (2.18) определяет всю мощность излучения антенны.

Подставляя (2.19) в (2.18), получаем

Рассчитаем рассмотренным методом сопротивление излучения тонкого симметричного вибратора с синусоидальным распределением тока. Действующее значение напряженности поля, создаваемого та­ким вибратором, можно определить с помощью выражения (2.7)

Учитывая, что в сферических координатах

получаем

Для симметричного вибратора 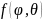не зависит от . Поэтому сопро­тивление излучения, отнесенное к току в пучности,

Интеграл в правой части равенства не выражается через элементар­ные функции. Произведя интегрирование, можно для 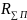получить следующее выражение:

где Six - интегральный синус от аргумента х; Cix - интегральный косинус; С = 0,577... - постоянная Эйлера.

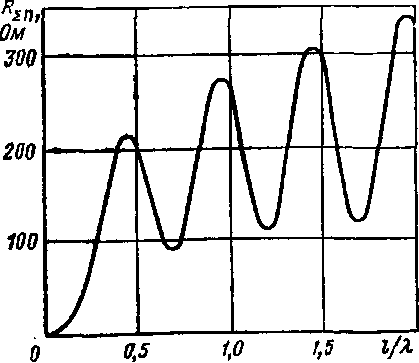
Рис. 2.7. Сопротивление излучения тонкого симметричного вибратора,

от­несенное к току в пучности, в зави­симости от .

Результаты вычислений по формуле (2.24) для в зависимости от приведены на рис. 2.7. Как видно из рисунка, при увеличении отношения вначале сопротив­ление излучения вибратора возра­стает. Это объясняется тем, что пока приблизительно меньше , ток по всей длине вибратора остается синфазным (то есть имеет одно направление вдоль провода) и с увеличением длины провода так же, как и в случае элементарного электрического диполя, мощность излучения и соответственно сопро­тивление излучения увеличивается. Когда длина вибратора стано­вится больше, чем , на вибраторе появляются участки с током про­тивоположной фазы, что при том же токе в пучности приводит к уменьшению мощности и сопротив­ления излучения. Так можно объяснить ход кривой в пределах 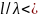0,75. При дальнейшем увеличении отношения кривая имеет колебательный характер с максимальными значениями при чет­ном числе и минимальными при нечетном числе полуволн, уклады­вающихся по длине вибратора.

Необходимо особо отметить два значения сопротивления излуче­ния: = 73,1 Ом для тонкого полуволнового вибратора и = 200 Ом для волнового (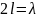 ). Эти цифры при­дется вспомнить при расчете некоторых параметров проволочных антенн.

Для короткого симметричного вибратора (практически при ) из (2.23) или (2.24) можно получить

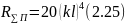
Зная сопротивление излучения вибратора, отнесенное к току в пуч­ности, легко найти приближенное значение активной составляющей входного сопротивления вибратора в средних точках питания. Если пренебречь потерями в антенне, активная составляющая входного сопротивления вибратора будет равна сопротивлению излучения , отнесенному к току I_А в точках питания. Для определения ука­занного сопротивления можно воспользоваться выражением для мощ­ности излучения через ток I_П в пучности и через ток I_А в точках питания

(2.26)

отсюда

Принимая, что ток на вибраторе распределен приблизительно по си­нусоидальному закону (2.11), получаем

Для полуволнового вибратора ( /4)

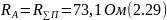
Для волнового вибратора ( ) по формуле (2.28) получается 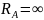. В действительности имеет конечное значение. Бесконечно большое значение получилось из-за предположения, что ток в точ­ках питания волнового вибратора равен нулю, а, как указывалось выше, ток в этом случае имеет хотя и малое, но конечное значение. Таким образом, формулой (2.28) можно пользоваться для приближен­ных вычислений лишь тогда, когда .

В заключение этого параграфа приведем простое выражение для расчета сопротивления излучения короткого (по сравнению с длиной волны) симметричного вибратора, отнесенного к току в точках пита­ния. Для этого подставим (2.25) в (2.28):

Последнее выражение совпадает с известным выражением для сопро­тивления излучения элементарного электрического диполя, находя­щегося в свободном пространстве, если под l понимать действующую Длину диполя, равную его геометрической длине. Напомним, что для короткого симметричного вибратора l обозначаем половину его длины.

Как показывает выражение (2.30), сопротивление излучения прямо пропорционально квадрату длины короткого вибратора и обратно пропорционально квадрату длины волны. Следовательно, проводник с током может эффективно излучать электромагнитные волны лишь тогда, когда его линейные размеры не слишком малы по сравнению с длиной волны.