Глава 2. Теория симметричного вибратора

2.1. Введение.

Симметричный вибратор представляет собой прямолинейный про­водник, у которого в симметричных (относительно середины) точках токи равны по величине и имеют одинаковое направление в пространст­ве. На рис. 2.1 показан пример распределения тока, характерного для симметричного вибратора. Здесь в симметричных точках и выполняется условие

Стрелки на рисунке показывают, что токи в указанных симметричных точках имеют одинаковое направление. Естественно, что это направле­ние показано для некоторого момента времени.

Для получения симметричного распределения тока в вибраторе можно, например, источник э.д.с. высокой частоты включить в его середину, как показано на рисунке. Однако в некоторых случаях сим­метричное распределение тока можно полу­чить и при других способах питания вибра­тора.

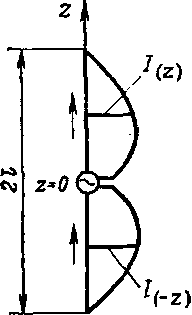
Рис. 2.1. Симметричный вибратор.

При исследовании симметричного вибра­тора, как и всякой другой антенны, нас в первую очередь будет интересовать вопрос о таких параметрах, как диаграмма направ­ленности, поляризация поля, действующая длина и входное сопротивление антенны. Ответ на вопрос об этих параметрах может быть сравнительно легко получен, если из­вестно распределение тока по длине вибра­тора. В самом деле, по известному току в проводе можно определить напряженность поля в дальней зоне и соответственно диа­грамму направленности (а также поляриза­цию поля). Отношение напряжения в точках питания к току в этих же точках определяет собой входное сопротивление антенны. Таким образом, прежде всего необходимо рассмотреть задачу о распреде­лении тока на симметричном вибраторе, возбуждаемом заданным источником э.д.с. Эта задача для цилиндрического вибратора про­извольной толщины является весьма сложной. Для тонких вибраторов конечной толщины распределение тока при вынужденных колебаниях может быть найдено в результате приближенного решения некоторого интегрального уравнения. Этот метод был развит в работах Галлена, Кинга и Гаррисона, а также Леонтовича и Левина и др.

2.2. Распределение тока и заряда на тонком вибраторе.

Строгая теория и опыт показывают, что на тонком симметричном вибраторе распределение тока имеет в первом приближении сину­соидальный характер и определяется выражением:

Здесь z - координата вдоль вибратора, отсчитываемая от его сере­дины (смотри рис. 2.1); - ток в пучности, находящейся на расстоянии четверти длины волны (λ) от изолированного конца вибратора.

На рис. 2.2 показано несколько примеров приближенного распре­деления тока на симметричном вибраторе, полученных на основании (2.2). Выражения (2.2) совпадают с соответствующим выражением для распределения тока в двухпроводной линии без потерь длиной 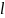, разомкнутой на конце. Симметричный вибратор можно получить, если провода отрезка линии раздвинуть, как показано на рис. 2.3.

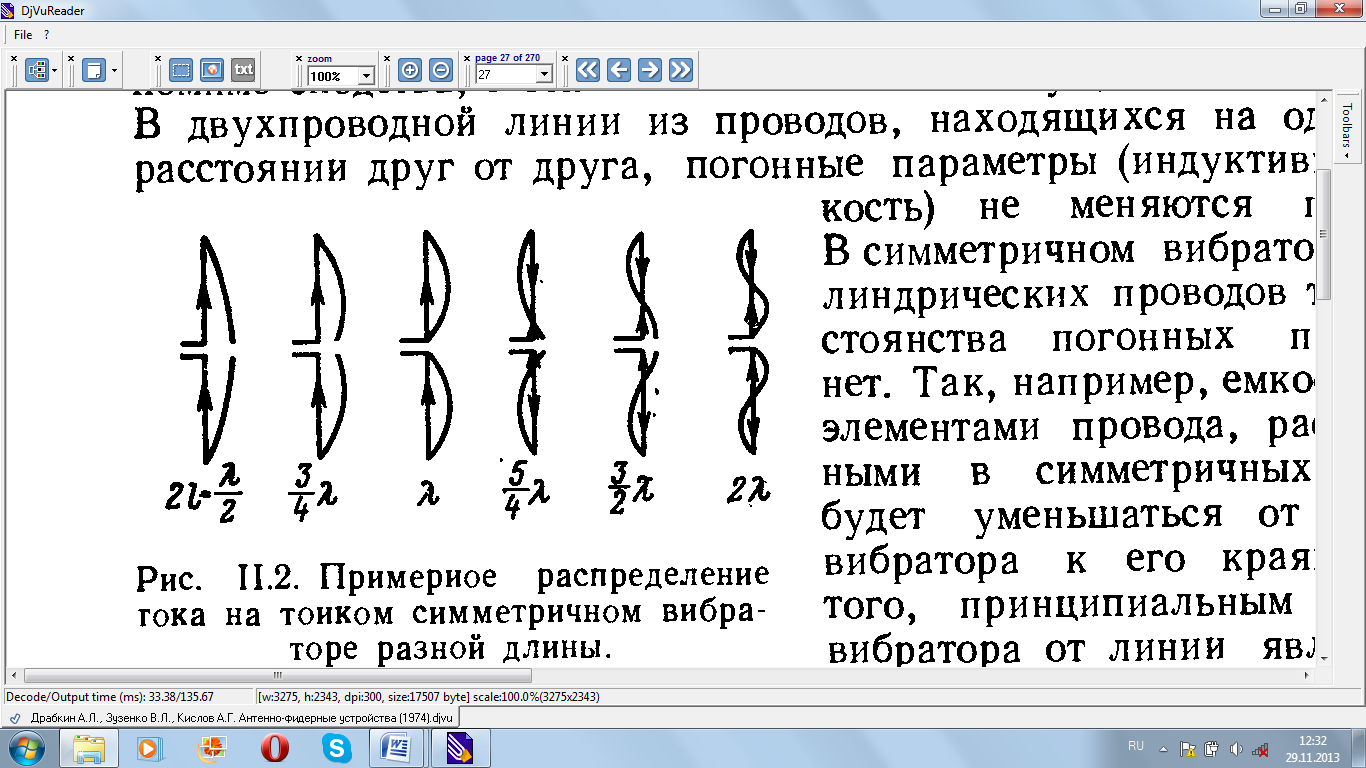
Рис. 2.2. Примерное распределение тока на тонком симметричном вибра­торе разной длины.

В отрезке линии и в вибраторе общим является то, что индуктивность и емкость распределены по их длине, это и обусловливает некоторое сходство в распределении тока по длине указанных систем. Однако, помимо сходства, в этих системах имеются и существенные различия. В двухпроводной линии из проводов, находящихся на одинаковом расстоянии друг от друга, погонные параметры (индуктивность, ем­кость) не меняются по длине. В симметричном вибраторе из ци­линдрических проводов такого по­стоянства погонных параметров нет. Так, например, емкость между элементами провода, расположен­ными в симметричных точках, будет уменьшаться от середины вибратора к его краям. Кроме того, принципиальным отличием вибратора от линии является то, что первый представляет собой излучающую систему, в то время как линия при достаточно малом расстоянии между проводами является системой неизлучающей.

В результате возникают некоторые различия в распределении тока по сравнению с синусоидальным. В узловых точках ток в нуль не обращается, а имеет конечное значение. Кроме того, минимум тока полу­чается на расстояниях от концов вибратора, несколько меньших чем 0,5 λ. Фаза тока не меняется скачком на 180°, а изменяется плавно. На рис. 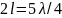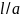2.4 для сравнения показаны кривые изменения амплитуды и фазы тока , на вибраторе длиной , построенные по (2.2) (сплошные) и рассчитанные строгим методом (пунктирные) при = 75, где а — радиус провода.

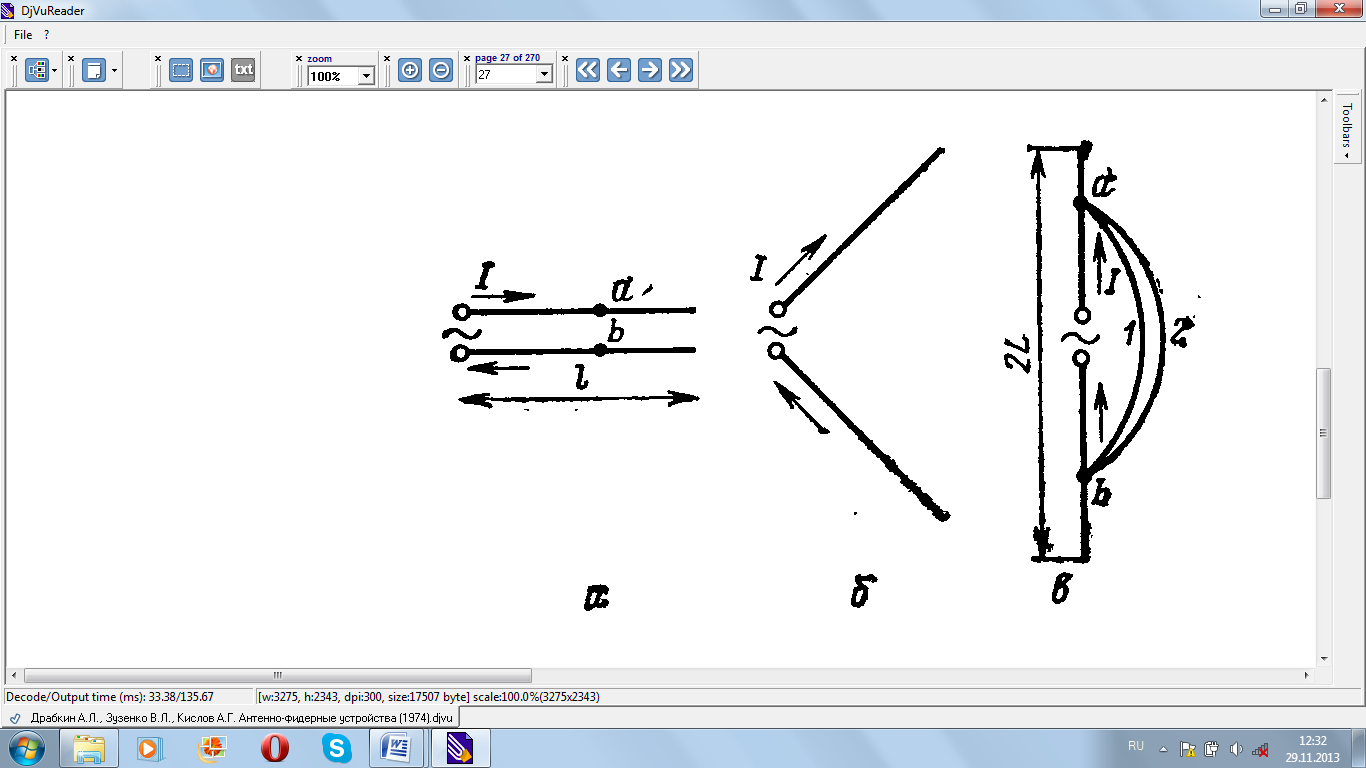
Рис. 2.3. Переход от разомкнутой двухпроводной линии (а) к симметричному вибратору (в).

В линии передачи наряду с распределением тока по длине рассмат­ривается также распределение напряжения. Напряжение в любом поперечном сечении линии ab (см. рис. 1.3, а) представляет собой раз­ность потенциалов, определяемую выражением:

где Е - напряженность электрического поля вдоль пути между точ­ками а и b; dl - элемент длины пути.

Поле между проводами линии в перпендикулярной к ним пло­скости носит электростатический характер, то есть является потенциаль­ным (обладает потенциалом). Поэтому разность потенциалов U_ab, определяемая интегралом (2.3), не зависит от пути интегрирования, если он лежит в одном и том же поперечном сечении и является вполне определенной величиной. Соответственно в замкнутом витке, помещен­ном в плоскости, перпендикулярной проводам линии передачи, э.д.с. наводиться не будет, так как виток не пронизывается магнитным пото­ком проводов линии.

Рис. 2.4. Кривые распределения амплитуд и фаз тока по длине симметричного вибратора длиной 5λ/4.

Симметричный вибратор (смотри рис. 2.3, в) создает электромагнитное поле излучения, которое не является потенциальным, и потому поня­тие напряжения и разности потенциалов здесь становится неопределен­ным. Действительно, значение интеграла (2.3), вычисленного между точками ab по пути 1 (смотри рис. 2.3), будет отличаться от значения интеграла, вычисленного по пути 2. Соответственно интеграл по замк­нутому контуру, образованному линиями 1,2, не будет равен нулю точно так же, как не будет равна нулю э.д.с. в приемном витке из провода, заменяющего контур 1,2, благодаря тому, что такой виток пронизывается переменным магнитным потоком вибратора.

Поэтому разность потенциалов между какими-либо двумя точками на вибраторе будет зависеть от выбранного пути и понятие напряже­ния между соответствующими точками вибратора получается неопре­деленным.

С некоторым допущением понятие напряжения можно применять для очень коротких вибраторов (по сравнению с длиной волны), так как поле вблизи такого вибратора будет в первом приближении по­тенциальным. Точно так же с достаточной определенностью можно го­ворить о напряжении между зажимами питания вибратора.

Для вибраторов, размеры которых соизмеримы с длиной волны, рассмотрение вопроса о распределении напряжения на вибраторе за­меняется исследованием распределения заряда. Отметим, что выводы теории однородных линий, сделанные для напряжения, остаются спра­ведливыми и для заряда, поскольку заряд на единицу длины линии равен напряжению между проводами, умноженному на погонную ем­кость линии.

Пример кривой распределе­ния заряда вдоль вибратора длиной показан на рис. 2.5. Как видно из рисунка, заряды в симметричных точках равны по вели­чине, но обратны по знаку.

Знание распределения заряда вдоль вибратора представляет инте­рес еще и потому, что величине поверхностной плотности заряда про­порциональна нормальная к проводу составляющая напряженности электрического поля. При больших значениях напряженности поля у поверхности провода вблизи него в воздухе наступает газовый разряд. Потери, возникающие при этом, а также перераспределение токов в антенне нарушают ее нормальную работу и являются недопустимыми. Заряд на проводе и соответственно напряженность поля у его поверх­ности пропорциональны току вибратора. С другой стороны, мощность излучения пропорциональна квадрату тока в антенне. По­этому предельно допустимые значения напряженности поля (при которых возникает газовый разряд) ограничивают величину мощности, которую можно подвести к антенне, без нарушения ее нормальной работы.

Рис. 2.5. Распределение заряда вдоль симметричного вибратора длиной .