1.3 Арифметические и логические основы эвм

1 Система счисления. Позиционные и непозиционные системы счисления

2 Перевод чисел из одной системы счисления в другую

3 Логические основы ЭВМ

Человеку издревле приходилось считать различные предметы, нужно было и записывать их количество. Самой первой, вероятно, возникла унарная(От лат. Unus -- один ) система записи, при которой числа обозначались соответствующим количеством черточек (или засечек на деревяшке).

Унарная запись получается очень громоздкой и неудобной, поэтому люди стали искать более компактные способы обозначать большие числа. Появились разные условные обозначения для различных чисел. Например, многие народы использовали в качестве цифр буквы, к которым добавляли специальные значки.

Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются.

Существуют позиционные и непозиционные системы счисления.

В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти. В римской системе счисления в качестве цифр используются латинские буквы I, V, X, L, С, D, М, в любой позиции означающие соответственно 1,5,10, 50, 100,500,1000.

Например, число 7 получается сложением пятерки и двух единиц, и отображается при записи в виде VII, а число 527 имеет вид DXXVII, где D - 500, XX - 20, V- 5, II - 2, то есть 527 -500 + 2-10 + 5 + 2-1. Таким образом, с увеличением изображаемых чисел быстро увеличивается количество необходимых для их записи символов. Однако главный недо­статок непозиционных систем - сложность проведения арифметических расчетов. Даже сложение и вычитание римских чисел (не говоря уже об умножении и делении) — это настоящее искусство, требующее спе­циальной профессиональной подготовки, которым в древности владели лишь немногие.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.

Одной из первых позиционных систем счисления была вавилонская шестидесятеричная. В ней использовались цифры двух видов, для изображения единиц и десятков. Следы вавилонской системы сохранились до наших дней в записи величины углов и промежутков времени. К древнему Вавилону восходит деление часа на 60 минут и угла на 360 градусов.

Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе.

За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д.

Основные позиционные системы счисления

Двоичная система.

Троичная система счисления. Использует три цифры – 0, 1 и 2, а также символы «+» и «–» для обозначения знака числа и запятую (точку) для разделения целой и дробной частей.

Система счисления с основанием 4.

Система счисления с основанием 7. Семь дней недели, семь нот, семь чудес Света, семь цветов радуги (хотя нормальный глаз видит их там только шесть, не разделяя оттенков синего и голубого) и многочисленные другие примеры указывают на то, что и это число служило разрядной единицей.

Восьмеричная система счисления.

Одиннадцатеричная система счисления употребляется в языке для устного счета народом маори – коренным населением Новой Зеландии.

Двенадцатеричная система счисления. На ее широкое использование в прошлом явно указывают названия числительных во многих языках, а также сохранившиеся в ряде стран способы отсчета времени, денег и соотношения между некоторыми единицами измерения. Год состоит из 12 месяцев, а половина суток состоит из 12 часов. В русском языке счет часто идет дюжинами, чуть реже гроссами (по 144=122), но в старину использовалось и слово для 1728=123. В английском языке есть особые (а не образованные по общему правилу) слова eleven (11) и twelve (12). Английский фунт состоит из 12 шиллингов.

Шестнадцатеричная система счисления.

Шестидесятеричная система счисления.

Почему люди пользуются десятичной системой счисления?

Выбор в качестве основания позиционной системы именно числа 10 объясняется традицией, а не какими-то особыми свойствами этого числа. Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления. Десятичная система счисления пришла из Индии, где она появилась не позднее VI в. н. э.

Более внимательный анализ правил чтения и записи чисел приводит к выводу: система счисления, которой мы обычно пользуемся, фактически является двойной, так как имеет основания – 10 и 1000. В частности, в русском языке известны названия только для первых семи разрядов десятичной системы счисления ( 1 – единица, 10 – десяток, 100 – сотня, 1000 – тысяча, 10000 – тьма, 100000 – легион, 1000000 – миллион ), но предпоследние два из них (легион и тьма) давно вышли из употребления, а соседние с ними (миллион и тысяча) – названия классов, а не только разрядов. Итак, фактически в русском языке остались лишь два самостоятельных названия для десятичных разрядов: десяток и сотня. В других языках – аналогичная ситуация.

Какие системы счисления используют специалисты для общения с компьютером?

Двоичная (используются цифры 0, 1 , а также символы «+» и «–» для обозначения знака числа и запятую (точку) для разделения целой и дробной части); Еще в 1673 г. немецкий философ и математик Лейбниц предложил использовать двоичную систему в качестве универсального логического языка.

Восьмеричная (используются цифры 0, 1, ..., 7) Широко использовалась в программировании в 1950-70-ые гг. К настоящему времени практически полностью вытеснена шестнадцатеричной системой счисления;

Шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, ..., 9, а для следующих чисел — от десяти до пятнадцати — в качестве цифр используются символы A, B, C, D, E, F). Внедрена американской корпорацией IBM. Широко используется в программировании для IBM-совместимых компьютеров.

Почему компьютеры пользуются не десятичной системой, а двоичной?

А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:

Для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;

Представление информации посредством только двух состояний надежно и помехоустойчиво;

Возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

Двоичная арифметика намного проще десятичной.

Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?

Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи. При записи чисел на бумаге использовать двоичную систему неудобно, так они получаются слишком длинными (сравните, например, числа 513 и 1000000001).

Вместе с тем, при тестировании аппаратных средств или отладке программ иногда возникает необходимость «заглянуть внутрь» электронной памяти, где вся информация представлена в виде длинных последовательностей нулей и единиц. Поэтому для удобства записи двоичных чисел используют системы счисления с основанием, представляющим собой степень двойки, прежде всего восьмеричную и шестнадцатеричную.

Cоответствие чисел, записанных в различных системах счисления

Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
1	001	1	1
2	010	2	2
3	011	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10

Перевод чисел из одной системы счисления в другую

Рассмотрим основные правила перевода:

• Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.

Пример. Число 22 перевести из десятичной в двоичную систему счисления

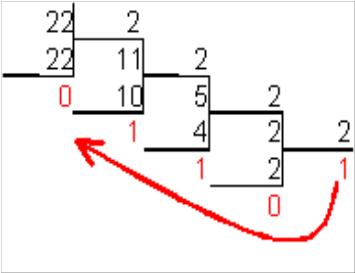
• Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8.

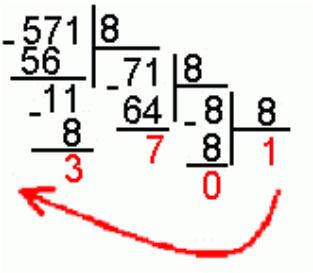
• Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16.

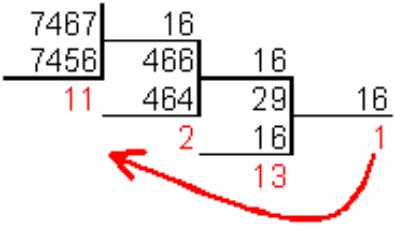
Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:

Пример . Число 11101000 из двоичной перевести в десятичную систему счисления.

• Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на  триады  (для восьмеричной) или  тетрады  (для шестнадцатеричной)  и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

• Например,

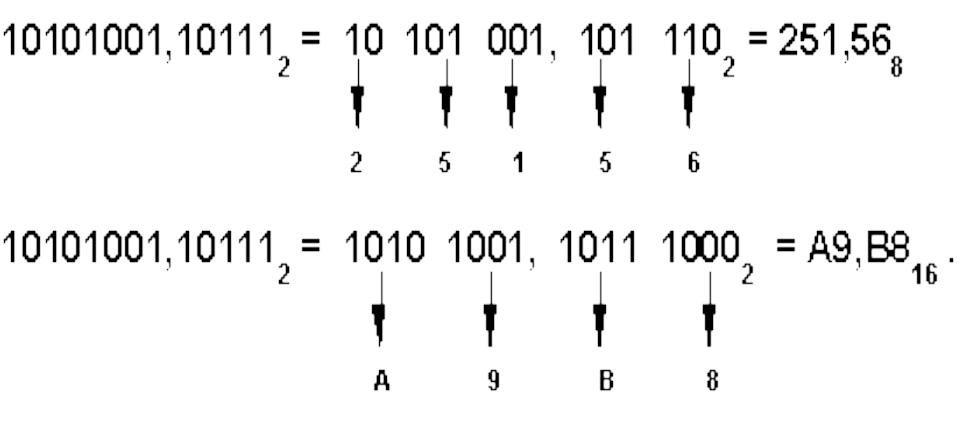
• Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр). Например:

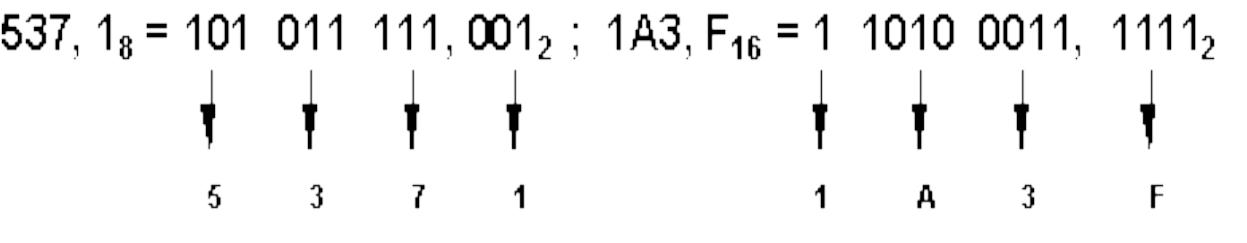
Арифметические операции в двоичной системе счисления:

Сложение			Умножение
+	0	1	*	0	1
0	0	1	0	0	0
1	1	10	1	0	1

Логические основы компьютеров. 

От логики - к алгебре логики.

• Основоположник логики – Аристотель.

• Рене Декарт - философ,математик,– рекомендовал в логике использовать математические методы.

• Лейбниц – математик,предложил использовать в логике математическую символику.Впервые высказал мысль о возможности применения в ней двоичной системы счисления.

• Джордж Буль - основоположник математической логики,создал Булеву алгебру – один из ее разделов.

Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.

Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo.

Так, например, предложение "6 — четное число" следует считать высказыванием, так как оно истинное. Предложение "Рим — столица Франции" тоже высказывание, так как оно ложное.

Алгебра логики рассматривает любое высказывание только с одной точки зрения — является ли оно истинным или ложным.

Логические связки.

Слова и словосочетания "не",   "и",   "или",  "если... , то",   "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются   логическими связками.

Bысказывания, образованные из других высказываний с помощью логических связок, называются   составными. Высказывания, не являющиеся составными, называются   элементарными.

Так, например, из элементарных высказываний "Петров — врач", "Петров — шахматист" при помощи связки "и" можно получить составное высказывание "Петров — врач и шахматист", понимаемое как "Петров — врач, хорошо играющий в шахматы".

При помощи связки "или" из этих же высказываний можно получить составное высказывание "Петров — врач или шахматист", понимаемое в алгебре логики как "Петров или врач, или шахматист, или и врач и шахматист одновременно".

Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.

Чтобы обращаться к логическим высказываниям, им назначают имена. Пусть через А обозначено высказывание "Тимур поедет летом на море", а через В — высказывание "Тимур летом отправится в горы". Тогда составное высказывание   "Тимур летом побывает и на море,  и в горах"   можно кратко записать как     А и В.  Здесь   "и"  — логическая связка,   А,   В   — логические переменные, которые мoгут принимать только два значения —   "истина"   или   "ложь",  обозначаемые, соответственно,   "1"  и   "0".

Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение:

• НЕ    Операция, выражаемая словом "не", называется отрицанием и обозначается чертой над высказыванием.   Высказывание истинно, когда A ложно, и ложно, когда A истинно.   Пример. "Луна — спутник Земли" (А); "Луна — не спутник Земли" ( ) .

• И    Операция, выражаемая связкой "и", называется конъюнкцией (лат. conjunctio — соединение) или логическим умножением и обозначается точкой " . " (может также обозначаться знаками ^ или &). Высказывание истинно тогда и только тогда, когда оба высказывания А и В истинны.

• ИЛИ    Операция, выражаемая связкой "или" (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение) или логическим сложением и обозначается знаком v (или плюсом). Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны.  

• ЕСЛИ-ТО   Операция, выражаемая связками   "если ..., то",  "из ... следует",  "... влечет ...",  называется импликацией (лат. implico — тесно связаны) и обозначается знаком . Высказывание   ложно тогда и только тогда, когда  А  истинно,  а  В  ложно.

Каким же образом импликация связывает два элементарных высказывания? Покажем это на примере высказываний: "данный четырёхугольник — квадрат" (А) и "около данного четырёхугольника можно описать окружность" (В). Рассмотрим составное высказывание  , понимаемое как "если данный четырёхугольник квадрат, то около него можно описать окружность". Есть три варианта, когда высказывание   истинно:

1. А истинно и В истинно, то есть данный четырёхугольник квадрат, и около него можно описать окружность;

2. А ложно и В истинно, то есть данный четырёхугольник не является квадратом, но около него можно описать окружность (разумеется, это справедливо не для всякого четырёхугольника);

3. A ложно и B ложно, то есть данный четырёхугольник не является квадратом, и около него нельзя описать окружность.

Ложен только один вариант, когда А истинно, а В ложно, то есть данный четырёхугольник является квадратом, но около него нельзя описать окружность.

РАВНОСИЛЬНО   Операция, выражаемая связками "тогда и только тогда", "необходимо и достаточно", "... равносильно ...", называется эквиваленцией или двойной импликацией и обозначается знаком    или  ~.  

Высказывание истинно тогда и только тогда, когда значения А и В совпадают.       Например, высказывания     "24 делится на 6 тогда и только тогда, когда 24 делится на 3",    "23 делится на 6 тогда и только тогда, когда 23 делится на 3"   истинны,   а высказывания   "24 делится на 6 тогда и только тогда, когда 24 делится на 5",   "21 делится на 6 тогда и только тогда, когда 21 делится на 3"   ложны.

Итак, нами рассмотрены пять логических операций: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция.

Операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.

Какая связь между алгеброй логики и двоичным кодированием?

Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.

Из этого следует, что одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных.

Данные и команды представляются в виде двоичных последовательностей различной структуры и длины.

В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули (или наоборот), например:

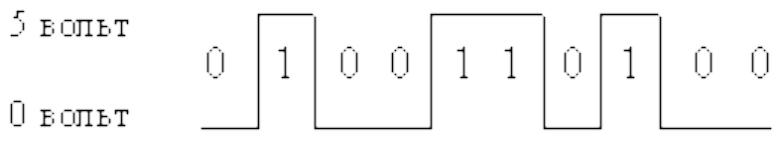
Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию.

Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также триггер.

С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.

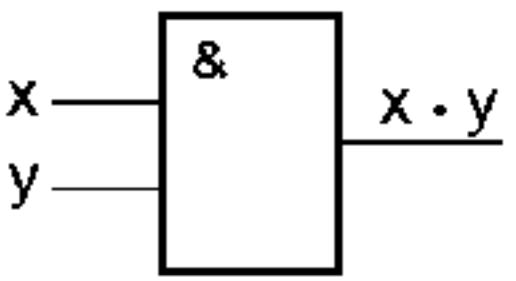
• Схема И реализует конъюнкцию двух или более логических значений:

  Схема И	Таблица истинности схемы И
  	x y 0 0 0 0 1 0 1 0 0 1 1 1

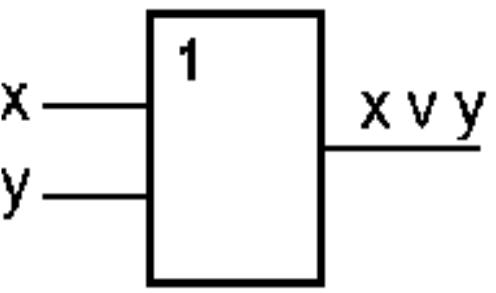
• Схема  ИЛИ  реализует дизъюнкцию двух или более логических значений:

Схема ИЛИ	Таблица истинности схемы ИЛИ
	x y x v y 0 0 0 0 1 1 1 0 1 1 1 1

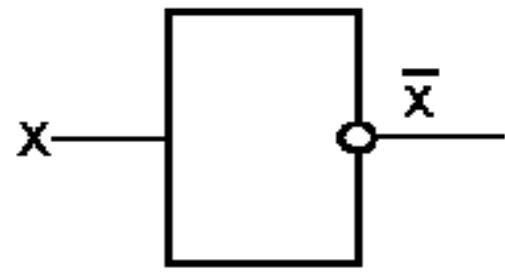
• Схема   НЕ  (инвертор) реализует операцию отрицания.   читается как "не х"  или  "инверсия х". 

Схема НЕ	Таблица истинности схемы НЕ
	0 1 1 0
Если на входе схемы  0,  то на выходе  1  Когда на входе  1,  на выходе  0

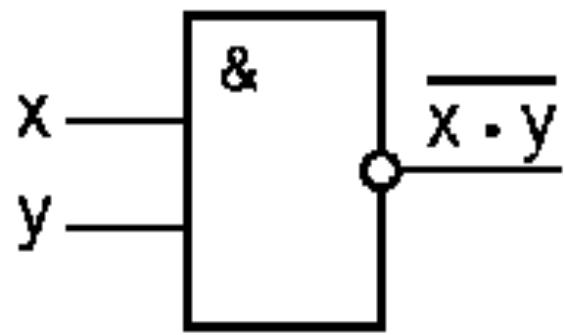
• Схема И—НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И:

Схема И—НЕ	Таблица истинности схемы И—НЕ
	y 0 0 1 0 1 1 1 0 1 1 1 0

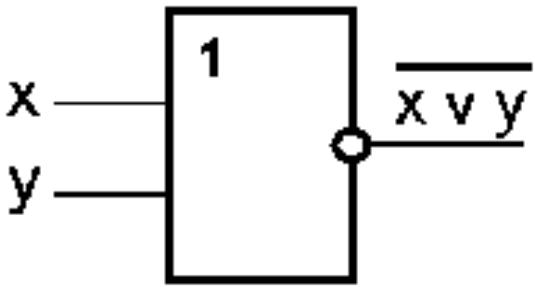
• Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора  и осуществляет отрицание результата схемы ИЛИ:

Схема ИЛИ—НЕ	Таблица истинности схемы ИЛИ—НЕ
	y 0 0 1 0 1 0 1 0 0 1 1 0

Триггер — это электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю.

Самый распространённый тип триггера — так называемый RS-триггер. Он имеет два симметричных входа S и R и два симметричных выхода Q и , причем выходной сигнал Q является логическим отрицанием сигнала .

На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов.

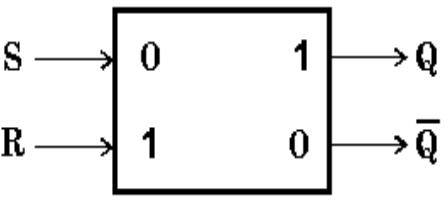
Регистр – узел ЭВМ,состоящий из триггеров,предназначенный для запоминания многоразрядных кодов и выполнения над ними некоторых логических преобразований.

Сумматор — это электронная логическая схема, выполняющая суммирование двоичных чисел.

Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах машины.

Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров.