Интервальное статическое распределение выборки

При большом числе наблюдений и большом числе вариант удобно варианты группировать по отдельным интервалам их значений. Для этого шкала интересующего нас признака разделяется на некоторое число интервалов, и вместо отдельных вариант рассматриваются группы значений вариант, попавших в последовательно расположенные интервалы.

Число m таких интервалов, как правило, берётся в пределах от 10 до 20. Ширина интервалов hx определяется по формуле

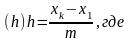хк-х1 – размах выборки; m – число интервалов.

В таких случаях составляется статическое распределение выборки по частотам интервалов (интервальное статическое распределение выборки). При этом частота интервала равна сумме частот вариант, попавших в данный интервал.

Exp: Для выборки примера 2 составить таблицу статического распределения по интервалам, беря число интервалов m=10.

Вычислим ширину интервалов:

(h)=

[7,4;7,5]	1	(9,5;10,0]	3
(7,5;8,0]	1	(10,0;10,5]	2 (**)
(8,0;8,5]	1	(10,5;11,0]	1
(8,5;9,0]	2	(11,0;11,5]	3
(9,0;9,5]	2	(11,5;12,0]	4

Графики вариационных рядов

Если на оси абсцисс прямоугольной системы координат расположить варианты х_i, а на оси ординат – соответствующие им частотs n_i, то в плоскости получим точки (х_i,n_i) . Соединяем точки (х_i,n_i) отрезками.

Df: Ломаная линия, отрезки которой соединяют точки (х_i,n_i), называется полигоном частот.

Если на оси ординат отложить относительные частоты _i, то получим полигон относительных частот.

Exp: Построить полигон частот и полигон относительных частот для статического распределения выборки, заданной таблицей (*)

Т.к. , то ординаты точек (хi, i) получаются из ординат точек (хi,ni) уменьшением их в n раз. Следовательно, полигон частот (в системе координат) будет представлять полигон относительных частот в системе координат, y которой масштаб на оси ординат увеличен в n раз.

Если статическое распределение выборки задаётся в виде последовательности интервалов значений вариант и их частот, то геометрическое изображение даётся при помощи гистограммы частот.

Df: Гистограммой частот называют ступенчатую фигуру, состоящую их прямоугольников, построенных на частичных интервалах с длиной h и высотой, равной отношению (плотность частоты на данном интервале).

Площадь i-го частичного прямоугольника равна . Значит, площадь гистограммы частот равна сумме всех частот, т.е. объёму выборки.

Exp: Построить гистограмму частот статического распределения, заданного таблицей (*,*)

4. Числовые характеристики выборки.

1. Выборочным средним выборки объема n со статическим распределением (***)

(***)

Хi	x1	x2	…	xn
ni	n1	n2	…	nk

xi	x1	x2	…	x (****) k
Ni	N1	N2	…	Nk

называется среднее арифметическое значений признака выборки, т.е.

…(1)

Аналогично, для генеральной совокупности объема N со статическим распределением (****) определяется генеральное среднее:

…(2)

Exp: Вычислить выборочное среднее для выборки и генеральное среднее для генеральной совокупности из exp3.

2. Выборочная и генеральная дисперсия.

Df: Выборочной дисперсией Dв некоторой выборки называют среднее арифметическое квадратов отклонений значений признака от выборочной средней , т.е.

…(3)

Аналогично, для генеральной совокупности определяют генеральную дисперсию Dг

…(4)

Дисперсия является характеристикой рассеяния значений признака вокруг своего среднего значения.

Exp: Вычислить выборочную и генеральную дисперсии для выборки и генеральной совокупности из exp3.

Из предыдущего примера имеем =4,52; =4,44

Для вычисления дисперсий (выборочной или генеральной) имеется удобная формула, которая даётся следующей теоремой:

Теорема. Дисперсия равна разности среднего арифметического значения квадратов признака и квадрата среднего значения признака:

…(5)

Exp: Вычислить дисперсии для выборки и генеральной совокупности из exp3