Теория графов – одна из редких математических дисциплин, для которых можно указать точную дату рождения. В 1736 г. в трудах Академии наук Санкт-Петербурга была опубликована статья Леонарда Эйлера, посвящённая задаче о Кенигсбергских мостах. В те времена Кенигсберг, нынешний Калининград, располагался в Восточной Пруссии. Семь мостов соединяли берега и два острова реки Преголи, на которых располагался Кенигсберг. Эйлер задался вопросом, можно ли, выйдя из дома, пройти по каждому мосту в точности по одному разу и вернуться домой. Ответ на этот вопрос оказался отрицательным, что будет понятно после ознакомления с задачей почтальона, изложенной в гл. 6. Решая эту задачу, Эйлер впервые применил модель графа. На рубеже XIX и XX вв. теория графа получила стремительное развитие в связи со становлением теории электрических цепей и распространением представлений о молекулярном строении вещества. К середине ХХ в. в теории графов сложились два существенно различных направления: алгебраическое и оптимизационное. В данном пособии будут рассматриваться только оптимизационные задачи теории графов.

Граф – это совокупность множества Х, элементы которого называются вершинами, и множества А упорядоченных пар вершин, элементы которого называются дугами. Граф обозначается как (Х,А).

Вершины, как правило, обозначаются строчными латинскими буквами, а дуги – строчными греческими буквами.

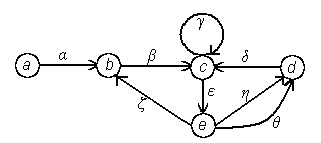
Рис. 1.1.

Дуга также может быть обозначена парой латинских букв, соответствующих обозначению начальной и конечной вершинам этой дуги. Например, на рис. 1.1 дуга  β может быть обозначена через (b, c). Если две вершины соединяются (в одном направлении) несколькими дугами, то последние могут быть представлены упорядоченной парой соответствующих вершин с различными индексами. Так, на рис. 1.1 дуга  η  может быть обозначена через  (e, d)₁, а дуга  θ  – через  (e, d)₂.

Некоторые задачи теории графов требуют наличия информации только о концевых точках дуг, т.е. нет необходимости различать начало и конец дуги и приписывать дугам определенные направления. Граф (Х,Е), в котором направления дуг не задаются, называется неориентированным. Неориентированные дуги называются ребрами. Е – множество ребер.

Дуга, начальная и конечная вершины которой совпадают,  называется  петлей.  На рис. 1.1 дуга  γ  является петлей.

Вершина и дуга инцидентны друг другу, если вершина является для этой дуги концевой или начальной. На рис. 1.1 вершина  b  и дуга  α  инцидентны друг другу.

Две дуги инцидентны друг другу, если обе они инцидентны одной и той же вершине. На рис. 1.1  дуги  ζ  и  ε  инцидентны друг другу.

Две вершины – соседние или смежные, если есть дуга, их соединяющая. На рис. 1.1 вершины  e  и  d  соседние, т.к. дуга  η  их соединяет.

Пусть х₁, x₂, …, x_n+1 - произвольная последовательность вершин; цепью называется любая последовательность дуг α₁, α₂, …, α_n, такая, что концевыми точками дуги α_i являются вершины x_i  и x_i+1, т.е. α_i=(x_i , x_i+1) или α_i=(x_i+1 , x_i) для i=1,n. Вершина х₁ называется начальной вершиной цепи, а вершина х_n+1 - конечной вершиной цепи. Длина цепи равна числу входящих в неё дуг. Так, на рис. 1.1 последовательность дуг  α, β, δ, η  образует цепь длины 4, которая соединяет вершину  a  с вершиной  e.

Цепь, для которой α_i=(x_i , x_i+1) при всех i=1,n, есть путь. Длина пути, его начальная и конечная вершины определяются так же, как и для цепи. На рис. 1.1 дуги  β, ε, η  образуют путь длины 3, соединяющий вершину  b  с вершиной  d.

Циклом называется цепь, у которой начальная и конечная вершины совпадают. Контуром называется путь, у которого начальная и конечная вершины совпадают. На рис. 1.1 дуги  β, δ, η, ζ  образуют цикл длины 4, а дуги  δ, ε, η – контур длины 3.

Цепь, цикл, путь или контур называются простыми, если ни одна вершина не инцидентна более чем двум входящим в нее дугам (т.е. если цепь, цикл, путь или контур не содержат внутри себя циклов). Например, на рис. 1.1 цепь  β, δ, θ   и контур  η, δ, ε,  – простые, а цикл  θ, ζ, β, ε, η  и путь  β, γ, ε  простыми не являются.

Граф называется связным, если в нем для каждой пары вершин найдется соединяющая их цепь. Граф на рис. 1.1 является связным, а граф на рис. 1.2 является несвязным, т.к. в нём отсутствует цепь, соединяющая вершины  с  и  е.

Рис. 1.2.

Любой граф можно рассматривать как некоторую совокупность связных графов. Каждый из этих графов называется компонентом исходного графа. Граф на рис. 1.2 имеет два компонента.

Пусть X^/  – подмножество множества X графа G=(X,A).  Граф, множество вершин которого совпадает с X^/, а множество дуг включает все дуги множества A, обе концевые вершины которых принадлежат X^/, называется подграфом графа G, порожденным X^/. Пусть A^/ – подмножество множества A графа G=(X,A). Граф, множество дуг которого совпадает A^/, а множество вершин состоит из вершин, инцидентных дугам из A^/, называется подграфом графа G, порожденным A^/. Например, для графа, изображённого на рис. 1.1, подграф, порождённый подмножеством вершин {b, c, d}, изображён на рис. 1.3, подграф, порождённый подмножеством дуг  {θ, ζ, β, ε, η}, – на рис. 1.4.

Рис. 1.3.

Рис. 1.4.

Совокупность дуг называется деревом, если она, во-первых, порождает связный граф, и, во-вторых, не содержит циклов.  Для графа  с рис. 1.1 деревьями, например, являются: {α, β, δ }, {α, β, ζ, η }, {δ, ζ, η}. Совокупность же дуг {β, δ, ε, η} деревом не является, т.к. содержит цикл {δ, ε, η}.

Лесом называется любая совокупность дуг, не содержащая циклов. Таким образом, лес состоит из одного или большего числа деревьев. Например, для графа, изображённого на рис. 1.2, совокупность дуг {β, γ, δ, ε, η} является лесом, состоящим из двух деревьев.

Покрывающим деревом графа G называется  любое дерево, порождающее подграф, множество вершин которого совпадает со множеством вершин графа G.  Так, для графа с рис. 1.1 покрывающим деревом является {α, ε, ζ, θ}.

Очевидно, что граф, состоящий более чем из одного компонента, не имеет покрывающего дерева. Любой же связный граф обязательно содержит некоторое покрывающее дерево.

Дерево, состоящее из одной дуги, включает две вершины.

Дерево, состоящее из двух дуг, включает три вершины.

Дерево, состоящее из (n-1) дуг, включает n вершин.

Следовательно, любое покрывающее дерево связного графа, имеющего n вершин, состоит из (n–1) дуги.

Множество дуг, исключение которых из графа увеличивает число его компонентов, называется разрезом. Разрез, который не содержит в качестве собственного подмножества никакого другого разреза, называется простым разрезом. Например, для графа на рис. 1.1 {β, δ, ε, ζ} – разрез, а {δ, ε, ζ} – простой разрез.

Удобным способом описания графа является его матричное представление. Пусть G – произвольный граф без петель, состоящий из  m  вершин и  n  дуг.

Назовём матрицей инциденций графа G матрицу, состоящую из m строк, каждая из которых соответствует определенной вершине, и n столбцов, каждый из которых соответствует определенной дуге. Элемент матрицы  (i,j) равен: +1, если i-я вершина является начальной для j-й дуги; -1, если i-я вершина является конечной для j-й дуги;  0, если i-я вершина и j-я дуга не инцидентны. Для графа с рис. 1.2 матрица инциденций имеет вид:

	β	β	γ	δ	ε	ζ	η
a	–1	0	0	+1	0	0	0
b	+1	–1	0	0	0	0	0
c	0	+1	+1	0	0	0	0
d	0	0	–1	–1	0	0	0
e	0	0	0	0	–1	–1	0
f	0	0	0	0	+1	0	+1
g	0	0	0	0	0	+1	–1

Матрицей смежности неориентированного графа G называется квадратная матрица порядка  m, элемент  (i,j)  которой равен единице, если i-я и j-я вершины – соседние, и нулю, в противном случае. В случае ориентированного графа G элемент  (i,j)  матрицы смежности равен единице при наличии дуги из вершины i в вершину j и равен нулю в противном случае.

Аналогично определяется и квадратная порядка n матрица инцидентности дуг или ребер графа.

2. Алгоритмы построения деревьев

2.1. Неориентированные покрывающие деревья

Пусть в неориентированном графе G=(X,E) каждому ребру (x,y) приписан вес a(x,y). Тогда  вес дерева  – это сумма весов ребер, его составляющих.

Совокупность дуг называется деревом, если она, во-первых, порождает связный граф, и, во-вторых, не содержит циклов.

Суть алгоритма построения покрывающего дерева состоит в просмотре ребер графа, в процессе которого относительно каждого ребра принимается решение о том, будет ли оно включено в дерево. Это можно представить как процесс окрашивания ребер в два цвета: голубой – для включаемых в дерево рёбер и оранжевый – для не включаемых. При просмотре ребра проверяется, не образует ли данное ребро в совокупности с уже включенными в дерево (голубыми) ребрами цикл. Если нет, окрашиваем в голубой цвет, да – в оранжевый. Голубые ребра составляют граф, имеющий один или несколько связных компонентов. Вершины отдельного компонента – “букет”. Алгоритм заканчивает работу, когда число голубых ребер на единицу меньше числа вершин графа или когда все вершины графа оказываются в одном букете. Эти условия эквивалентны и относятся к случаю, когда граф содержит покрывающее дерево. Если же граф такого дерева не содержит, т.е. является несвязным, работа алгоритма заканчивается после окраски всех ребер графа.

Процедура  алгоритма

Перед началом работы ребра не окрашены и букеты не сформированы.

Шаг 1. Выбрать любое ребро, не являющееся петлей, окрасить его в голубой цвет и сформировать букет из концевых вершин этого ребра.

Шаг 2. Выбрать любое неокрашенное ребро, не являющееся петлей. (Если в графе такого ребра не найдется, закончить процедуру: исходный граф не содержит покрывающего дерева.)  Возможны 4 случая:

а) обе концевые вершины выбранного ребра принадлежат одному и тому же букету - окрасить ребро в оранжевый цвет – и на шаг 2;

б) одна из концевых вершин ребра принадлежит некоторому букету, а другая не принадлежит ни одному из уже сформированных букетов - окрасить ребро в голубой цвет, вторую вершину включить в тот же букет – и на шаг 3;

в) ни одна из концевых вершин не принадлежит ни одному из сформированных букетов - окрасить ребро в голубой цвет, сформировать новый букет из этих вершин – и на шаг 3;

г) концевые вершины ребра принадлежат различным букетам - окрасить ребро в голубой цвет, оба букета соединить в один новый – и на шаг 3;

Шаг 3. Если все вершины графа вошли в один букет, закончить процедуру: голубые ребра образуют покрывающее дерево. В противном случае – на шаг 2.

Пример. Построить покрывающее дерево для графа, изображённого на рис. 2.1.

Рис. 2.1.

Будем рассматривать рёбра графа в произвольно выбранном порядке. Заметим, что (a,b)₁ – обозначение ребра с весом 1, соединяющего вершины a и b, а (a,b)₂ – ребра с весом 2, соединяющего те же вершины. То есть ребру большего веса соответствует больший индекс. Аналогично обозначены рёбра (c,d)₁, (c,d)₂ и (e,f)₁, (e,f)₂.

Ход выполнения алгоритма приводится в таблице:

Ребро	Цвет	Букет 1	Букет 2
		Сначала пуст	Сначала пуст
(a,b)1	Голубой	a, b	Пуст
(a,c)	Голубой	a, b, c	Пуст
(h,g)	Голубой	a, b, c	h, g
(g,f)	Голубой	a, b, c	h, g, f
(b,c)	Оранжевый	a, b, c	h, g, f
(c,d)2	Голубой	a, b, c, d	h, g, f
(c,h)	Голубой	a, b, c, d, h, g, f	Пуст
(d,e)	Голубой	a, b, c, d, h, g, f, e	Пуст

Поскольку после просмотра ребра (d,e) все вершины графа попали в один букет, алгоритм заканчивает работу. На рис. 2.2 приведено полученное покрывающее дерево для графа, изображённого на рис. 2.1, составленное из рёбер, окрашенных в голубой цвет.

Рис. 2.2.

В алгоритме построения произвольного покрывающего дерева ребра просматривались в произвольном порядке. Если в данном алгоритме просматривать ребра в порядке возрастания их весов: первое ребро – с минимальным весом, а последнее – с максимальным, при этом ребра с одинаковыми весами упорядочивать произвольно, то в результате будет получено минимальное покрывающее дерево. Если же ребра графа просматриваются в порядке убывания их весов, то в результате будет получено максимальное покрывающее дерево.

Ход выполнения алгоритма получения минимального покрывающего дерева для графа, изображённого на рис. 2.1, приводится в таблице:

Ребро	Цвет	Букет 1	Букет 2	Букет 3	Вес голубого ребра
		Сначала пуст	Сначала пуст	Сначала пуст
(a,b)1	Голубой	a, b	Пуст	Пуст	1
(c,d)1	Голубой	a, b	c, d	Пуст	1
(e,f)1	Голубой	a, b	c, d	e, f	1
(b,c)	Голубой	a, b, c, d	Пуст	e, f	2
(a,b)2	Оранжевый	a, b, c, d	Пуст	e, f
(c,d)2	Оранжевый	a, b, c, d	Пуст	e, f
(e,f)2	Оранжевый	a, b, c, d	Пуст	e, f
(h,c)	Голубой	a, b, c, d, h	Пуст	e, f	3
(g,f)	Голубой	a, b, c, d, h	Пуст	e, f, g	3
(d,e)	Голубой	a, b, c, d, h, e, f	Пуст	Пуст	3

Полученное для графа, изображённого на рис. 2.1, минимальное покрывающее дерево, вес которого равен 14, приведено на рис. 2.3.

Рис. 2.3.

Ход выполнения алгоритма получения максимального покрывающего дерева для графа, изображённого на рис. 2.1, приводится в таблице:

Ребро	Цвет	Букет 1	Букет 2	Вес голубого ребра
		Сначала пуст	Сначала пуст
(a,c)	Голубой	a, c	Пуст	5
(h,g)	Голубой	a, c	h, g	5
(h,c)	Голубой	a, c, h, g	Пуст	3
(g,f)	Голубой	a, c, h, g, f	Пуст	3
(d,e)	Голубой	a, c, h, g, f	d, e	3
(b,c)	Голубой	a, c, h, g, f, b	d, e	2
(a,b)2	Оранжевый	a, c, h, g, f, b	d, e
(c,d)2	Голубой	a, c, h, g, f, b, d, e	Пуст	2

Полученное для графа, изображённого на рис. 2.1, максимальное покрывающее дерево, вес которого равен 23,  приведено на рис.2.4.

Рис. 2.4.

Обоснование алгоритма построения минимального дерева

Пусть х₁, x₂, …, x_n+1 - произвольная последовательность вершин; цепью называется любая последовательность дуг α₁, α₂, …, α_n, такая, что концевыми точками дуги α_i являются вершины x_i  и x_i+1, т.е. α_i=(x_i , x_i+1) или α_i=(x_i+1 , x_i) для i=1,n. Вершина х₁ называется начальной вершиной цепи, а вершина х_n+1 - конечной вершиной цепи.

Циклом называется цепь, у которой начальная и конечная вершины совпадают.

Пусть алгоритм строит дерево Т, а минимальное на самом деле дерево S. Так как T и S различны, то они отличаются, по крайней мере, одним ребром. Пусть ребро  e₁=(x,y) – первое из просмотренных в алгоритме, которое содержится в T, но не содержится в S. S – покрывающее дерево, поэтому в нем содержится цепь (единственная), соединяющая вершины x и y: c(x,y), Прибавим e₁  к S, тогда е₁ вместе с с(х,у) образует цикл. Так как Т – дерево и не содержит циклов, то в цикле (е₁,с(х,у)) должно содержаться хотя бы одно ребро, не присутствующее в Т, пусть это будет ребро е₂. Исключим из S ребро е₂. Получилось дерево S^/. Так как по предположению дерево S минимально, то вес S^/  не меньше веса S,  т.е. а(е₁) ≥ а(е₂). В этом случае в алгоритме построения Т ребро е₂ было просмотрено раньше, чем е₁, но не было включено в Т, т.е. составляло цикл с уже просмотренными и включенными в Т ребрами. Это противоречие,  т.к. ребра, с которыми е₂  составляет цикл в Т, входят в S, ведь е₁ – первое из просмотренных ребер, содержащееся в Т, но не содержащееся в S. В S существование цикла невозможно. Отсюда следует, что  е₂  просматривалось позже, чем е₁, т.е. а(е₂) ≥ а(е₁).  Значит,  а(е₂) = а(е₁).  Вес S^/ равен весу S, при этом у S^/  общих ребер с Т на одно больше. Если все  эти рассуждения повторить для случая, когда S^/ – минимальное дерево, будет построено дерево S^// того же веса, в котором еще на одно общее с Т ребро больше. И т.д., пока мы не получим минимальное покрывающее дерево, полностью совпадающее с Т.

Что касается алгоритма построения максимального дерева, то его обоснование совпадает с приведенным, если заменить слово «минимальный» на «максимальный» и поменять знаки неравенств на противоположные.