Оглавление

Введение. 2

Краткие теоретические сведения. 3

Спецификация теста 11

Демонстрационный вариант контрольных измерительных материалов по дисциплине «Дискретная математика» 15

Система оценивания демонстрационного варианта контрольных измерительных материалов по дисциплине «Дискретная математика» 19

Заключение. 21

Список литературы………………………………………………………22

Введение.

Тема данной курсовой работы « Разработка теста итогового контроля по теме «Теория множеств»».

Актуальность данной курсовой работы определяется тем, что в настоящее время ведется серьезная исследовательская и практическая работа по разработке различных систем педагогического мониторинга, построенные преимущественно на нормативном тестовом контроле знаний и умений обучающихся. Этот контроль является важным звеном учебного процесса, от правильной постановки которого во многом зависит успех обучения. Применение информационных технологий в образования, в том числе электронных учебников и тестов повышает качество и эффективность не только преподавания, но и контроля знаний.

Компьютерное тестирование позволяет заинтересовать практически всех учащихся, к тому же оно дает возможность преподавателю проверить всех учащихся, затратив при этом минимальное количество времени, что является немаловажным аспектом.

От традиционных оценок и контроля знаний учащихся тесты отличаются объективностью измерения результатов обучения, поскольку они ориентируются не на субъектное мнение преподавателей, а на объектные эмпирические критерии.

Основной целью курсовой работы является разработка теста итогового контроля по теме: "Теория множеств", обработка информации в среде программы MyTestX и дальнейшее ее использование в сфере образования.

Краткие теоретические сведения. Теория множеств.

1.Способы задания множеств.

Понятие множество является первичным и поэтому формально не может быть определено. Под множеством понимается любое собрание определенных и различных между собой объектов, мыслимое как единое целое. В этом интуитивном определении, принадлежащем немецкому математику Г. Кантору, существенно то, что собрание элементов рассматривается как единое целое.

Для удобства и кратности записей используют специальными обозначениями – кванторы. Эти обозначения используются во всех разделах математики. Слово «любой», «всякий», «каждый» будем обозначать с помощь квантора (общности),слова «существует», «найдется», «можно найти» - с помощью (существования).

Множества обозначаются прописными буквами латинского алфавита X,Y…, элементы множеств - строчными буквами x,y… .

Утверждение «Элемент x принадлежит множеству X» записывается следующим образом: ; «Элемент x не принадлежит множеству Y» - .

Множество называется пустым и обозначается , если оно не содержит ни одного элемента.

Множество Y называется подмножеством X, если для следует, что . При этом пишут: , то пишут: . В этом случаеY называется собственным подмножеством X.

Пример 1.1. Рассмотрим цепочку включений множеств

.

Здесь пустое множество содержится во множестве натуральных чисел, которое содержится во множестве целых чисел, которое содержится во множестве рациональных чисел, которое содержится во множестве вещественных чисел, которое содержится во множестве комплексных чисел.

Различают два способа задания множеств: перечислением элементов и описанием свойств элементов.

2.Задание множества перечислением его элементов. Конечное множество можно задать перечислением его элементов и записать в форме: .

Пример 1.2. Рассмотрим множество . Оно состоит из элементов 1,2,3.

В случае бесконечного множества или трудностей с выписыванием элементов конечного множества можно использовать рекурсивное задание множеств, когда множество задается перечисляющей процедурой.

В этом случае множество задается некоторыми начальными элементами и алгоритмом (процедурой) нахождения новых элементов по уже известным.

Пример 1.3. Зададим рекурсивно множество X алгоритмом:

1. ;

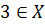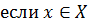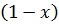2. , то элементы и принадлежат X;

3. других элементов в X нет;

Заметим, что это множество – конечное, и его можно было задать выписыванием его элементов .

Частным случаем рекурсивного задания множества является способ задания, основанный на процедуре, называемой математической индукцией. Рассмотрим его на примере задания множества натуральных чисел.

Пример 1.4. Множество N задается следующими правилами:

1.задается базис индукции(исходный элемент): ;

2.указывается индуктивный переход: если ;

3.устанавливается правило замыкания:

других элементов, кроме построенных в 1 и 2, в N нет.

Множества, которые можно задать перечислением, называются перечислимыми. Но имеются множества, которые задают только описанием свойств их элементов.

3.Задание множества описанием свойств его элементов. Описание свойств элементов обычно задается так: пусть - утверждение , заключающееся в том, что элемент обладает свойством Р. Тогда запись

означает, что рассматривается множество всех элементов , обладающих свойством Р.

Таким способом можно задать как конечные, так и бесконечные множества.

Пример 1.5. Рассмотрим множество натуральных четных чисел. Это можно записывать в следующим образом:

.

Если рассматривать теорию множеств без ограничений на способы задания множеств, то такая теория называется наивной теорией множеств.

Еще при жизни Г.Кантора, создателя наивной теории множеств, были обнаружены многочисленные парадоксы в этой теории.

Приведем одон из известных парадоксов Б.Рассела.

Пусть М – множество всех множеств. Тогда очевидно, что . Тем самым существуют множества, содержащие себя как свой элемент.

Рассмотрим некоторое множество X, которое не содержит себя как свой элемент.

Пусть Y-множество всех таких множеств X, т.е. множество всех множеств, не содержащих себя как свой элемент.

Зададимся вопросом: каково множество Y? Содержит оно себя как элемент или нет? Возможны два случая: 1) содержит; 2)не содержит.

В первом случае .Тогда по определению множества Y имеем . Получили противоречие.

Во втором случае . Тогда по определению множества Y имеем . Получили также противоречие.

Иногда этот парадокс Рассела облекают в бытовую форму. Тогда появляется следующая парадоксальная ситуация. В полку имеется полковой Брадобрей, который руководствуется следующим приказом. Брить бороды только у тех людей, которые сами себя не бреют. Спрашивается, может ли Брадобрей брить себе бороду? Получается так, что если он не бреет себе бороду , то по приказу он должен себя брить. Как только Брадобрей начинает брить себе бороду, то по приказу он не должен себя брить. Парадокс .

Избежать парадоксов удается только в рамках аксиоматической теории множеств, т.е. теории, которая ограничивает способы задания множеств специальной аксиоматикой.