2.3. Типовые примеры решения задач
Пример 2.1. К
зажимам цепи рис.2.5 приложено напряжение
В.
Параметры цепи заданы:
Ом,
Ом,
Ом,
Ом,
Ом,
Ом,
Ом.
О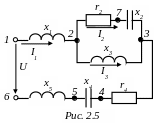
пределить
действующие значения токов во всех
ветвях и напряжений на всех участках,
записать мгновенные значения токов.
Определить также активную, реактивную и полную мощности цепи и построить полную векторную диаграмму напряжений и токов.
Решение
Записываем входное напряжение цепи в комплексной форме
В
(вектор
совпадает с осью вещественных чисел).
Определяем комплекс сопротивления участка цепи между точками 2 и 3
Ом.
Комплекс общего сопротивления цепи
Ом.
Комплекс тока в неразветвленной части цепи определяем по закону Ома
А.
Действующее значение тока
А.
Найдем комплексы токов в параллельных ветвях
А.
Следовательно,
А.
А ,
А.
Активная мощность цепи
Вт.
Реактивная мощность цепи
вар.
Комплекс полной мощности
ВА ,
следовательно,
модуль этой мощности
ВА,
или
ВА.
Мгновенные значения токов
А ,
А ,
А.
Для построения полной векторной диаграммы цепи определяем комплексы падений напряжения на всех ее элементах
В ,
В ,
В ,
В ,
В ,
В ,
В.
П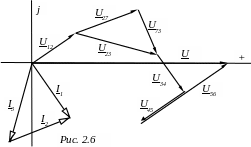
о
результатам расчета построена векторная
диаграмма на комплексной плоскости
(рис.2.6).
Указания.
1. Если мгновенное напряжение имеет
отличную от нуля начальную фазу, например,
,
то комплекс действующего значения
напряжения будет иметь вид
.
2. Задачу 2.1 и пример 2.1 можно решать и методом проводимостей (методом векторных диаграмм).
Пример 2.2.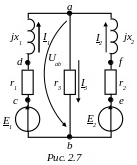 
В
схеме рис.2.7 ЭДС
В, причем
отстает по фазе от
на угол
.
Сопротивления
Ом,
Z3=10 Ом.
Определить токи во всех ветвях. Построить топографическую диаграмму, совмещенную с векторной диаграммой токов.
Решение
Предлагаемая задача может быть решена одним из методов, которые применялись для расчета сложных цепей постоянного тока.
Воспользуемся, например, методом двух узлов.
Если совместим вектор ЭДС с осью вещественных чисел, то комплексы ЭДС будут соответственно равны
В,
В.
Тогда узловое напряжение
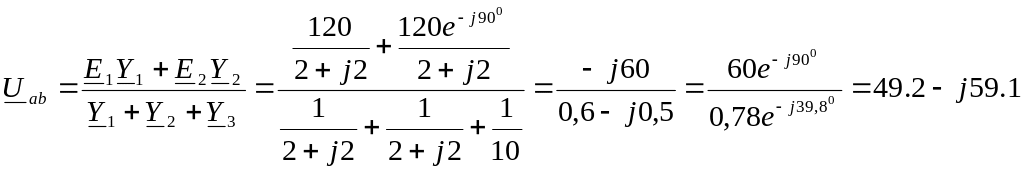В,
а его модуль
В.
Ток первого источника
А ,
А.
Ток второго источника
А ,
А.
Ток третьей ветви
А ,
А.
Приняв потенциал узла b равным нулю, определяем потенциалы других характерных точек
В,
В,
В,
В,
В,
В
и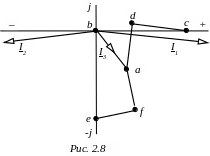
строим топографическую диаграмму цепи,
совмещенную с векторной диаграммой
токов (рис. 2.8).
Пример 2.3. На рис.2.9 изображена схема цепи с индуктивно связанными элементами.
Т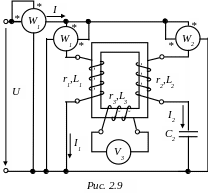
ребуется
рассчитать токи, построить полную
векторную диаграмму, определить показания
ваттметров и вольтметра, а также величину
и направление передачи активной мощности
через индуктивную связь, если
u=300sin(t+45o)
В,
Ом,
Ом,
Ом,
Ом,
Ом.
Решение
На основании исходной схемы (рис.2.9) определяем одноименные зажимы индуктивно связанных элементов (обозначаются «») и переходим к рассмотрению эквивалентной схемы (рис.2.10).
Расчет токов выполним методом уравнений Кирхгофа.
П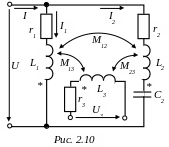
о
законам Кирхгофа имеем
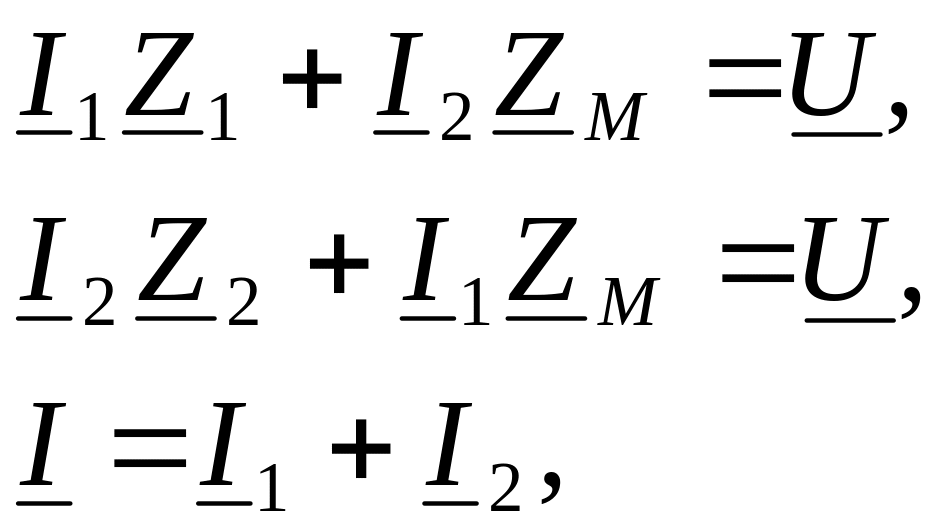
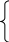(2.1)
где:
B,
Ом ,
Ом ,
Ом.
Следует отметить, что ток
равен нулю, так как вольтметр имеет
большое внутреннее сопротивление,
поэтому влияние этого тока на первый и
второй элементы отсутствует.
Решая систему уравнений (2.1), получим
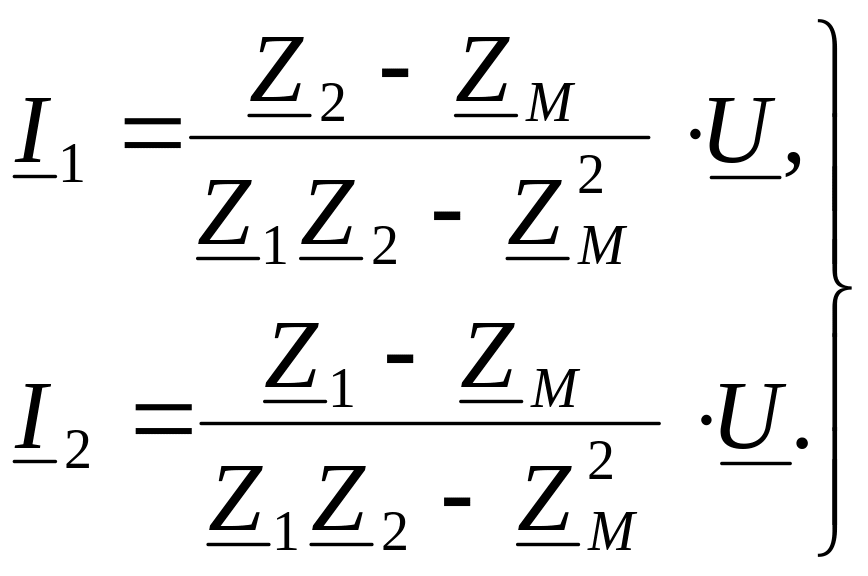(2.2)
Уравнение для определения показания вольтметра составляется по второму закону Кирхгофа
(2.3)
Подставляя числовые значения величин в уравнения (2.2) и (2.3) и учитывая (2.1), находим
А,
А,
А,
В,
В.
Следовательно, вольтметр покажет 158,1 В.
Суммарная активная мощность, потребляемая из сети (показание первого ваттметра):
Вт.
Активная мощность, потребляемая из сети отдельными ветвями (показания двух других ваттметров):
Вт,
Вт.
Баланс мощностей
Вт.
Тепловые потери мощности в первой ветви
Вт.