Основные определения

Мощность теплового потока или просто тепловой поток Q, [Вт] – это количество теплоты, передаваемое в единицу времени через поверхность теплообмена F, [м²].

Интенсивность переноса теплоты характеризуется плотностью теплового потока. Плотность теплового потока – это количество теплоты, передаваемое в единицу времени через единичную площадь поверхности теплообмена, q [Вт/м²].

q = Q / F, Вт/м² (1.1)

Поверхность теплообмена F – это поверхность, через которую происходит передача теплоты. Движущаяся среда (жидкость или газ), используемая для переноса теплоты, называется теплоносителем.

Температурным полем называется совокупность мгновенных значений температуры во всех точках тела или системы тел в данный момент времени. Математическое описание температурного поля имеет вид

t = f(x, y, z, ), (1.2)

где t – температура;

x, y, z – пространственные координаты;

 – время.

Температурное поле, описываемое уравнением (1.2), называется нестационарным, и ему соответствует неустановившийся тепловой режим. В этом случае температуры зависят не только от координат, но и от времени.

В том случае, когда распределение температуры в теле не изменяется со временем, температурное поле называется стационарным и ему соответствует установившийся тепловой режим:

t = f(x, y, z). (1.3)

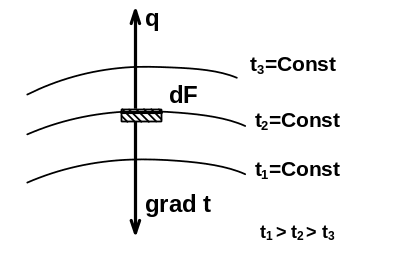
Поверхность, во всех точках которой температура одинакова, называется изотермической. Изотермические поверхности могут быть замкнутыми, но не могут пересекаться. Быстрее всего температура меняется в направлении, перпендикулярном изотермической поверхности. Скорость изменения температуры по нормали к изотермической поверхности характеризуется градиентом температуры (рисунок 1.1).

	Градиент температуры (grad t) – есть вектор, направленный по нормали к изотермической поверхности и численно равный производной от температуры по этому направлению: , К/м, (1.4) где – единичный вектор, направленный в сторону воз-
Рисунок 1.1 - Направление градиента температуры и вектора теплового потока относительно изотермы t2 = Const температурного поля	растания температур нормально к изотермической поверхности. Он показывает только направление.

7 Теплопроводность.

Явление теплопроводности состоит в переносе теплоты микрочастицами (молекулами, атомами, электронами и т.п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур.

Основной закон теплопроводности – закон Фурье:

, Вт/м² (7.1)

где  – коэффициент теплопроводности, Вт/(мК). Он характеризует способность вещества, из которого состоит рассматриваемое тело, проводить теплоту.

grad t – градиент температуры, К/м.

Знак «–» в формуле (7.1) указывает на противоположные направлений вектора теплового потока и вектора градиента температуры. Вектор плотности теплового потока q всегда направлен в сторону наибольшего уменьшения температуры.

Далее будет рассматриваться только стационарный режим теплопроводности.