3.2 Функциональная структура программного комплекса

В данном подразделе приводится рисунок, отображающий функциональную структуру программного комплекса для заданной автоматизированной системы, и дается краткое описание назначения всех модулей программного комплекса. На рисунке модули, подсистемы и пользователь программного комплекса соединяются стрелками, отображающими направления внешних и внутренних потоков данных. Рядом со стрелками наносятся условные обозначения соответствующих параметров объекта, введенные в подразделе 3.1.

Например:

Для решения задачи выбора режимных параметров одношнекового экструдера, обеспечивающих заданную производительность экструдера и качество (степень деструкции) изготавливаемой рукавной пленки, разработан гибкий проблемно-ориентированный программный комплекс, функциональная структура которого представлена на рисунке 4.

Рисунок 4 – Функциональная структура программного комплекса

На рисунке 4 использованы следующие обозначения:

U^min = {N^min, T_b^min} – вектор минимально допустимых по регламенту значений частоты вращения шнека и температуры корпуса экструдера;

U^max = {N^max, T_b^max} – вектор максимально допустимых по регламенту значений частоты вращения шнека и температуры корпуса экструдера;

U = {N, T_b} – вектор шагов варьирования частоты вращения шнека и температуры корпуса экструдера, значения которых выбираются из условия возможности физической реализации управлений на экструдере.

Далее в этом подразделе идет краткое описание подсистем и модулей программного комплекса и того, как пользователь взаимодействует с комплексом (какие данные вводит, какие результаты получает). При этом необходимо расшифровать вновь введенные обозначения параметров, как в указанном выше примере.

3.3 Структура и параметры математической модели для расчета показателей эффективности химико-технологического процесса

Данный подраздел начинается с предложения:

Ядром разработанного программного комплекса является математическая модель химико-технологического процесса, позволяющая рассчитать его критериальные показатели для заданных характеристик перерабатываемого материала, геометрических и режимных параметров технологического оборудования.

Дальнейший текст полностью берется из приложения Б к заданию. В тексте, предваряющем формулы, следует сделать ссылки на литературу по моделированию (Гольцева Л.В. и др. Математическое моделирование химико-технологических процессов – для всех заданий; литература из пункта 4 раздела «Исходные данные к проекту» задания – для заданий по экструзии и термоформованию). При этом в комментариях не нужно расшифровывать те обозначения параметров, которые были расшифрованы в предыдущих подразделах.

3.4 Алгоритм поиска режимных/геометрических параметров объекта, обеспечивающих заданные показатели его эффективности

Например:

Алгоритм поиска частоты вращения шнека и температуры корпуса экструдера, обеспечивающих заданные значения производительности экструдера и индекса термической деструкции рукавной полимерной пленки, представлен на рисунке 5.

Алгоритм включает три этапа. На первом этапе осуществляется ввод задания на исследование процесса экструзии Y₀, содержащего значения геометрических параметров шнека и головки экструдера _E, характеристик полимерного материала H_M, регламентных пороговых ограничений {U^min, U^max} и шагов варьирования U режимных параметров экструдера, предельные значения производительности экструдера G₀ и индекса термодеструкции экструдата I_d^max. На следующем этапе при варьировании частоты вращения шнека и температуры корпуса в заданных диапазонах по аналитической математической модели процесса одношнековой экструзии рассчитываются значения производительности экструдера и индекса термодеструкции экструдированного полимерного материала. Если рассчитанные значения критериальных показателей процесса удовлетворяют заданным ограничениям, то соответствующие значения режимных параметров экструдера сохраняются как допустимые значения режимных параметров. На третьем этапе осуществляется вывод допустимых значений частоты вращения шнека и температуры корпуса и массивов значений производительности экструдера и индекса деструкции экструдата, визуализируемых в виде таблиц и трехмерных графиков, представляющих зависимости критериальных показателей от режимных параметров.

Разработанный алгоритм является настраиваемым на характеристики экструдера и полимерного материала, требования к показателям эффективности процесса экструзии.

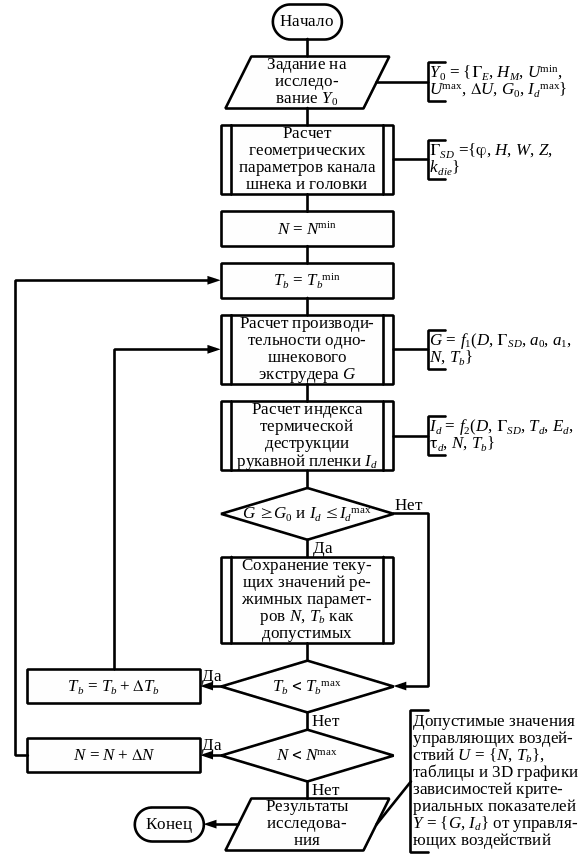
Рисунок 5 – Алгоритм поиска допустимых режимных параметров экструдера