4. Деякі відомості з лінійної алгебри

Мінором k-ого порядку називають визначник, утворений з елементів, що лежать на перетині виділених k рядків і k стовпців визначника n-ого порядку:

Доповнювальним мінором називають визначник (n–k)-ого порядку, який одержуємо в результаті викреслювання з визначника порядку n стовпців і рядків, що утворюють мінор .

Головним називають мінор, утворений з рядків і стовпців з однаковими номерами. Для визначника порядку n існує мінорів порядку m, а всього 2ⁿ мінорів.

Алгебраїчним доповненням мінору k-ого порядку називають величину , де – сума номерів рядків і стовпців, що визначають мінор .

Для побудови оберненої матриці достатньо розв’язати рівняння (оскільки , то матриця , власне, і буде шуканою матрицею ). Ідея полягає в тому, щоб звести матрицю до одиничної при збереженні рівності правої та лівої частин. Робиться це так. Формуємо матрицю з n рядків (n – розмірність квадратної матриці (і , відповідно)) і 2n стовпців, причому перші n стовпців цієї матриці становлять матрицю A, а останні n стовпців – матрицю . Послідовно для кожного натурального числа j від 1 до n (n – розмір квадратної матриці ) виконуємо таку процедуру: 1) ділимо всі елементи j-ого рядка матриці на (в результаті дорівнюватиме 1); 2) множимо одержаний рядок на ( , ) і рядок-результат цього множення додаємо до і-ого рядка (у перетвореній матриці весь стовпець з індексом j містить всі нульові елементи, окрім елемента , що дорівнює 1). За n ітерацій матриця стане одиничною (перші n стовпців матриці утворюватимуть одиничну матрицю). Натомість решта n стовпців матриці являтимуть собою шукану матрицю .

Приклад: Знайти обернену матрицю для .

Сформуємо матрицю розміром 3*6 і виконаємо відповідні перетворення:

Перетворення припиняються, коли перші n перших стовпців матриці утворять одиничну матрицю. Знайдена обернена матриця:

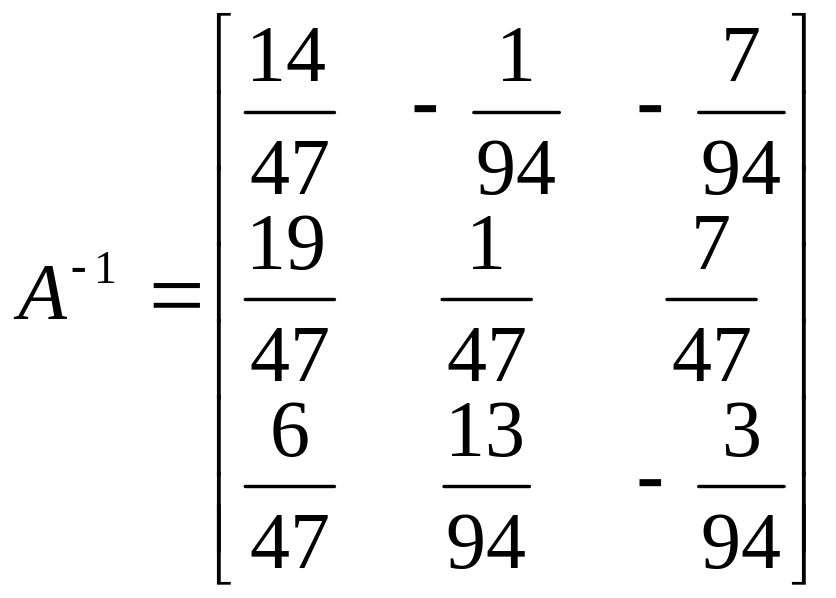
Крім того, обернену матрицю можна обчислити таким чином:

, де , де

матрицю одержуємо шляхом заміни елементів транспонованої матриці їхніми алгебраїчними доповненнями.

Скалярним добутком двох векторів a та b довжини n є число (скаляр), рівний сумі добутків відповідних координат векторів a та b:

Скалярний добуток існує лише для векторів однакової довжини.

Для векторів у просторі часто використовують співвідношення:

,

де φ – кут між векторами a та b, і – довжини векторів a та b. Довжина вектора є коренем з суми квадратів всіх його координат.

Відповідно, косинус кута φ між двома векторами a та b визначають за формулою:

Сам кут між векторами (у радіанах) можна знайти за допомогою функції acos (арккосинус). З відомого співвідношення π рад = 180˚ знаходимо, що 1 радіан дорівнює 180/π градусів, відповідно, n радіан дорівнює n∙180/π градусів.

Векторним добутком двох векторів a та b є вектор:

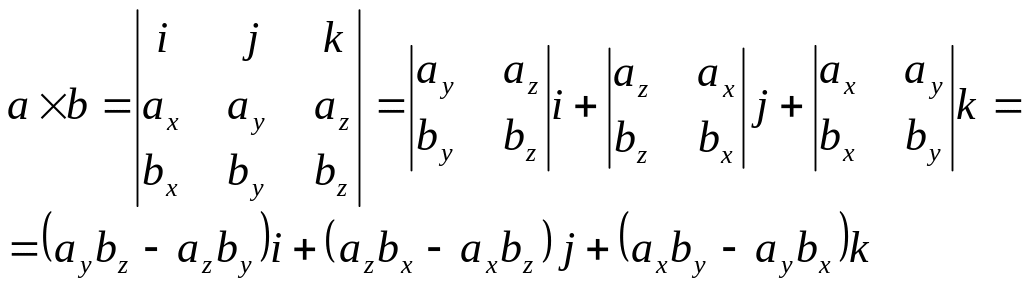
Координатами цього вектора є числа , .

Операція множення визначена лише для двох матриць, узгоджених за формою, тобто, таких, що кількість стовпців першої матриці рівна кількості рядків другої матриці. Добутком матриці А розміром і матриці В розміром є матриця розміром , елементи якої обчислюються за формулою:

З існування добутку АВ, взагалі кажучи, не випливає існування добутку ВА.

Квадратна матриця називається верхньою трикутною, якщо всі елементи, розміщені під головною діагоналлю, дорівнюють 0:

		…
0		…
…	…	…	…
0	0	0

Квадратна матриця називається нижньою трикутною, якщо всі елементи, розміщені над головною діагоналлю, дорівнюють 0:

	0	…	0
		…	0
…	…	…	…
		0

Ранг матриці – це число її незалежних рядків (або стовпців). Якщо ранг матриці рівний r, то принаймні один з її мінорів порядку r є ненульовим, а всі мінори вищих порядків рівні 0. Тобто ранг – це найбільший порядок ненульового мінору матриці.

Кількість лінійно незалежних рівнянь у системі лінійних алгебраїчних рівнянь є рангом системи, тобто, рангом матриці.