Тема 3.3

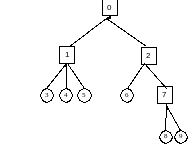
Вправа 3. Намалювати 2-3 дерево, отримане в результаті вставки в пусту множину (представлену як 2-3 дерево) елементів 5, 2, 7, 0, 3, 4, 6, 1, 8, 9.

Розвязання:

Вправа 6. Показати, що алгоритм Дейкстри працює неправильно, якщо ваги дуг можуть бути від’ємними.

Розвязання:

За алгоритмом Дейкстри шлях повинен додаватись, щоб отримати дійсну відстань між двома вершинами на графі, але при наявності дуг відємної довжини потрібно не додавати, а віднімати , саме тоді алгоритм працює неправильно.

Вправа 9. Побудувати алгоритм зчитування арифметичних виразів, які представлені у вигляді ациклічного графу.

Розвязання:

Оскільки арифметичні вирази представлені у вигляді ациклічного графу, отже алгоритм буде у вигляді бінарного дерева.Тоді алгоритм зчитування буде мати розгалуження, де основні команди будуть листками дерева.Тобто спочатку ми йдемо по дереві і перевіряємо чи задовольняються умови лівої ланки, якщо ні-то переходимо на праву, аналогічно з правою, тоді пройшовши далі вглиб дерева, знову на розгалуженні повторюємо заданий алгоритм, який згодом припиниться на тому, що вже із зчитування арифметичних виразів ми перейдемо до виконання інструкцій. Таким чином після виконання інструкцій обробка завершиться, і ми повернемось на початок графу для отримання нового виразу.

Вправа 12. Розглянемо дерево гри, в якому використовуються 6 кульок та гравці 1 і 2 вибирають по черзі від одної до трьох кульок. Гравець, який взяв останню кульку вважається переможцем.

а) скласти повне дерево цієї гри;

б) якщо це дерево переглядати за допомогою методу альфа-бета відсіків, а вузли, які є конфігураціями з найменшою кількістю кульок, переглядати в першу чергу, то які вузли будуть відсічені?

в) хто виграє, якщо обидва гравці будуть діяти оптимальним шляхом?

Розвязання:

Я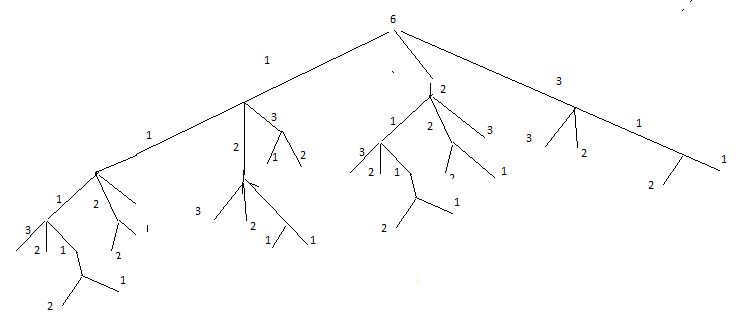 кщо це дерево переглядати за допомогою методу альфа-бета відсіків, а вузли, які є конфігураціями з найменшою кількістю кульок, переглядати в першу чергу, то відсіченими будуть всі інші вузли. На питання «хто виграє, якщо обидва гравці будуть діяти оптимальним шляхом?» можна дати відповідь, пройшовшись по дереві гри по вибору одиничок, і тоді вийде, що виграє перший гравець

Тема 4.1

Вправа 3. Які з граматик, наведених у вправі 1, породжують регулярну мову.

Розвязання:

Автоматні граматики. Правила виведення мають вигляд:

d_i  d_j або d_i  , де d_i, d_j  D,  - слово в алфавіті Е.

Отже,граматики 1) та 2) – породжують регулярну мову.

Вправа 6. Навести приклади ланцюжків, які породжуються граматиками вправи 1.

Розвязання:

Отже, візьмемо для прикладу такі 3 граматики із вправи 1:

1) d₀  010 d₁, 2) d₀  010 d₀,

d₁  0 d₁, d₀  Є,

d₁  Є,

6)d₀  1 d₁ 1,

d₁  1 d₁ 1,

1 d₁ 1  1 0 1.

Побудуємо до них ланцюжки:

1){010001,01000011,0100000111…};

2){01001,0100011,010000111,…};

3){11011,11100111,11110001111};

Вправа 9. Задати граматику G, що породжує мову

L(G) = {A, AAБ, AAAББ,...}.

Розвязання:

G= <{d₀ , d₁}, {A, Б}, P, d₀ > дe множина Р містить правила

d₀  Ad₁ , d₁  AБ;

Вправа 12. Які з граматик, наведених у вправі 6 теми 1.2, породжують контекстно-вільну мову?

Розвязання:

Правила виведення мають вигляд:

d_i , де d_i  D,  - слово в алфавіті DE.

Контекстно-вільна граматика це четвірка із множини нетермінальних символів, множини термінальних символів та множини правил та початкового символу. Тобто будемо обирати такі, які будуть задавольняти наші умови, до них належать всі із цієї вправи.

Вправа 15. Задати граматику, що породжує такі мови:

1. L = {010, 00100, 0001000,…}

G= <{d₀ , d₁}, {1, 0}, P, d₀ >

d₁d₀1d₀

d₀0;

2. L = {1001, 110011, 11100111, …}

G= <{d₀ , d₁}, {1, 0}, P, d₀ >

d₁d₀00d₀

d₀1;

3. L = {01010, 0110110, 011101110,…}

G= <{d₀ , d₁}, {1, 0}, P, d₁ >

d₁0d₀0d₀0

d₀1;

4. L = {АБВ, ААБВВ, АААБВВВ, …}

G= <{d₀ , d₁,d₂}, {A, Б,В}, P, d₀ >

d₀  d₁Бd₂, d₁  A; d₂ В;

5. L = {АБВ, АББВВ, АБББВВВ, ...}

G= <{d₀ , d₁,d₂}, {A, Б,В}, P, d₀ >

d₀ A d₁d₂, d₁  Б; d₂ В;

6. L = {АБВ, ААББВ, АААБББВ, ...}

G= <{d₀ , d₁,d₂}, {A, Б,В}, P, d₀ >

d₀ d₁d₂В, d₁  А; d₂ Б;

Вправа 18. Установити порожнечу або непорожнечу мов, що породжуються такими граматиками:

І) G₁ = <{d₀ , d₁, d₂, d₃ , d₄, d₅}, {0, 1, 2, 3}, P, d₀ > ,

де Р містить правила

d₀  d₁d₂ , d₂  1d₀ , d₄  2d₅ 2,

d₁ 0d₁ , d₃  2d₃ d₄ , d₅  3d₃ 3,

d₁  1, d₃  2d₅ , d₅  2;

2) G₂ = <{d₀ , d₁, d₂}, {0, 1, 2, 3}, P, d₀ > ,

де P містить правила

d₀  0d₁d₂ , d₂  2d₂2 ,

d₁  1d₀ , d₂  Є ;

3) G₃ = <{d₀ , d₁, d₂}, {0, 1, 2, 3}, P, d₀ > ,

де P містить правила

d₀  0d₁0 , d₁  3 ,

d₁  1d₁2 , d₂  Є ;

4) G₄ = <{d₀ , d₁, d₂, d₃}, {0, 1, 2, 3}, P, d₀ > ,

де P містить правила

d₀  1 , d₁  0d₁2 , d₃  1 d₃,

d₀  0d₁2 , d ₁ 1 , d₃  Є ;

d₂  3d₃ ,

5) G₅ = <{d₀ , d₁, d₂}, {0, 1, 2, 3}, P, d₀ > ,

де P містить правила

d₀  0 d₀ 1 d₁, d₁  2 ,

d₀  Є , d₂  3 .

Розвязання:

1)некорисні символи d₂таd₄;

2) d₁;

3) d₂ кінець слова неможливо досягнути;

4) (d₂ та d_3), кінець слова не можна досягнути;

5) некорисні символи d₁таd_2.

Вправа 21. Перетворити граматики вправи 18 до вигляду, вільного від некорисних та недосяжних символів.

Розвязання:

І) G₁= <{d₀ , d₁, d₃ , d₄,d₅}, {0, 1, 2, 3}, P, d₀ > ,

де Р містить правила

d₀  d₁d₂ , d₂  1d₀ , d₄  2d₅ 2,

d₁ 0d₁ , d₃  2d₃ d₄ , d₅  3d₃ 3,

d₁  1, d₃  2d₅ , d₅  2;

2) G₂= <{d₀ , d₁}, {0, 1, 2, 3}, P, d₀ > ,

де P містить правила

d₀  0d₁d₂ ,

d₁  1d₀ ,

3) G₃= <{d₀ , d₁}, {0, 1, 2, 3}, P, d₀ > ,

де P містить правила

d₀  0d₁0,

d₁  3,

d₁  1d₁2

4) G₄= <{d₀ , d₁, d₃}, {0, 1, 2, 3}, P, d₀ > ,

де P містить правила

d₀  1, d₁  0d₁2, d₃  1d₃,

d₀  0d₁2, d ₁ 1, d₃  Є;

d₂  3d₃ ,

5) G₅= <{d₀ , d₁, d₂}, {0, 1, 2, 3}, P, d₀ > ,

де P містить правила

d₀  0 d₀ 1d₁,

d₁  2,

d₀  Є,

Вправа 24. Чи можуть бути у граматиці побудовані різні дерева виводу для якого-небудь ланцюжка? Якщо відповідь позитивна, тоді навести приклад такої граматики і не менш ніж двох різних дерев виводу для цього ланцюжка.

Розвязання:

Так можуть.

Наприклад ланцюжок {0, 001, 00011,0000111...}можна описати граматикою

G = (D,E, {g},P,d₀) з правилами Р:

d₀ d₁0d₂,

d₁g 0d₁,

d₂g d₂ 1

d₁εd₂ε

Або G = <{d₀,d₁}, {0,1}, P, d₀ > з правилами Р:

d₀ 0 d₁, d₁ 0 d₁1, d₁ε

Вправа 27. Задати граматики, що породжують такi мови:

І/ L(G) = {АБВВ, ААББВВВ, АААБББВВВВ,... }

2/ L(G) = {ААБВ, АААББВВ, AAAAБББВВВ, ...}

З/ L(G) = {АББВ, ААБББВВ, АААББББВВВ....}

4/ L(G) = {А, ААБ, АААББВ, ААААБББВВ,...}

5/ L(G) = {В, БВВ, АББВВВ, ААБББВВВВ,...}

6/ L(G) = {Б, АББ, ААБББВ, АААББББВВ,... }

Розвязання:

1) G= <{d₀ , d₁}, {A, Б,В}, P, d₀ >

d₀  d₁В, d₁  A,Б,В;

2) G= <{d₀ , d₁}, {A, Б,В}, P, d₀ >

d₀  Аd₁, d₁  A,Б,В;

3) G= <{d₀ , d_1,d₂}, {A, Б,В}, P, d₀ >

d₀  d₁Бd₂, d₁  A,Б; d₂В;

5) L(G) = {В, БВВ, АББВВВ, ААБББВВВВ,...}

G = <{d₀ , d_1, d_2, d₃ }, {А, Б, В}, P, d₀ > ,

d₀ d₁ В

d₁ d₂ Б d₁ В

d₂ А d₂

d₁ ε,

6) L(G) = {Б, АББ, ААБББВ, АААББББВВ,... }

G = <{d₀ , d_1, d_2, d₃ }, {А, Б, В}, P, d₀ > ,

d₀ d₁ Б d₂

d₁ А d₁

d₂ Б d₂ В

d₂ Б d₂

d₁ ε,

d₂ε

Вправа 30. Задати індексну граматику, що породжує мову з вправи 27.

Розвязання:

Індексна граматика має вигляд G = ({d₀,d₁,d₂,d₃,d₄}, {0,1}, {f, g},P,d₀), де множина Р містить такі правила, тоді запишемо одну із них таким способом:

G = ({d₀,d₁,d₂,d₃ }, {А,Б,В}, { },P,d₀), де множина Р містить такі правила:

d₀→d₁А

d₁→d₂d₃

d₂→

Вправа 33. Навести приклади слів, що породжуються програмною граматикою:

G = <{d₀ , d₁ , d₂ , d₃ }, {А, Б, В, Г}, {1, 2, 3,…,8}, P, d₀ >,

де Р містить такі правила виводу:

І/ d₀  d₁ d₂ d₃ {2, 5 } 

2/ d₁  A d₁ {3 } 

3/ d₂  Б Б d₂ {4 } 

4/ d₃  В В В d₃ {2, 5 } 

5/ d₁  Г {6 } 

6/ d₂  Г {7 } 

7/ d₃  Г {8 } 

8/ d₀  d₀  

Розвязання:

АББВВВ;

АГББГВВВВВВГ;

АББВВВГВВВ.

Вправа 36. Навести граматику, що породжує мову L = {0, 00, 000,…}, перше слово якої містить символ 0, а всі наступні отримуються з попереднього приєднанням до нього чергового натурального числа символів 0.

Розвязання:

G<{S},{0},{S0,S0 S },S>.