Міністерство освіти і науки, молоді та спорту України

Національний технічний університет України

«Київський політехнічний інститут»

Факультет інформатики та обчислювальної техніки

Кафедра управління та автоматики у технічних системах

Контрольна робота №2

З дисципліни «Основи дискретної математики»

Виконав

Студент групи ІА-21

Гуцол Б.В.

Перевірив

Дорогий Я.Ю

Київ-2012

Тема 3.1

Вправа 2. Графи G₁ та G₂ задані матрицями інцидентності A₁ та A₂:

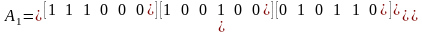
Розвязання:

Необхідно задати геометричним способом графи, отримані:

1) перетином заданих графів:

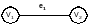
2) об’єднанням заданих графів:

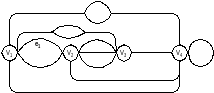
3) усуненням першої вершини графа G₁:

4) усуненням першого ребра графа G₂:

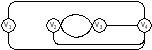
5) замиканням першої та другої вершини графа G₁:

6) стягуванням першого ребра графа G₂:

Стягування ребра графа — заміна кінців ребра однією вершиною, сусідами нової вершини становляться сусіди цих кінців. Граф   можна стягнути до  , якщо другий можна отримати послідовним стягуванням ребер першого.

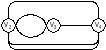
Вправа 5. Як за матрицею інцидентності графа визначити, що в ньому є цикли довжиною 1, 2, 3, ...?

Розвязання:

Цикл – замкнутий ланцюг. потрібно,Отже скільки 1 повторюється в рядку матриця, стільки ця вершина має циклів, скільки разів 1 повторюється 1 в стовпці матриці, така довжина циклу.

Вправа 8. Навести приклад простого графа та побудувати граф, який є доповненням до простого графа.

Розвязання:

Граф, що не містить петлі і паралельні ребра, будемо називати простим.

Граф = (V, E^′, Θ′^΄) назвемо доповненням простого графа G = (V, E, Θ), якщо ребро (v_i,v_j) міститься в множині E^′ у тому і тільки в тому випадку, якщо воно не міс­титься в множині Е.

Задамо граф і його доповнення.

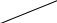
V 1 V2 V2 V4

V3 V4 V1 V3

Граф G Доповнення

Вправа 11. Навести приклад к-часткового графу (к = 3, 4, 5). Побудувати матрицю суміжності цього графу. Які особливості мають матриці суміжності цього графу? Які особливості мають матриці суміжності к-часткових графів?

Розвязання:

Вправа 14. Які особливості мають матриці інцидентності та суміжності графів, що задані геометричним способом симетричними фігурами?

Розвязання:

Матриці інцидентності та суміжності мають такі особливості як: про наявність петель у графі говорять одиниці на головній діагоналі матриці суміжності, а матриця суміжності повного графа складається, за винятком нульової головної діагоналі, тільки з одиниць.Але при використанні матриць суміжності, на відміну від матриць інцидент­нос­ті, втрачається інформація про те, з якими вершинами зв'язані ребра.

Вправа 17. Нехай G_s - множина усіх підграфів графа G=( \/,E,θ ). Необхідно:

а/ перевірити замкненість операцій перетину та об’єднання на G_s :

Через те, що множина G_s являє собою підмножину підграфів графа G, тобто V_S є підмножиною множини V, E_S є підмножиною множини E, θ_S є підмножиною множини θ, то розглянемо дію цих операцій на ці підмножини. Всі отримані підмножини є підмножинами або множиною графа G. Отже ці операції є замкненими на G, бо ми не можемо отримати нових вершин, ребер, або відношень.

б/ якщо < G_s , ∩ , U > ~ алгебраїчна система, то визначити її тип та властивості операцій.

Розвязання:

Тип алгебраїчної системи: <0,1,2,3,4,…,max(V_S+E_S); 0,1,2,3,4,…,max(V_S+E_S)>

∩ - має властивості ідемподентності, комутативності, ассоціативності, доповнення, виділених елементів;

U - має властивості ідемподентності, комутативності, ассоціативності, доповнення, виділених елементів.

Вправа 20. Побудувати кілька дерев графа, заданого у вправі 4.

Розвязання:

Деревом графа G назвемо зв'язний ациклічний підграф графа G.

Варіант 1. G₁= < V₁, E₁, Θ₁ > V₁ ={v₁, v₂, v₃, v₄};

E₁={e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉, e₁₀};

Θ₁(e₁) = (v₁, v₁), Θ₁(e₂) = (v₁, v₃) ,Θ₁(e₃) = (v₁, v₂), Θ₁(e₄) = (v₂, v₂),

Θ₁(e₅) = (v₂, v₄), Θ₁(e₆) = (v₃, v₂) ,Θ₁(e₇) = (v₃, v₃), Θ₁(e₈) = (v₃, v₄),

Θ₁(e₉) = (v₄, v₂), Θ₁(e₁₀) = (v₄, v₃) .

Дерева:

Θ₁(e₂) = (v₁, v₃) ,Θ₁(e₃) = (v₁, v₂), Θ₁(e₅) = (v₂, v₄);

Θ₂(e₂) = (v₁, v₃), Θ₂(e₆) = (v₃, v₂) , Θ₂(e₅) = (v₂, v₄);

Θ₃(e₃) = (v₁, v₂), Θ₃(e₅) = (v₂, v₄), Θ₃(e₈) = (v₃, v₄);

Вправа 23. Користуючись інформацією про точки зчленування графа, як спростити визначення кількості шляхів між кожною парою його вершин?

Розвязання:

Якщо вершини суміжні і їхні пари повторюються кілька разів, то ця кількість і буде кількість шляхів між кожною парою вершин цього графа.

Вправа 26. Навести приклад кореневого дерева. Задати наведене дерево за допомогою дужкового запису.

V0

V2 V1

V3 V4 V5

V6

v₀=(v₁ (v₅ (V₆)), v₂ (v₃,v₄)).

Вправа 29. Навести приклад орієнтованих ейлеревих та гамільтонових графів.

Розвязання:

З в'язний орграф, що містить орієнтований ейлерів ланцюг, називаэться ейлеровим орграфом.

Орієнтованим гамільтоновим графом називаэться орграф, що містить гамільтонів орцикл.

Вправа 32. Описати алгоритм виконання операцій перетину орграфів, які задані матрицею інцидентності.

Розвязання:

Орграф G = (V, E, Θ) назвемо перетином G₁  G₂ орграфів G₁ і G₂, якщо V = V₁  V₂, E = E₁ E₂, а функція Θ визначена для e_i  E і дорівнює Θ₁ чи Θ₂ тільки тоді, коли e_i належить E₁ і E₂, а значення функцій Θ₁ і Θ₂ для аргументу e_i дорівнює парі (v_k, v_l), що належить V₁ і V₂.

Вправа 35. Теоретично обґрунтувати можливість або неможливість розв’язання такої розважальної математичної задачі: задано фігуру, чи можна намалювати цю фігуру, не віднімаючи пера від паперу більше двох разів і не перетинаючи більше одного разу жодну лінію?

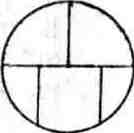
Розвязання:

Неможливо, тому що дозволено зробити два віднімання пера від паперу, а Ейлерів та Гамільтоновий орграф передбачає виконання циклу.

Вправа 38. Як треба модифікувати алгоритм знаходження максимального потоку, щоб використати специфічний вигляд орграфа мережі варіанта З вправи 37?

Розвязання:

Ми можемо використати алгоритм Форда — Фалкерсона, ідея якого така: початково величені потока присвоюється значення 0 :  для всіх .Потім величена потоку ітеративно зростає впродовж пошуку найбільшого шляху.І процес повторюється поки можна знайти найбільший шлях.

Вправа 41. Алгоритм знаходження максимального потоку для мережі з кількома стоками і витоками можна не модифікувати, якщо модифікувати саму мережу. В чому повинна полягати модифікація мережі?

Розвязання:

Модифікація полягає в тому, щоб розташувати суміжні ребра так, щоб серед них можна було вибрати найбільший шлях.

Вправа 44. Вказати перевагу відомих методів знаходження максимального потоку відносно методу повного перебору розрізів, що витікає із теореми Форда - Фалкерсона.

Розвязання:

Перевагою відомих методів знаходження максимального потоку відносно методу повного перебору розрізів, що витікає із теореми Форда – Фалкерсона є те, що в них проста логіка, хороше підлаштування отриманих результатів та простота корегування розв’язань при зміні результатів.