8. На интервале (0,1) наудачу берутся три точки , , . Требуется определить вероятность того, что скалярное произведение вектора на вектор будет меньше единицы.

9. Для данного баскетболиста вероятность забросить мяч в корзину равна 0,7. Проведено 10 бросков. Что вероятнее: он забросит мяч в корзину 6 или 8 раз?

10. Вероятность госпитализации пациента при эпидемии грипп равна 0,002. Найти вероятность того, что из 2000 заболевших поликлиника направит на госпитализацию не более 5 пациентов.

11. Вероятность того, что после одного учебного года учебник уже нельзя будет использовать в дальнейшем, равна 0,25. Найти вероятность того, что придётся закупить не более 1050 новых учебников, чтобы к новому учебному году в библиотеке вуза их снова было 4000.

12. В лотерее 200 билетов, из них 10 - выигрышные. Куплено два билета. Дискретная случайная величина - число выигрышных билетов среди купленных. Найти закон распределения, числовые характеристики, функцию распределе­ния и построить её график.

13. Функция распределения непрерывной случайной величины задана следующим образом:

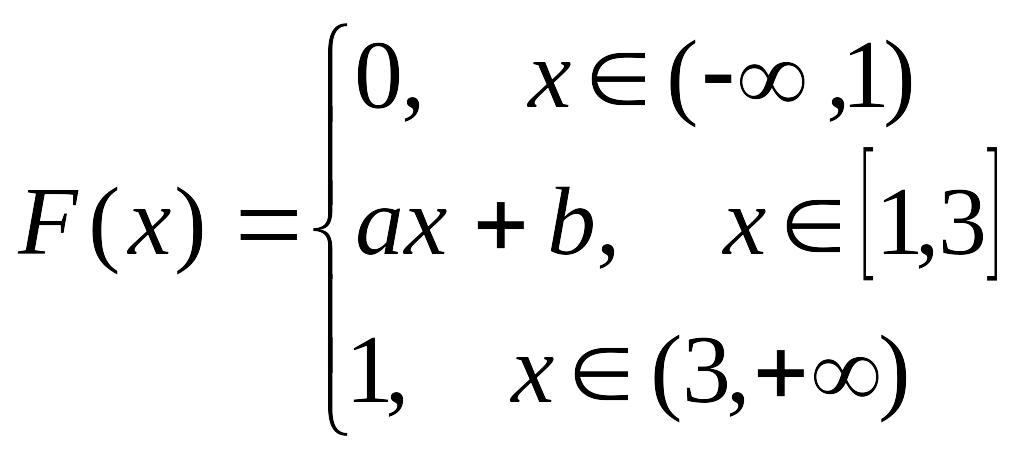
Определить параметры а и b, найти плотность вероятности, числовые характеристики и вероятность попадания случайной величины в интервал [2, 3]. Построить графики р(x) и F(x).

10. Длина куска обоев в рулоне - случайная величина, распределённая по нормальному закону с математическим ожиданием 18 м и среднеквадратическим отклонением 0,3 м. Найти вероятность того, что длина куска в случайно выбранном рулоне обоев будет не меньше 17,5 м.

Вариант 6.

1. В пакете находятся фрукты: 8 яблок и 10 груш. Из пакета случайным образом извлекают 6 фруктов. Какова вероятность того, что среди них 3 яблока и 3 груши?

2. Шахразада получила в подарок от царя Шахрияра 8 золотых колец и 5 шкатулок. Шахразада разместила наудачу кольца в шкатул­ках. Какова вероятность того, что в одной из шкатулок оказались три кольна, а в другой — пять?

3. У Буратино имеется связка из шести золотых ключиков, двумя из которых можно открыть потайную дверцу. Буратино берет наудачу один из ключиков и пытается с его помощью открыть указанную дверцу. Какова вероятность того, что Буратино откроет дверцу ровно с третьей попытки, если после каждой неудачной попытки соответствующий клю­чик: а) откладывается в сторону; б) возвращается в связку?

4. Володя и Вадик стреляют картошкой в живую шляпу. Володя попадает с вероятностью 0,5, Вадик — с вероятностью 0,4. Каждый делает по два выстрела. Какова вероятность того, что при этом будет ровно одно попадание?

5. Во время прогулки Незнайка может с равной вероятностью встретить Молчуна или Ворчуна. При встрече Ворчун с вероятностью 0,9 ворчит и с вероятностью 0,1 молчит; Молчун с вероятностью 0,1 ворчит и с вероятностью 0.9 молчит. Известно, что встретившийся Не­знайке коротышка ворчал. Какова апостериорная вероятность того, что Незнайка встретил Ворчуна?

6. Отправляясь в Африку, доктор Айболит захватил с собой де­сять ящиков: три ящика с градусниками, четыре с гоголем-моголем и три ящика с шоколадками. В пути один ящик был утерян. Прибыв на место, Айболит открывает первый попавшийся ящик. Какова вероят­ность того, что в нем находятся градусники?

7. На интервале (0,1) наудачу берутся две точки и . Какова вероятность того, что выполняется соотношение ?