8. На интервале (0,1) наудачу берутся три точки , , . Требуется определить вероятность того, что скалярное произведение вектора на вектор будет меньше единицы.

9. В магазин вошли восемь покупателей. Найти вероятность того, что трое из них совершат покупки, если вероятность совершить покупку для каждого равна 0,3.

10. Телефонный кабель состоит из 400 жил. С какой вероятностью этим кабелем можно подключить к телефонной сети 395 абонентов, если для подключения каждого абонента нужна одна жила, а вероятность того, что она повреждена, равна 0,0125?

11. К магистральному водопроводу подключены 160 предприятий, каждое из которых с вероятностью 0,7 в данный момент времени осуществляет отбор воды. Найти вероятность того, что в этот момент забор воды производят не менее 80 и не более 120 предприятий.

12. Стрелок имеет три патрона. Вероятность попадания в мишень при каждом выстреле равна 0,8. При попадании в мишень стрельба прекращается. Дискретная случайная величина - число израсходованных патронов. Найти закон распределения, числовые характеристики, функцию распределения и построить её график.

13. Функция распределения непрерывной случайной величины задана следующим образом:

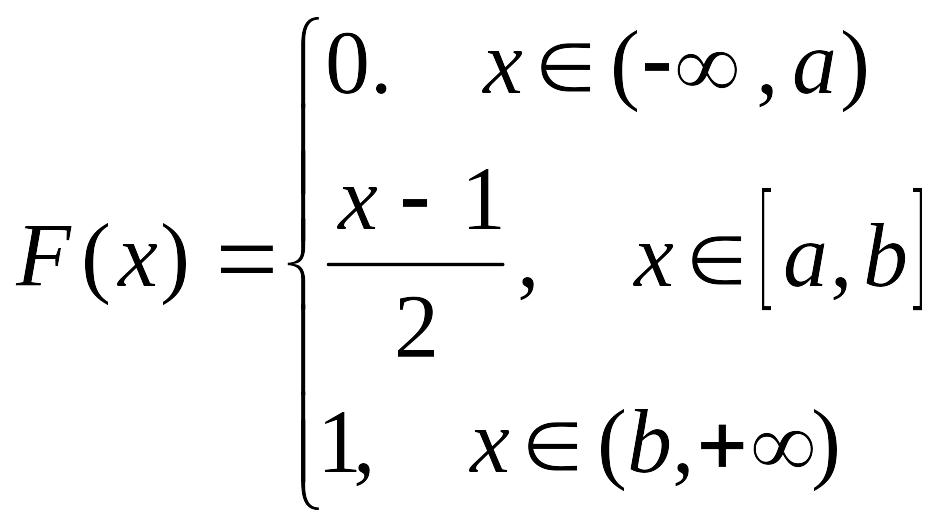
Определить параметры а и b, найти плотность вероятности, числовые характеристики и вероятность попадания случайной величины в интервал [-1, 2]. Построить графики р(x) и F(x).

10. Ошибка взвешивания - случайная величина, распределённая по нормальному закону с математическим ожиданием равным нулю и среднеквадратическим отклонением равным 5 г. Найти вероятность того, что взвешивание проведено с ошибкой, не превышающей по модулю 10 г.

Вариант 4.

1. В лифт восьмиэтажного дома вошли 10 человек, каждый из которых выходит с равной вероятностью на любом этаже, начиная со второго. Какова вероятность того, что на каком-то одном этаже выйдут 6 пассажиров, а на другом — четыре?

2. На столе перед голодным Торопыжкой стоят 10 закрытых ко­робок; в шести из них находятся холодные утюги, в остальных — пря­ники (по одному предмету в каждой коробке). Торопыжка открывает наудачу 3 коробки. Какова вероятность того, что он обнаружит ровно два пряника?

3. Незнайка хочет получить права на вождение газированного автомобиля. На экзамене предлагаются три вопроса и по четыре вари­анта ответа на каждый из них, среди которых лишь один правильный. Экзамен считается сданным, если указаны правильные ответы не ме­нее чем на два вопроса. Незнайка выбирает ответы на вопросы наудачу. Какова вероятность того, что Незнайка сдаст экзамен?

4. Некоторое устройство состоит из четырех блоков, причем на­ дежности (т.е. вероятность безотказной работы в течение какого-то про­межутка времени Т) этих блоков равны р1 = 0,8,p2 = 0,7,р3 = 0.9, р4 = 0, 5. Какова вероятность того, что за промежуток времени Т отка­жет ровно один блок?

5. Отплясывать на поляне могут с равной вероятностью слониха-щеголиха, гиппопотам или носорог. При этом в зависимости от того, кто именно будет отплясывать на поляне, румяная луна может упасть на бедного слона с вероятностями соответственно р1=0,7,р2=0,1,р3 = 0,05. Известно, что луна упала. Какова апостериорная вероятность того, что на поляне отплясывала слониха-щеголиха?

6. Курочка Ряба несет вперемешку простые и золотые яйца. Дед помещает снесенные яйца на одну из двух полок. Через некоторое время выяснилось, что на первой полке 5 простых и б золотых яиц, на второй — соответственно 3 и 7. В ту же ночь случилась беда: по первой пол­ке бежала мышка, хвостиком махнула, одно яичко упало и разбилось. Утром Дед, ничего не зная о случившемся, подошел наудачу к одной из полок и взял первое попавшееся яйцо. Какова вероятность того, что это яйцо — золотое?

7. На интервале (0,1) наудачу берутся две точки и . Какова вероятность того, что выполняется соотношение ?