5.3. Структурный синтез дискретного автомата.
Структурный синтез начинается с кодирования входного и выходного алфавитов и состояний автоматов.
Количество разрядов для входных, выходных сигналов и состояний определяется в соответствие с формулой:
, (6)
где М - мощность множества соответствующего алфавита, ]х[ - означает минимальное целое, не меньшее числа х.
Для
автомата Мура:
,
,
.
Кодирование входных и выходных сигналов автоматов представлено в таблице 5.
Таблица 5 – Кодирование входных и выходных алфавитов
Входные сигналы X |
Коды |
Выходные сигналы Мура Y |
Коды |
|||||||||
a2 |
a1 |
a0 |
d2 |
d1 |
d0 |
|||||||
x0 |
0 |
0 |
0 |
y * |
0 |
0 |
0 |
|||||
x1 |
0 |
0 |
1 |
y0 |
0 |
0 |
1 |
|||||
x2 |
0 |
1 |
0 |
y1 |
0 |
1 |
0 |
|||||
x3 |
0 |
1 |
1 |
y2 |
0 |
1 |
1 |
|||||
x4 |
1 |
0 |
0 |
y3 |
1 |
0 |
0 |
|||||
Один из возможных вариантов кодирования состояний автомата Мура представлен в таблице 6. Для кодирования автомата в соответствии с табл. 6 требуется три триггера.
Таблица 6 – Кодирование состояний автомата Мура
Состояния автомата Мура Q |
Коды |
||
q2 |
q1 |
q0 |
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
5 |
0 |
0 |
1 |
2 |
0 |
1 |
1 |
6 |
1 |
1 |
1 |
3 |
1 |
0 |
1 |
4 |
1 |
0 |
0 |
Однако
вторичный граф автомата Мура (рис.3) не
обеспечивает получение единичного
кодового расстояния между кодами смежных
узлов графа автомата, т.к. число узлов
в цикле должно быть четным. В нашем же
случае, при смене состояний автомата
возможны логические состязания элементов
памяти. Для исключения нежелательных
проявления состязаний элементов и для
обеспечения единичного кодового
расстояния между смежными вершинами
графа в соответствии с рисунком 3 введем
три промежуточных неустойчивых состояния:
для перехода
,
для перехода
и
для перехода
,
как
это показано на рисунке 4.
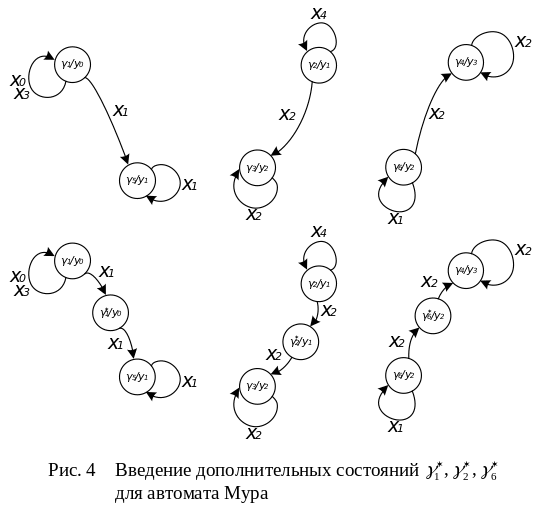
Таблица 7 – Кодирование состояний автомата Мура
Состояния автомата Мура Q |
Коды |
|||
q3 |
q2 |
q1 |
q0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
3 |
0 |
1 |
0 |
0 |
4 |
0 |
0 |
1 |
1 |
5 |
0 |
1 |
0 |
1 |
6 |
1 |
0 |
1 |
0 |
|
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
Для кодирования автомата в соответствии с табл. 7 требуется четыре триггера.
Структурный граф автомата Мура представлен на рис. 5. Все смежные вершины графа обозначены кодовыми комбинациями с кодовым расстоянием, равным единице.
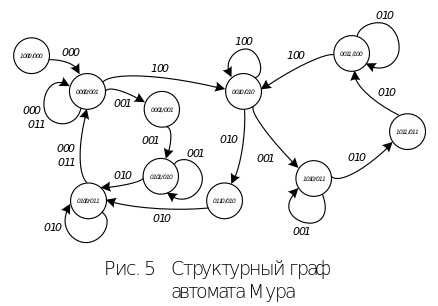
Таблица 8 является структурной таблицой переходов-выходов автомата Мура.