1.2.1 Нечіткі числа (l-r) типу

При вирішенні задач математичного моделювання нечітких систем можна використовувати нечіткі числа (L – R) типу, які передбачають більш просту інтерпретацію розширених бінарних відносин.

Нечіткі числа (L - R) типу - це різновид нечітких чисел спеціального виду, тобто задаються за певними правилами з метою зниження обсягу обчислень при операціях над ними.

Функції приналежності нечітких чисел (L - R) типу задаються за допомогою незрастаючих на множині невід'ємних дійсних чисел функцій дійсного змінного і , що задовольняють властивостям:

а) ;

б)

Толерантне нечітке число задається, відповідно, четвіркою параметрів , де - границі толерантності, тобто в проміжку [ ]значення функції приналежності дорівнює 1.

Толерантні нечіткі числа (L-R)-типу називають трапезоїдними числами. Якщо ми оцінюємо параметр якісно, ​​наприклад, кажучи: "Це значення параметра є середнім", необхідно ввести уточнююче висловлювання типу "Середнє значення - це приблизно від a до b", яке є предмеом експертної оцінки (нечіткої класифікації), і тоді можна використовувати для моделювання нечітких класифікацій трапезоїдного числа[2].

Нечітким числом (L-R) типу називають нечітку величину , у якої функція приналежності визначається наступним чином:

(1.1)

де

Параметр a називають модою або чітким значенням нечіткого числа. Параметри α та β характеризують ступінь розмитості чіткого числа.

Приклади графіків функцій приналежності нечітких чисел (L-R) - типу наведено на рисунку 1.1.

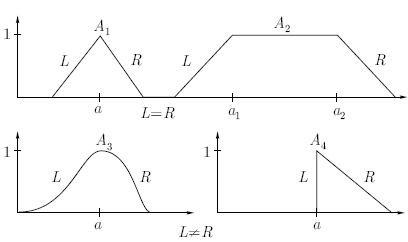
Рисунок 1.1 – Графіки функцій приналежності нечітких чисел (L-R) – типу

Розглянемо далі операції складання, віднімання, множення та ділення з нечіткими числами (L – R) типу. Нехай довільні нечіткі числа (L-R) типу та задані наступним чином:

Операція додавання визначається наступним чином:

,

де параметри результату складання дорівнюють:

Операція віднімання нечітких чисел (L-R) типу визначаються так:

,

где

Операція множення визначається в залежності від знаку співмножників. При множенні додатних нечітких чисел (L-R) типу ,

де

При множенні нечітких чисел (L-R) типу з різними знаками

При множенні нечітких чисел (L-R) типу, для яких модальні значення від’ємні

Операція ділення додатних нечітких чисел (L-R) типу визначаються так:

, де параметри результату ділення дорівнюють:

Унімодальне нечіткі числа (L - R) типу називають трикутними числами. Трикутні числа формалізують висловлювання типу "приблизно дорівнює a ", , причому в міру спадання до нуля ступінь впевненості в оцінці зростає до одиниці.

Трикутне нечітке число А називається трійка дійсних чисел, через які його функція приналежності представлена трикутною функцією виду:

(1.2)

Де - числові параметри, які приймають довільні дійсні значення, при цьому , - модальне значення, - лівий та правий коефіцієнти нечіткості.

Для трикутних нечітких чисел справедливі приведені вище правила виконання операцій додавання, віднімання, ділення, множення нечітких чисел (L - R) типу. Для того, щоб використовувати ці правила слід перейти від виду (1.2) до (1.1)[3].