10. Синтез коректууючих пристроїв методом лах

Корегування систем автоматичного керування проводиться шляхом введення до складу системи додаткових коректуючих ланок. Коректуючі ланки можуть включатися послідовно, паралельно та у вигляді місцевого зворотного зв’язку. Одним з найефективніших інженерних методів синтезу систем автоматичного керування є метод, в основу якого покладено використання логарифмічних амплітудно-частотних характеристик (ЛАХ ) розімкнутої системи. Ідея методу ґрунтується на тому, що для стійких мінімально-фазових систем існує однозначний зв'язок між перехідною характеристикою замкнутої системи і виглядом ЛАХ відповідної розімкнутої системи. Виходячи з бажаного вигляду перехідного процесу, будують ЛАХ, яка відповідає такому процесу (бажану ЛАХ). Далі, знаючи вигляд бажаної ЛАХ, до неї наближують ЛАХ вихідної системи, використовуючі різні коректуючі пристрої.

Бажану ЛАХ, яка визначає потрібну якість системи, умовно поділяють на три частини: низькочастотну середньочастотну і високочастотну . Можливий вигляд бажаної ЛАХ показано на рис. 15.

До низькочастотної частини ЛАХ належить ділянка характеристики, нахил якої не змінюється при .

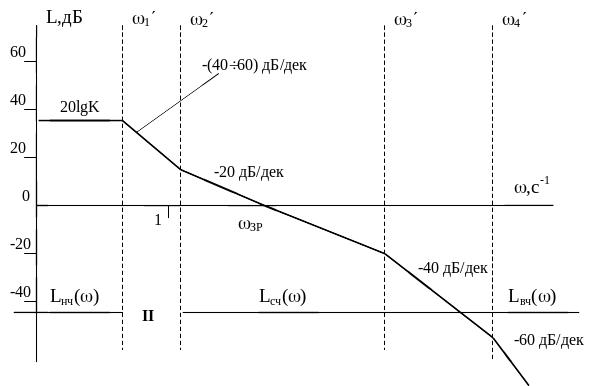
Рис. 15. Приклад бажаної ЛАХ

Низькочастотна частина ЛАХ визначається коефіцієнтом передачі розімкнутої системи К і порядком астатизму. Отже, вона характеризує точність роботи системи в усталених режимах. Якщо до незмінюваної частини системи належать елементи, що забезпечують потрібну точність роботи системи автоматичного регулювання в усталеному режимі, то низькочастотні частини бажаної ЛАХ і ЛАХ даної системи збігаються.

До середньочастотної частини належить ділянка ЛАХ з однаковим нахилом, що проходить через частоту зрізу . Ця частина ЛАХ є найважливішою, бо вона переважно визначає якість перехідних процесів. Основними параметрами, які характеризують середньочастотну частину, є її нахил і частота зрізу. Для задовільної якості перехідних процесів замкнутої системи необхідно, щоб нахил ЛАХ на частоті зрізу дорівнював -20 дБ/дек. Якщо нахил ЛАХ на частоті зрізу становить -40 дБ/дек, то перехідний процес має велике перерегулювання, а при нахилі – 60 дБ/дек система, як правило, буде нестійкою. Частота зрізу визначає швидкодію системи. Швидкодія зростає при збільшенні .

Високочастотна частина ЛАХ знаходиться в зоні від'ємних децибелів, тому майже не позначається на якості перехідного процесу і впливає лише на його початок. Власне кажучи, краще мати якомога більший нахил асимптот високочастотної частини, бо це зменшує вплив високочастотних перешкод. У деяких випадках високочастотну частину ЛАХ взагалі не беруть до уваги.

Послідовну коректуючу ланку вводять в основний контур регулювання системи. Вона звичайно є пасивним чотириполюсником або регулятором на базі операційного підсилювача. По можливості ланку слід вводити ближче до входу системи, де сигнали мають найменшу потужність. Передаточна функція послідовної коректуючої ланки знаходиться за формулою

де і - логарифмічні частотні характеристики бажаної і вихідної системи.

Ця формула визначає такий порядок синтезу корегуючої ланки:

• будують логарифмічну характеристику вихідної розімкнутої системи - ;

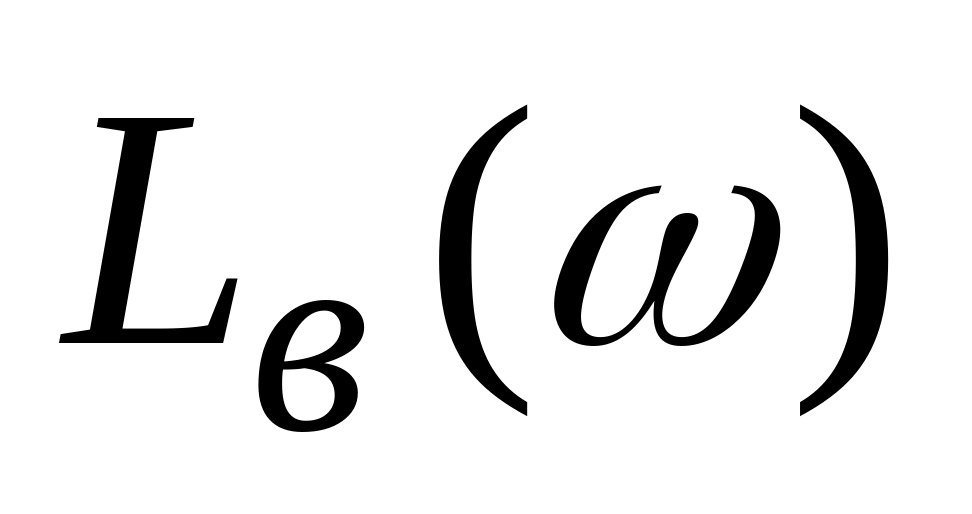• за заданими показниками якості будують бажану логарифмічну характеристику системи ;

• визначають логарифмічну характеристику корегуючої ланки 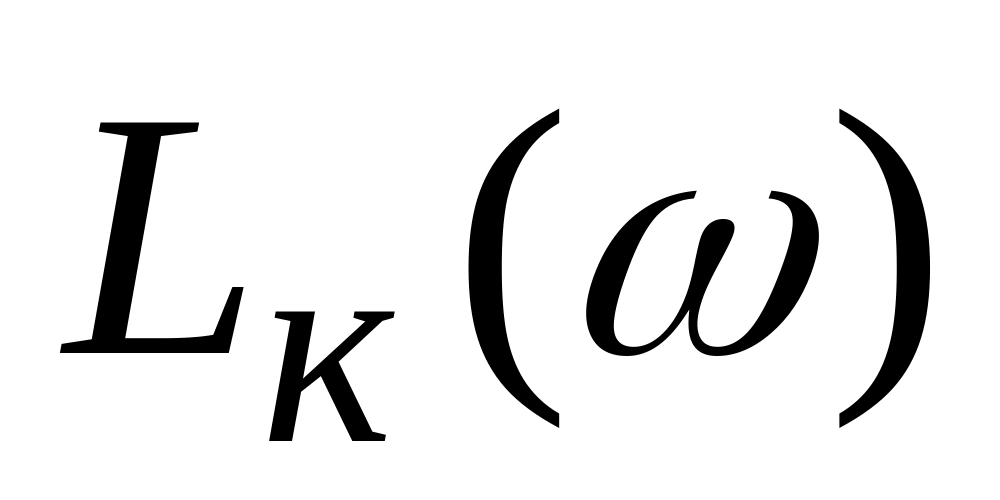як різницю характеристик - бажаної і вихідної;

• за логарифмічною характеристикою корегуючої ланки визначають її передаточну функцію і параметри.

Приклад. Запишемо передаточну функцію розімкненої системи у вигляді:

Запишемо амплітудну частотну характеристику для даної передаточної функції:

,

де - АЧХ аперіодичної ланки.

Запишемо вираз для амплітудної логарифмічної характеристики:

Знаходимо частоти спряження відповідно до сталих часу системи:

Гц;

Гц;

Гц

Нехай при відпрацюванні ступінчатого впливу тривалість перехідного процесу та перерегулювання не повинні перевищувати заданих значень:

t_p=2 c , _.

Знаходимо мінімальну величину частоти зрізу:

Для цього з номограми рис. 16. визначаємо m=2,4, яке беремо для заданого значення перерегулювання рівному 20%.

Гц.

Приймаємо частоту зрізу Гц.

Знаходимо значення амплітуди передаточної функції при =1, тобто 20lg(k):

20lgk=20*lg(37,3)=31,43.

Дана точка буде початковою.

Рис.16. Номограма для визначення частоти зрізу

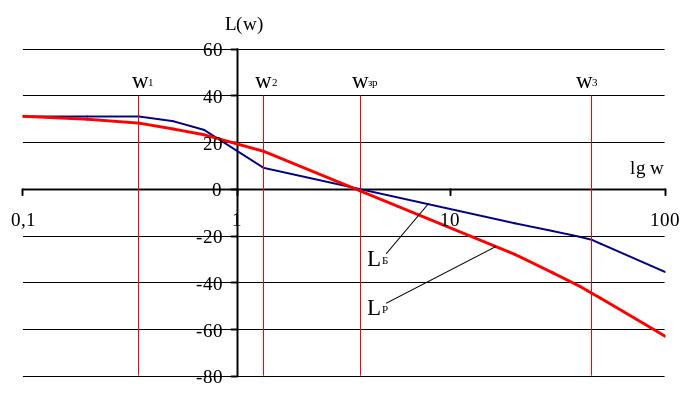
Рис. 17. Реальна і бажана ЛАЧХ

Рис. 18. ЛАЧХ коректуючої ланки

Як видно з ЛАЧХ коректуючої ланки, частота коректуючої ланки Гц.

Знаходимо сталу часу коректуючої ланки відповідно до частоти:

За даною логарифмічною характеристикою передаточна функція коректуючого пристрою буде мати вигляд:

Побудуємо схему та знімемо перехідну характеристику нашої системи, включивши послідовно коректуючу ланку.

Рис. 19. Структурна схема САР з коректуючою ланкою

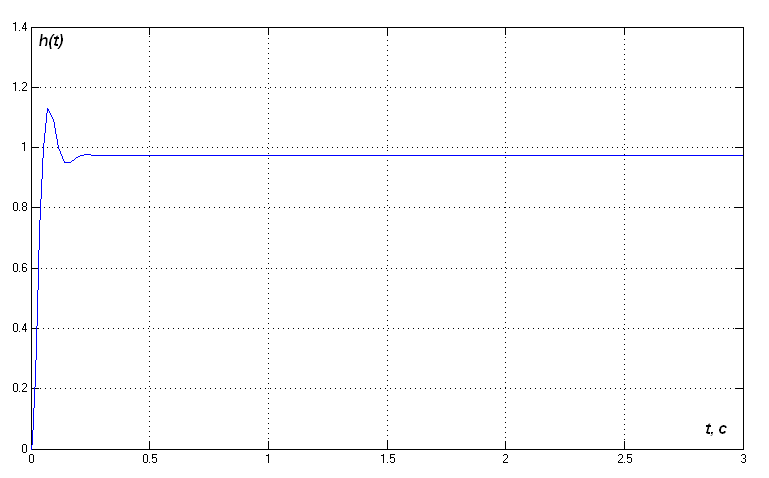
Рис. 20. Перехідна характеристика САР з послідовною коректуючою ланкою

Згідно з цією перехідною характеристикою знайдемо час регулювання t_p, величину перерегулювання σ та усталену похибку δ_уст:

t_p = 0.22 (с);

= =17%;

_уст=1 – h()=1 – 0.96=0.04.

Щоб усунути усталену помилку, введемо неодиничний зворотній зв’язок із коефіцієнтом передачі k_зз=1-1/k_р , де k_р - коефіцієнт передачі розімкнутої системи.

Рис. 21. Структурна схема скоректованої САР з неодиничним зворотним зв’язком

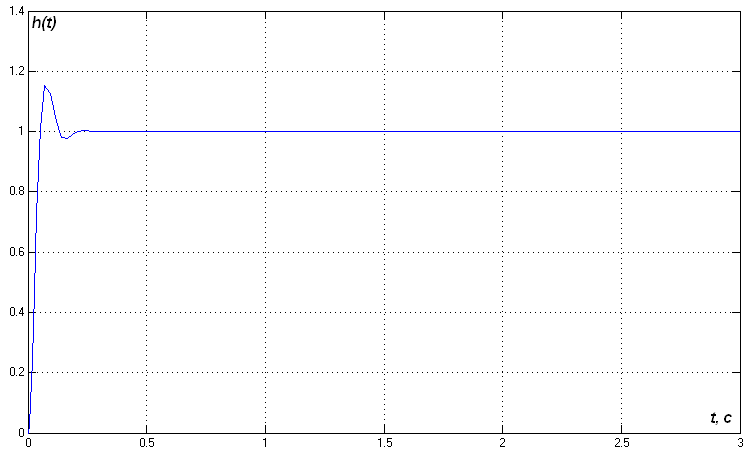
Рис. 22. Перехідна характеристика скоректованої САР з неодиничним зворотним зв’язком

Література

1. Теория автоматического управления: Учебник /Под ред. А.В. Нетушила - М.:Высшая школа, 1983. - 432 с.

2. Теория автоматического управления. Учебное пособие /Под ред. А.С. Шаталова - М.:Высшая школа, 1977. - 448 с.

3. Воронов А.А., Титов В.К., Новогренов Б.Н. Основы теории автоматического регулирования и управления: Учебное пособие. - М.:Высшая школа, 1977. - 519 с.

4. Попов Е.П. Теория нелинейных систем автоматического регулирования и управления: Учебное пособие. - М.:Наука, 1979. - 256 с.

5. Цыпкин Я.З. Основы теории автоматических систем: Учебное пособие. - М.:Наука, 1977. - 569 с.

6. М.Г.Попович, О.В.Ковальчук. Теорія автоматичного керування: Підручник.-Київ: Либідь, 1997.-525с.

7. Сборник задач по теории автоматического регулирования и управления/Под ред. В.А. Бесекерского - М.:Наука, 1979. - 512 с.

35