9. Розрахунок інтегральної квадратичної оцінки якості системи та визначення оптимального коефіцієнта підсилення регулятора
Інтегральні оцінки якості дають загальну оцінку швидкості затухання та відхилення регульованої величини в перехідному процесі.
Вони діляться на лінійні і квадратичні. До коливних затухаючих перехідних процесів можуть бути застосовані лише квадратичні інтегральні оцінки якості. Найпростіша квадратична оцінка якості керування є функціоналом від динамічної помилки системи і визначається за формулою
.
/23/
Динамічна похибка
виражає миттєве відхилення регульованої
величини від її усталеного значення
.
/24/
Інтегральна оцінка може бути виражена через зображення Лапласа від динамічної похибки системи
.
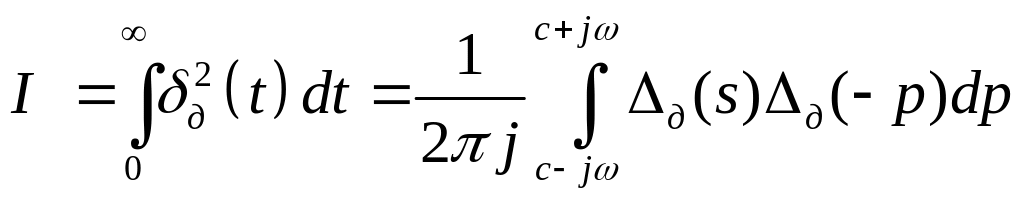/25/
Для визначення
квадратичної оцінки за зображенням
динамічної похибки на практиці
використовують формулу Рейлі, яку
отримують з /26/ шляхом заміни
.
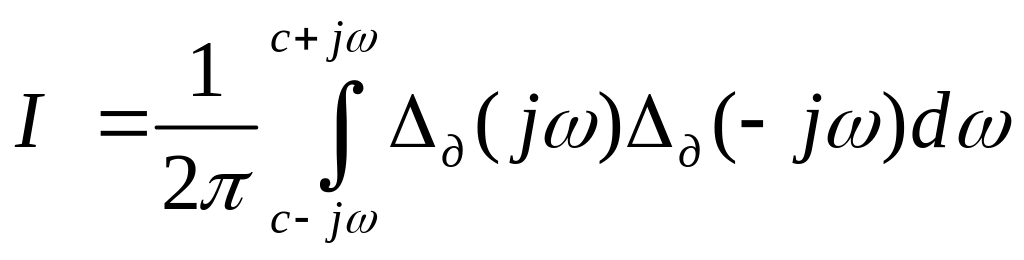/26/
Розроблені різні методи обчислення квадратичної оцінки на основі формули Рейлі. Зокрема, Мак–Леном отримані вирази для квадратичних оцінок якості керування для випадку, коли зображення динамічної похибки системи є дробово-раціональною функцією
/27/
- зі степенем полінома чисельника меншим на одиницю від степені полінома знаменника.
За методом Мак–Лена спочатку знаходять зображення динамічної похибки системи за формулою
,
/28/
- де
-
передаточна функція замкненої системи,
- зображення вхідної дії.
За виглядом зображення динамічної похибки вибирають вираз для визначення квадратичної оцінки якості. Якщо зображення динамічної похибки системи третього порядку має вигляд
,
/29/
то квадратичну оцінку якості знаходять за формулою
.
/30/
Інтегральні оцінки якості використовуються для знаходження оптимальних настроювальних параметрів системи. Наприклад, оптимальне значення коефіцієнта передачі регулятора kр при якому інтегральна оцінка якості приймає мінімальне значення знаходять з умови
.
/31/
Аналогічно можна знайти оптимальне значення іншого параметра при фіксованому значенні вже визначеного параметра.
Приклад. Розрахуємо інтегральну квадратичну оцінку якості системи. Запишемо передаточну функцію замкнутої системи:
.
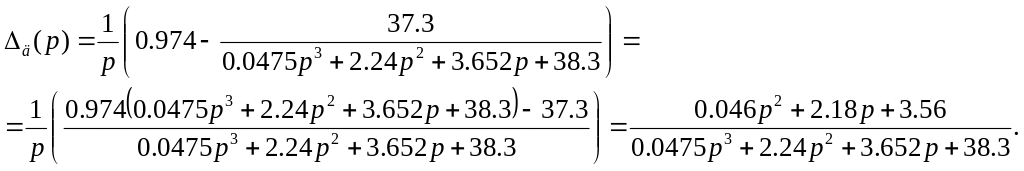Вираз
динамічної похибки є виразом третього
порядку , а отже для обчислення інтегральної
квадратичної оцінки якості застосуємо
формулу (32).
,
,
,
,
,
,
,
Знайдемо оптимальне значення коефіцієнта підсилення kп, для цього приймемо його за невідомий. В результаті отримаємо :
,
,
,
,
,
,
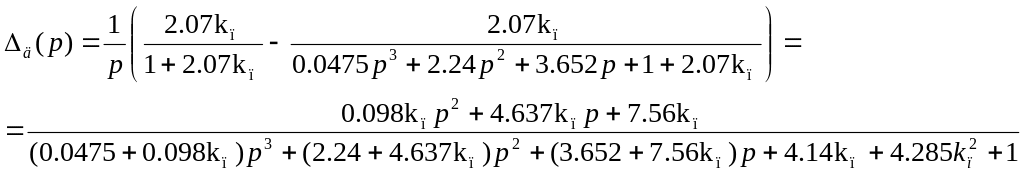
Визначимо частинну похідну скориставшись програмою Matlab:
>> c=[8.733 38.632 31.264 7.068 0 0];
>> z=[-0.035 28.884 70.131 68.044 32.986 7.987 0.773];
>> [p,r]=polyder(c,z)
p =
1.0e+003 *
0.0003 0.0027 -0.5001 -0.6166 0.6878 1.8363 1.5098 0.6189 0.1290 0.0109 0
r =
1.0e+004 *
0.0000 -0.0002 0.0829 0.4047 0.8847 1.1449 0.9718 0.5654 0.2283 0.0632 0.0115 0.0012 0.0001
де p – чисельник виразу частинної похідної
Прирівняємо чисельник отриманої похідної до 0 і знайдемо корені рівняння
cкориставшись Matlab :
>> m=roots(p)
m =
0
-44.5410
36.9120
1.6881
-0.5721 + 0.0636i
-0.5721 - 0.0636i
-0.4459 + 0.0951i
-0.4459 - 0.0951i
-0.4845
-0.3859
Отже оптимальні значення коефіцієнта передачі регулятора
kп1=1.688,
kп2=36.9120.
Для цих значень шляхом моделювання в ППП Маtlab Simulink побудуємо перехідні характеристики (рис.13, 14)
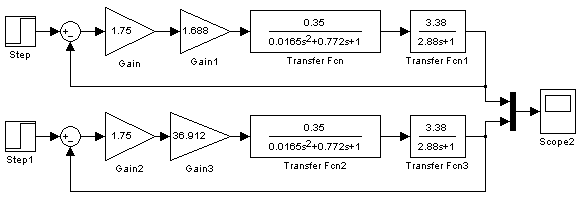
Рис.13. Simulink – модель САР температури
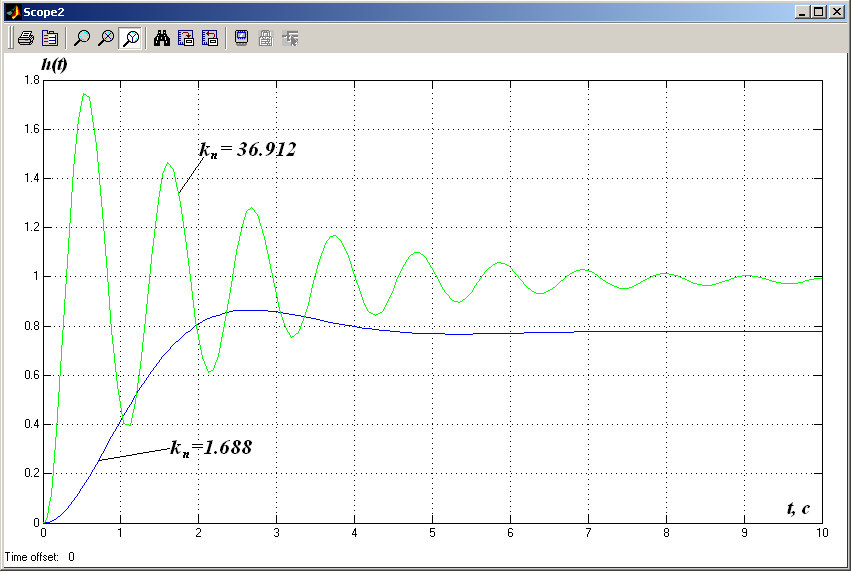
Рис. 14. Перехідні характеристики при різних значеннях коефіцієнтів передачі
Як бачимо перехідний процес в САР при kп1=1.688 має менше перерегулювання та час перехідного процесу, але при цьому в системі наявна усталена похибка. При kп2=36.9120 спостерігається коливний характер перехідного процесу та значне перерегулювання при відсутній усталеній похибці. Вибираємо коефіцієнт передачі kп1=1.688.