6. Розрахунок і побудова перехідної характеристики системи автоматичного керування

Аналітичні методи побудови перехідних характеристик ґрунтуються на розв’язку диференціального рівняння системи. Для цього може бути використаний як класичний метод розв’язку диференціальних рівнянь так і операторний, на основі зображень Лапласа. Основна складність класичного методу розв’язку диференціальних рівнянь полягає у визначенні сталих інтегрування і знаходження коренів характеристичного рівняння.

Найбільш поширеним методом розв’язку диференціальних рівнянь є операторний метод з використанням теореми розкладання. Операторний метод дає змогу уникнути трудомісткої процедури визначення сталих інтегрування і урахування початкових умов, але не звільняє від знаходження коренів характеристичного рівняння.

З численних способів визначення наближених значень коренів характеристичного рівняння ефективними є метод ділення многочленів та ітераційний метод. При виконанні роботи корені характеристичного рівняння рекомендується знаходити з допомогою комп’ютерної програми MatLab.

При операторному методі розв’язку диференціальних рівнянь спочатку знаходять зображення перехідної характеристики за формулою

, /12/

де - зображення Лапласа одиничної ступінчастої функції 1(t).

Операторний метод накладає обмеження на передаточну функцію замкнутої системи. Вона повинна бути дробово-раціональною, тобто представленою у вигляді відношення двох поліномів

. /13/

З урахуванням цього вираз для зображення перехідної характеристики можна привести до вигляду

. /14/

Згідно з теоремою розкладання для випадку одного нульового і некратних дійсних коренів характеристичного рівняння вираз для перехідної характеристики має вигляд

, /15/

де - корені характеристичного рівняння D(p) = 0; - похідна від полінома-знаменника передаточної функції.

У випадку комплексних коренів кожній парі комплексно-спряжених коренів

,

/16/

відповідають комплексні вирази

, , /17/

які мають однакові модулі, але різні знаки аргументів.

В результаті сума доданків, що відповідають парі комплексно-спряжених коренів, може бути зведена до одного виразу

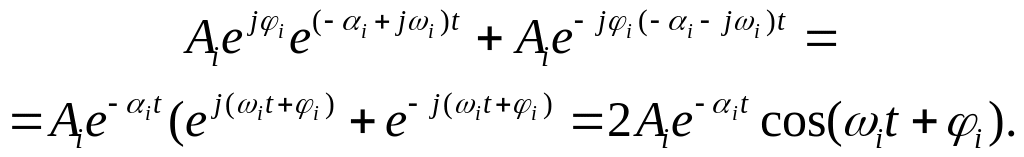. /18/

Таким чином у випадку k- дійсних і е - пар комплексних коренів теорему розкладання використовують у вигляді

. /19/

Приклад. Визначимо перехідну характеристику для системи автоматичного керування з передаточною функцією

. /20/

Згідно (12) для зображення перехідної характеристики отримаємо

/21/

Отже, у цьому випадку

,

,

.

Прирівнявши знаменник зображення передаточної функції до нуля отримуємо характеристичне рівняння замкнутої системи

. /22/

Скориставшись Matlab знайдемо корені характеристичного рівняння :

p₀= 0 с^-1,

p₁= -45,865 с^-1,

p₂= -0,64 + 4,142j с^-1,

p₃= -0,64 - 4,142j с^-1.

Підрахуємо:

,

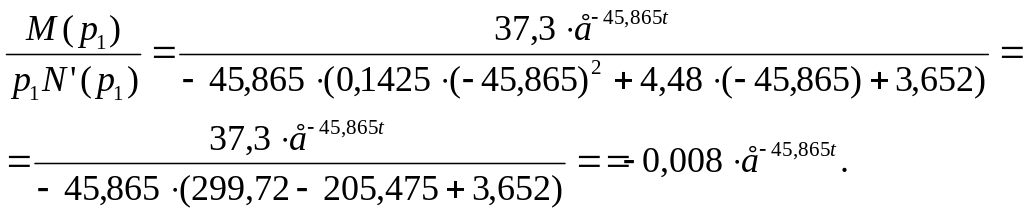
Відповідно

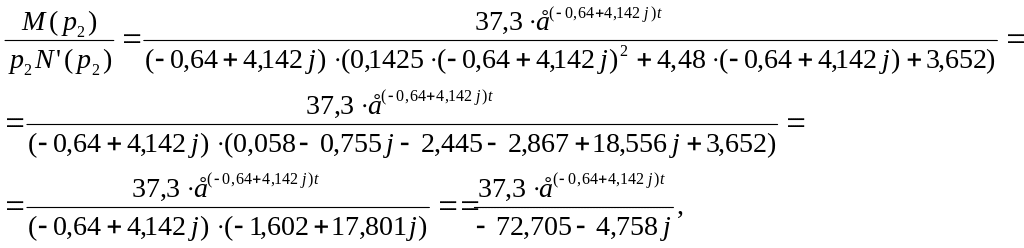
Аналогічно знаходимо

,

Скориставшись формулою Ейлера в результаті отримаємо

Запишемо рівняння перехідної характеристики:

.

За отриманою формулою розраховуємо перехідну характеристику замкнутої системи. Дані занесені у табл. 2.

Таблиця 2

t,c	0,00	0,30	0,45	0,76	1,06	1,52	1,67	1,97	2,58	3,03	3,64	4,09	4,55	5,00
h(t)	-0,03	0,67	1,16	1,59	1,16	0,60	0,68	1,04	1,05	0,83	1,05	1,00	0,92	0,98
t,c	5,61	6,06	6,52	7,12	7,58	8,03	8,48	9,09	9,55	10,00	10,61	11,06	11,52	12,12
h(t)	0,99	0,95	0,98	0,98	0,97	0,98	0,98	0,97	0,97	0,98	0,97	0,97	0,98	0,97

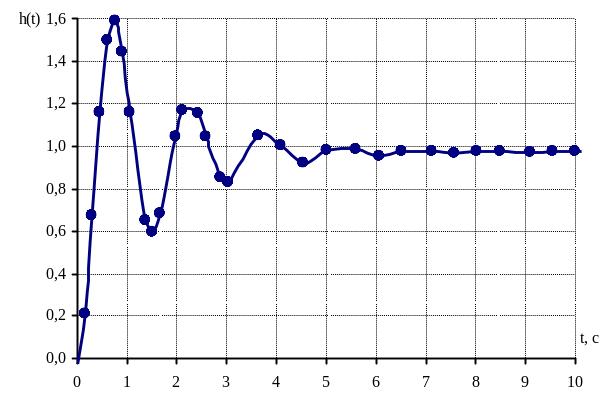
Рис.7. Перехідна характеристика САР за каналом задаючої дії

Аналогічним способом знаходять вираз для перехідної характеристики за каналом збурення. При цьому використовують передаточну функцію замкнутої системи за каналом збурення.