4. Аналіз стійкості системи та визначення критичного значення коефіцієнта передачі регулятора

При розробці і настроюванні систем автоматичного керування важливо встановити вплив окремих параметрів на їх стійкість. Для визначення областей допустимих значень параметрів можуть бути використані критерії стійкості та загальний метод D-розбиття.

Зокрема, критичне значення параметру (коефіцієнта передачі чи постійної часу ) при якому система знаходиться на межі області стійкості можна визначити за критерієм Гурвіца. Для цього необхідно прирівняти до нуля відповідний мінор визначника Гурвіца. У випадку системи третього порядку критичне значення параметру знаходять з розв’язку рівняння

/10/

Для визначення критичного значення параметру системи може бути використано частотний критерій Найквіста. За критерієм Найквіста система знаходиться на межі області стійкості, якщо годограф розімкнутої системи проходить через точку з координатами , тобто

/11/

У скалярній формі комплексне рівняння /11/ записують у вигляді системи рівнянь

Для визначення з другого рівняння визначають критичну частоту , при якій годограф характеристики пересікає дійсну від’ємну піввісь. Отримане значення підставляють в перше рівняння системи та знаходять значення .

Критичне значення досліджуваного параметру може бути визначене також із графічної побудови годографа частотної характеристики розімкнутої системи.

Приклад. Запишемо характеристичне рівняння системи, передаточна функція якої:

Складемо визначник Гурвіца для даного рівняння:

;

Головний визначник Гурвіца >0 і його мінори >0, >0, тому система з даними параметрами стійка.

Критичне значення коефіцієнта передачі підсилювача знайдемо, прийнявши його за невідомий у виразі та прирівнявши до нуля визначник Гурвіца:

Характеристичне рівняння замкнутої системи

Складемо мінор другого порядку визначника Гурвіца, оскільки він однозначно залежить від значення визначника Гурвіца

При критичному коефіцієнті передачі :

;

;

.

Отже, при система перебуватиме на межі стійкості.

5. Побудова годографа амплітудно-фазової частотної характеристики розімкнутої системи і визначення запасу стійкості

Побудову годографа амплітудно-фазової частотної характеристики розімкнутої системи ведуть в полярних, або декартових координатах. При побудові годографа частотної характеристики в полярних координатах спочатку знаходять вирази для амплітуди і фази кожної ланки окремо. Потім, для отримання виразів амплітудної і частотної характеристик системи, амплітуди ланок перемножують а фази сумують.

Стійкість системи автоматичного керування необхідно забезпечувати з певною гарантією – яка визначається запасом стійкості.

На комплексній площині коренів запас стійкості визначається віддаленістю коренів характеристичного рівняння від уявної вісі.

На основі алгебраїчних критеріїв запас стійкості системи можна оцінити за запасом, з яким виконуються нерівності.

Найчастіше оцінка запасу стійкості системи здійснюється на основі критерію Найквіста. При цьому розрізняють запас стійкості по модулю (амплітуді) і по фазі. Запас стійкості по амплітуді може бути визначений в абсолютних або відносних одиницях. Запас стійкості по модулю визначається відрізком осі абсцис між критичною точкою і точкою перетину годографа частотної характеристики розімкнутої системи з дійсною від’ємною піввіссю (рис. 5)

Рис. 5. Визначення запасу стійкості за частотними характеристиками системи

У відносних одиницях запас стійкості за модулем визначається відношенням

.

Запас стійкості за фазою визначається кутом між від’ємною піввіссю і променем проведеним з початку координат в точку перетину кола одиничного радіуса з годографом .

Для нормальної роботи системи автоматичного керування необхідно, щоб запас стійкості за модулем складав не менше 2 разів і за фазою - 30-60 градусів.

При використанні логарифмічних частотних характеристик запас стійкості за амплітудою визначається за характеристикою в точці переходу фазової характеристики через рівень -180 , а запас стійкості за фазою на основі характеристики в точці перетину характеристикою осі абсцис. Рекомендоване значення запасу стійкості за модулем у логарифмічному масштабі дБ.

Приклад. Для побудови годографа АФЧХ спочатку запишемо передаточну функцію розімкненої системи :

Виконавши заміну p=jω, отримаємо:

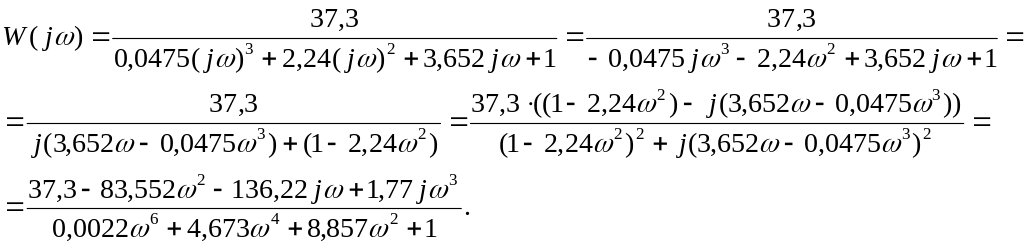
Для побудови годографа в декартовій системі координат виділимо дійсну та уявну частини W (jω) =P(ω) +jQ(ω):

;

.

Запаси стійкості визначимо, виходячи з критерію стійкості Найквіста. Для визначення запасу стійкості за амплітудою знайдемо частоту, яка відповідає точці перетину годографа АФЧХ з від'ємною дійсною піввіссю (з умови jQ( ) = 0):

Прирівняємо чисельник до нуля і знайдемо корені:

.

Тоді отримаємо

= 0, = 8.7727, = -8.7727.

Нас задовільняє лише значення = 8,7727. При цьому Q( ) = P(8,7727)=-0,218.

Запас стійкості за амплітудою А_зап= 1-0,218=0,782.

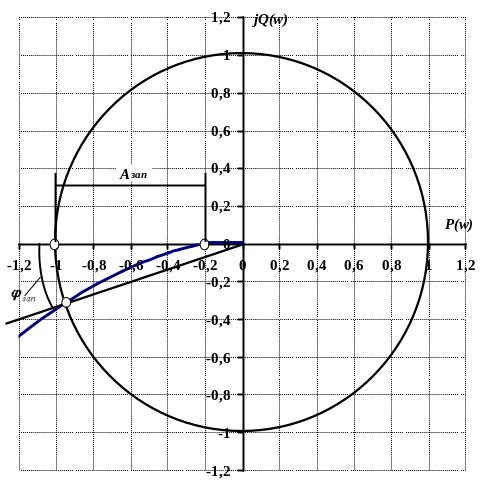
Рис. 6. Годограф АФЧХ та визначення запасів стійкості

З графіка видно, що точка перетину годографа системи із колом одиничного радіусу має координати (-0,94; -0,3).

.